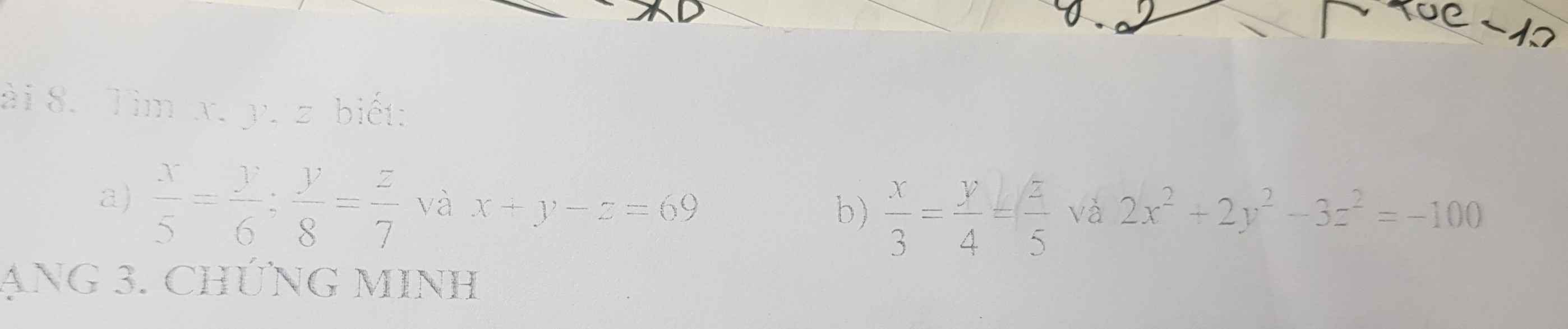 giúp e với ạ, e cảm ơn
giúp e với ạ, e cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x-y}{3-5}=\dfrac{22}{-2}=-11\Rightarrow x=-33;y=-55\)
b, \(\dfrac{5}{2}=\dfrac{y}{x}\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}\)Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=-\dfrac{21}{7}=-3\Rightarrow x=-6;y=-15\)
c, \(7x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{7}\)Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{x-y}{3-7}=-\dfrac{21}{-4}=7\Rightarrow x=28;y=49\)

Bài 11: \(\dfrac{2a+13b}{3a-7b}=\dfrac{2c+13d}{3c-7d}\)
=>\(\left(2a+13b\right)\left(3c-7d\right)=\left(3a-7b\right)\left(2c+13d\right)\)
=>\(6ac-14ad+39bc-91bd=6ac+39ad-14bc-91bd\)
=>-14ad-39ad=-14bc-39bc
=>ad=bc
=>\(\dfrac{a}{b}=\dfrac{c}{d}\)
Bài 12:
\(\dfrac{a+2019}{a-2019}=\dfrac{b+2020}{b-2020}\)
=>\(\left(a+2019\right)\left(b-2020\right)=\left(a-2019\right)\left(b+2020\right)\)
=>\(ab-2020a+2019b-2019\cdot2020=ab+2020a-2019b-2019\cdot2020\)
=>-2020a-2020a=-2019b-2019b
=>2020a=2019b
=>\(\dfrac{a}{2019}=\dfrac{b}{2020}\)

\(\left(x-4\right)^2\left(x+4\right)-\left(x-4\right)\left(x+4\right)^2+3\left(x^2-16\right)\)
\(=\left(x^2-16\right)\left(x-4\right)-\left(x^2-16\right)\left(x+4\right)+3\left(x^2-16\right)\)
\(=\left(x^2-16\right)\left(x-4-x-4+3\right)\)
\(=-5\left(x^2-16\right)=-5x^2+80\)

a: \(\dfrac{1}{2\text{x}5}+\dfrac{1}{5\text{x}8}+...+\dfrac{1}{14\text{x}17}\)
\(=\dfrac{1}{3}\text{x}\left(\dfrac{3}{2\text{x}5}+\dfrac{3}{5\text{x}8}+...+\dfrac{3}{14\text{x}17}\right)\)
\(=\dfrac{1}{3}\text{x}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+...+\dfrac{1}{14}-\dfrac{1}{17}\right)\)
\(=\dfrac{1}{3}\text{x}\left(\dfrac{1}{2}-\dfrac{1}{17}\right)=\dfrac{1}{3}\text{x}\dfrac{15}{34}=\dfrac{5}{34}\)
b: \(\dfrac{1}{1\text{x}5}+\dfrac{1}{5\text{x}9}+...+\dfrac{1}{17\text{x}21}\)
\(=\dfrac{1}{4}\text{x}\left(\dfrac{4}{1\text{x}5}+\dfrac{4}{5\text{x}9}+...+\dfrac{4}{17\text{x}21}\right)\)
\(=\dfrac{1}{4}\text{x}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{17}-\dfrac{1}{21}\right)\)
\(=\dfrac{1}{4}\text{x}\left(1-\dfrac{1}{21}\right)=\dfrac{1}{4}\text{x}\dfrac{20}{21}=\dfrac{5}{21}\)

\(\left(2x+1\right)\left(4x^2-2x+1\right)-\left(2x-1\right)\left(4x^2+2x+1\right)\)
\(=8x^3+1-\left(8x^3-1\right)=8x^3+1-8x^3+1=2\)

\(\left(x+3\right)\left(x^2-3x+9\right)=28\)
=>\(x^3+27=28\)
=>\(x^3=1=1^3\)
=>x=1

\(\dfrac{2020^3+1}{2020^2-2019}=\dfrac{\left(2020+1\right)\left(2020^2-2020\cdot1+1\right)}{2020^2-2019}\)
\(=\dfrac{2021\cdot\left(2020^2-2019\right)}{2020^2-2019}\)
=2021

a: \(2\cdot5^2+3:71^0-54:3^3\)
\(=2\cdot25+3:1-54:27\)
=50+3-2=51
b: \(36\cdot4-4\cdot\left(82-7\cdot11\right)^2:4-2016^0\)
\(=144-\left(82-77\right)^2-1\)
\(=143-5^2=143-25=118\)

Sửa đề: \(\dfrac{2020^3-1}{2020^2+2021}\)
\(=\dfrac{\left(2020-1\right)\left(2020^2+2020+1\right)}{2020^2+2020+1}\)
=2020-1=2019
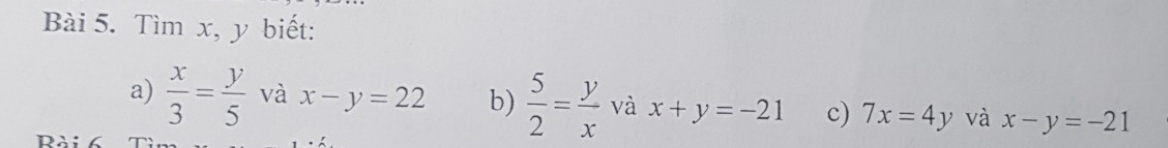
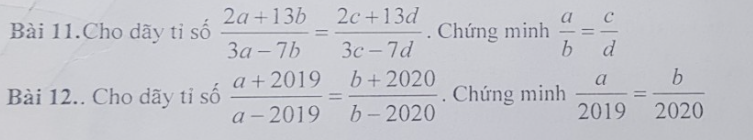
Bài 8:
a: \(\dfrac{x}{5}=\dfrac{y}{6}\)
=>\(\dfrac{x}{20}=\dfrac{y}{24}\)
\(\dfrac{y}{8}=\dfrac{z}{7}\)
=>\(\dfrac{y}{24}=\dfrac{z}{21}\)
Do đó: \(\dfrac{x}{20}=\dfrac{y}{24}=\dfrac{z}{21}=k\)
=>x=20k;y=24k;z=21k
x+y-z=69
=>20k+24k-21k=69
=>23k=69
=>k=3
=>\(x=20\cdot3=60;y=24\cdot3=72;z=21\cdot3=63\)
b: Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=k\)
=>x=3k;y=4k;z=5k
\(2x^2+2y^2-3z^2=-100\)
=>\(2\cdot\left(3k\right)^2+2\cdot\left(4k\right)^2-3\cdot\left(5k\right)^2=-100\)
=>\(k^2=4\)
=>\(\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\)
TH1: k=2
=>\(x=3\cdot2=6;y=4\cdot2=8;z=5\cdot2=10\)
TH2: k=-2
=>\(x=3\cdot\left(-2\right)=-6;y=4\cdot\left(-2\right)=-8;z=5\cdot\left(-2\right)=-10\)