Diện tích đáy bể là:

\(45\cdot25=1125\left(m^2\right)\)

Chiều cao của bể là:

\(2250:1125=2\left(m\right)\)

Đáp số: 2 m

\(\dfrac{1}{3\times5}+\dfrac{1}{5\times7}+\dfrac{1}{7\times9}+...+\dfrac{1}{25\times27}\)

\(=\dfrac{1}{2}\times\left(\dfrac{1}{3\times5}+\dfrac{1}{5\times7}+\dfrac{1}{7\times9}+...+\dfrac{1}{25\times27}\right)\)

\(=\dfrac{1}{2}\times\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{25}-\dfrac{1}{27}\right)\)

\(=\dfrac{1}{2}\times\left(\dfrac{1}{3}-\dfrac{1}{27}\right)\)

\(=\dfrac{1}{2}\times\dfrac{8}{27}\)

\(=1\times\dfrac{4}{27}=\dfrac{4}{27}\)

\(\dfrac{1}{3\text{x}5}+\dfrac{1}{5\text{x}7}+...+\dfrac{1}{25\text{x}27}\)

\(=\dfrac{1}{2}\text{x}\left(\dfrac{2}{3\text{x}5}+\dfrac{2}{5\text{x}7}+...+\dfrac{2}{25\text{x}27}\right)\)

\(=\dfrac{1}{2}\text{x}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{25}-\dfrac{1}{27}\right)\)

\(=\dfrac{1}{2}\text{x}\left(\dfrac{1}{3}-\dfrac{1}{27}\right)=\dfrac{1}{2}\text{x}\dfrac{8}{27}=\dfrac{4}{27}\)

a: \(\left(ac+bd\right)^2+\left(ad-bc\right)^2\)

\(=a^2c^2+b^2d^2+2acbd+a^2d^2+b^2c^2-2adbc\)

\(=a^2c^2+a^2d^2+b^2d^2+b^2c^2\)

\(=a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\)

\(=\left(c^2+d^2\right)\left(a^2+b^2\right)\)

b: \(x^2+y^2=\dfrac{1}{2}\left(2x^2+2y^2\right)\)

\(=\dfrac{1}{2}\left(x^2+2xy+y^2+x^2-2xy+y^2\right)\)

\(=\dfrac{1}{2}\left[\left(x+y\right)^2+\left(x-y\right)^2\right]=\dfrac{1}{2}\left[4+\left(x-y\right)^2\right]>=\dfrac{1}{2}\cdot4=2\)

Dấu '=' xảy ra khi x=y=1

Giá tiền vốn của 20 xe đạp là:

\(1600000:8\%=20000000\left(đ\right)\)

Cửa hàng bán 1 xe đạp giá:

\(20000000:20=2000000\left(đ\right)\)

Đáp số: 2 000 000 đồng

ED lam sai roi

a: \(CN=\dfrac{2}{3}CA\)

=>\(S_{BNC}=\dfrac{2}{3}\times S_{ABC}=\dfrac{2}{3}\times216=144\left(cm^2\right)\)

=>\(S_{ABN}=216-144=72\left(cm^2\right)\)

Vì BM=2/3BA

nên \(AM=\dfrac{1}{3}AB\)

=>\(S_{AMN}=\dfrac{1}{3}\times S_{ABN}=24\left(cm^2\right)\)

b: Vì BI=2/3BC

nên \(CI=\dfrac{1}{3}CB\)

=>\(S_{CIN}=\dfrac{1}{3}\times S_{NBC}=\dfrac{1}{3}\times144=48\left(cm^2\right)\)

\(S_{AMN}+S_{BMNI}+S_{NIC}=S_{ABC}\)

=>\(S_{BMNI}+48+24=216\)

=>\(S_{BMNI}=144\left(cm^2\right)\)

hình đâu

khi ta chuyển dấu phảy của số đó sang trái hai chữ số thì số đó sẽ giảm đi 100 lần. Vậy, t có sơ đồ:

số cũ: 100 phần

số mới: 1 phần

hiệu: 200,376

số cần tìm là: 200,376: (100-1)x 100= 202,4

đáp số: 202,4

khi ta chuyển dấu phảy của số đó sang trái hai chữ số thì số đó sẽ giảm đi 100 lần. Vậy, t có sơ đồ:

số cũ: 100 phần

số mới: 1 phần

hiệu: 200,376

số cần tìm là: 200,376: (100-1)x 100= 202,4

đáp số: 202,4

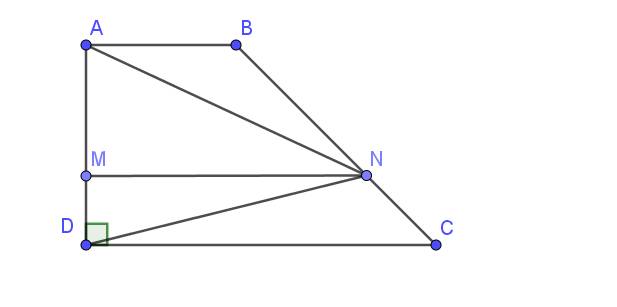
Lời giải:

$S_{ABCD}=(AB+CD)\times AD:2=(20+40)\times 25:2=750$ (m²)

$S_{ABN}=AM\times AB:2=(AD-MD)\times AB:2=(25-8)\times 20:2=170$ (m²)

$S_{CDN}=CD\times MD:2=40\times 8:2=160$ (m²)

$S_{ADN}=MN\times AD:2=S_{ABCD}-S_{ABN}-S_{CDN}$

$MN\times 25:2=750-170-160$

$MN\times 25:2=420$

$MN=420\times 2:25=33,6$ (m)

$S_{ABNM}=(AB+MN)\times AM:2=(20+33,6)\times (25-8):2=455,6$ (m²)

Hình vẽ:

Làm gì có tháng 13 đâu nhỉ?

1 năm có 12 tháng thôi em nhé!

Không có tháng 13 đâu!

1: Thay x=2 vào phương trình, ta được:

\(2^2-2\left(m-2\right)\cdot2+m^2-8=0\)

=>\(4-4\left(m-2\right)+m^2-8=0\)

=>\(4-4m+8+m^2-8=0\)

=>\(m^2-4m+4=0\)

=>\(\left(m-2\right)^2=0\)

=>m-2=0

=>m=2