Cho hai số có tổng bằng 32 và hai số đó tỉ lệ với 3 và 5.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Góc IA = góc IE làm sao được em. Góc thì phải có 3 đỉnh chứ sao mỗi góc ở đây có hai đỉnh vậy em

a) x và y là hai đại lượng tỉ lệ nghịch theo hệ số a nên:
`a=y/x=4/2=2`
b) Ta có: `a=2`
`=>y/x=2=>y=2x`
c) khi `y=-1=>2x=-1=>x=-1/2`
Khi `y=2=>2x=2=>x=1`

Lời giải:
a. Xét tam giác $BAD$ và $BHD$ có:
$\widehat{BAD}=\widehat{BHD}=90^0$
$BD$ chung
$\widehat{ABD}=\widehat{HBD}$ (do $BD$ là phân giác $\widehat{B}$)
$\Rightarrow \triangle BAD=\triangle BHD$ (ch-gn)
$\Rightarrow AB=BH$
b. Từ tam giác bằng nhau phần a suy ra $AD=DH$ (1)
Xét tam giác vuông $DHC$ vuông tại $H$ nên $DC> DH$ (do $DC$ là cạnh huyền) (2)
Từ $(1); (2)\Rightarrow DC> AD$
c.
Xét tam giác $BIH$ và $BCA$ có:
$\widehat{B}$ chung
$BH=BA$ (cmt)
$\widehat{BHI}=\widehat{BAC}=90^0$
$\Rightarrow \triangle BIH=\triangle BCA$ (g.c.g)
$\Rightarrow BI=BC$
$\Rightarrow BIC$ cân tại $I$

Lời giải:
Xét tam giác $BAM$ và $CDM$ có:
$BM=CM$
$AM=DM$
$\widehat{BMA}=\widehat{CMD}$ (đối đỉnh)
$\Rightarrow \triangle BAM=\triangle CDM$ (c.g.c)
$\Rightarrow AB=CD$ và $\widehat{BAM}=\widehat{CDM}$
Mà 2 góc này ở vị trí so le trong nên $AB\parallel CD$
$AB\perp AC$ nên $CD\perp AC\Rightarrow \widehat{DCA}=90^0$
Xét tam giác $BAC$ và $DCA$ có:
$\widehat{BAC}=\widehat{DCA}=90^0$
$BA=CD$ (cmt)
$AC$ chung
$\Rightarrow \triangle BAC=\triangle DCA$ (c.g.c)
$\Rightarrow BC=DA$
$\Rightarrow BC:2=DA:2\Rightarrow BM=AM$
$\Rightarrow MBA$ cân tại $M\Rightarrow \widehat{MBA}=\widehat{MAB}$
Hay $\widehat{ABC}=\widehat{BAD}$

Đặt \(\dfrac{a+b}{3}=\dfrac{b+c}{4}=\dfrac{c+a}{5}=t\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=3t\\b+c=4t\\c+a=5t\end{matrix}\right.\)
\(\Rightarrow\left(a+b\right)+\left(b+c\right)+\left(c+a\right)=3t+4t+5t\)
\(\Leftrightarrow2\left(a+b+c\right)=12t\)
\(\Leftrightarrow a+b+c=6t\)
+ \(\left\{{}\begin{matrix}a+b=3t\\a+b+c=6t\end{matrix}\right.\) \(\Rightarrow3t+c=6t\) \(\Leftrightarrow c=3t\)
+ \(\left\{{}\begin{matrix}b+c=4t\\a+b+c=6t\end{matrix}\right.\) \(\Rightarrow a+4t=6t\) \(\Leftrightarrow a=2t\)
+ \(\left\{{}\begin{matrix}c+a=5t\\a+b+c=6t\end{matrix}\right.\) \(\Rightarrow b+5t=6t\) \(\Leftrightarrow b=t\)
Thay \(a=2t;b=t;c=3t\) vào \(M\) ta được
\(M=10\cdot2t+t-7\cdot3t+2017=20t+t-21t+2017=2017\)
Vậy \(M=2017\)

Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{3x-2y}{4}=\dfrac{4y-3z}{2}=\dfrac{2z-4x}{3}=\dfrac{12x-8y}{16}=\dfrac{8y-6z}{4}\)
\(=\dfrac{6z-12x}{9}=\dfrac{12x-8y+8y-6z+6z-12x}{16+4+9}=0\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{3x-2y}{4}=0\\\dfrac{4y-3z}{2}=0\\\dfrac{2z-4x}{3}=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}3x=2y\\4y=3z\\2z=4x\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}\\\dfrac{y}{3}=\dfrac{z}{4}\\\dfrac{z}{4}=\dfrac{x}{2}\end{matrix}\right.\)
\(\Rightarrow\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{2y}{6}=\dfrac{3z}{12}=\dfrac{x-2y+3z}{2-6+12}=\dfrac{8}{8}=1\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.1=2\\y=3.1=3\\z=4.1=4\end{matrix}\right.\)
Ta có: \(\dfrac{3x-2y}{4}=\dfrac{4y-3z}{2}=\dfrac{2z-4x}{3}\)
hay \(\dfrac{12x-8y}{16}=\dfrac{8y-6z}{4}=\dfrac{6z-12x}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{12x-8y}{16}=\dfrac{8y-6z}{4}=\dfrac{6z-12x}{9}=\dfrac{12x-8y+8y-6z+6z-12x}{16+4+9}=\dfrac{0}{29}=0\)
Do đó:
\(\dfrac{3x-2y}{4}=0\Rightarrow3x=2y\Rightarrow\dfrac{x}{2}=\dfrac{y}{3}\left(1\right)\)
\(\dfrac{4y-3z}{2}=0\Rightarrow4y=3z\Rightarrow\dfrac{y}{3}=\dfrac{z}{4}\left(2\right)\)
\(\dfrac{2z-4x}{3}=0\Rightarrow2z=4x\Rightarrow\dfrac{z}{4}=\dfrac{x}{2}\left(3\right)\)
Từ (1), (2) và (3) suy ra: \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\Rightarrow\dfrac{x}{2}=\dfrac{2y}{6}=\dfrac{3z}{12}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{2}=\dfrac{2y}{6}=\dfrac{3z}{12}=\dfrac{x-2y+3z}{2-6+12}=\dfrac{8}{8}=1\)
Do đó:
\(\dfrac{x}{2}=1\Rightarrow x=2.1=2\)
\(\dfrac{y}{3}=1\Rightarrow y=3.1=3\)
\(\dfrac{z}{4}=1\Rightarrow z=4.1=4\)
Vậy x = 2; y = 3; z = 4.
\(#NqHahh\)

Lời giải:
Theo bài ra ta có:
$\frac{x}{3}=\frac{y}{5}; \frac{y}{4}=\frac{z}{5}$
$\Rightarrow \frac{x}{12}=\frac{y}{20}=\frac{z}{25}$
Áp dụng TCDTSBN:
$\frac{x}{12}=\frac{y}{20}=\frac{z}{25}=\frac{x+y+z}{12+20+25}=\frac{456}{57}=8$
$\Rightarrow x=12.8=96; y=20.8=160; z=25.8=200$
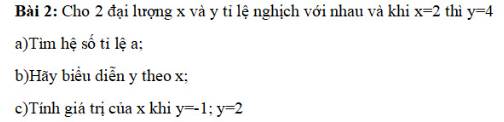

Gọi hai số cần tìm là a,b
Hai số tỉ lệ với 3 và 5 nên \(\dfrac{a}{3}=\dfrac{b}{5}\)
Tổng hai số là 32 nên a+b=32
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{a+b}{3+5}=\dfrac{32}{8}=4\)
=>\(a=4\cdot3=12;b=4\cdot5=20\)