Quãng đường AB dài 120km. Một người đi xe máy từ A đến B với vận tốc 60km/h, sau đó người này dừng nghỉ 15 phút rồi quay trở về A với vận tốc 50km/h.
Tính vận tốc trung bình của xe khi đi và quay về ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cấu tạo của hệ bạch huyết gồm:
Phân hệ lớn:
- Mao mạch bạch huyết
- Hạch bạch huyết
- Mạch bạch huyết
- Ống bạch huyết
Phân hệ nhỏ:
- Mao mạch bạch huyết
- Hạch bạch huyết
- Mạch bạch huyết
- Ống bạch huyết
Nó bao gồm bạch huyết, mạch bạch huyết, mô bạch huyết, hạt/mấu bạch huyết, hạch bạch huyết, hạch họng, lá lách, và tuyến ức. Hệ bạch huyết được hai người Olaus Rudbeck và Thomas Bartholin độc lập với nhau mô tả lần đầu tiên vào thế kỷ 17. Không giống như hệ tuần hoàn, hệ bạch huyết không phải là một hệ thống đóng.

Lời giải:
a.
\(x=\frac{b^2-a^2}{a^2}: \frac{a^3-b^3}{a^4}=\frac{(b-a)(b+a)}{a^2}.\frac{a^4}{(a-b)(a^2+ab+b^2)}=\frac{-a^2(a+b)}{a^2+ab+b^2}\)
b.
\(x=\frac{a-b}{a^3+b^3}: \frac{a^2+b^2-2ab}{a^2+b^2-ab}=\frac{a-b}{(a+b)(a^2-ab+b^2)}: \frac{(a-b)^2}{a^2-ab+b^2}\)
\(x=\frac{a-b}{(a+b)(a^2-ab+b^2)}.\frac{a^2-ab+b^2}{(a-b)^2}=\frac{1}{(a+b)(a-b)}=\frac{1}{a^2-b^2}\)

Lời giải:
$\frac{1}{x}-\frac{1}{y}-\frac{1}{z}=0$
$\Leftrightarrow \frac{yz}{xyz}-\frac{xz}{xyz}-\frac{xy}{xyz}=0$
$\Leftrightarrow \frac{yz-xz-xy}{xyz}=0$
$\Leftrightarrow yz-xz-xy=0$
Đây mới đúng nhé bạn. Đoạn biểu thức sau "chứng minh" của bạn có lẽ bị viết sai rồi.

Để phân số $\frac{a}{b}$ có nghĩa thì $b\neq 0$
a.
ĐKXĐ: \(\left\{\begin{matrix} 3x-3\neq 0\\ 4-4x\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3(x-1)\neq 0\\ -4(x-1)\neq 0\end{matrix}\right.\Leftrightarrow x-1\neq 0\Leftrightarrow x\neq 1\)
b.
ĐKXĐ: \(\left\{\begin{matrix} a+3\neq 0\\ 3a^2+14a+15\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a+3\neq 0\\ (3a+5)(a+3)\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3a+5\neq 0\\ a+3\neq 0\end{matrix}\right.\Leftrightarrow a\neq \frac{-5}{3}; a\neq -3\)
c.
ĐKXĐ: \(\left\{\begin{matrix} b^3+1\neq 0\\ b^2-b+1\neq 0\\ b+1\neq 0\end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b^3+1\neq 0\\ (b+1)(b^2-b+1)\neq 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} b^3+1\neq 0\\ b^3+1\neq 0\end{matrix}\right.\Leftrightarrow b^3\neq -1\Leftrightarrow b\neq -1\)
e.
ĐKXĐ: \(\left\{\begin{matrix} 4x^2-2xy\neq 0\\ 2y^2-4xy\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2x(2x-y)\neq 0\\ 2y(y-2x)\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 0\\ 2x-y\neq 0\\ y-2x\neq 0\\ y\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 0\\ x\neq \frac{y}{2}\\ y\neq 0\\ \end{matrix}\right.\)
h.
ĐKXĐ: \(\left\{\begin{matrix} x-5\neq 0\\ x+5\neq 0\\ 25-x^2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x-5\neq 0\\\ x+5\neq 0\\ -(x-5)(x+5)\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x-5\neq 0\\ x+5\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 5\\ x\neq -5\end{matrix}\right.\)
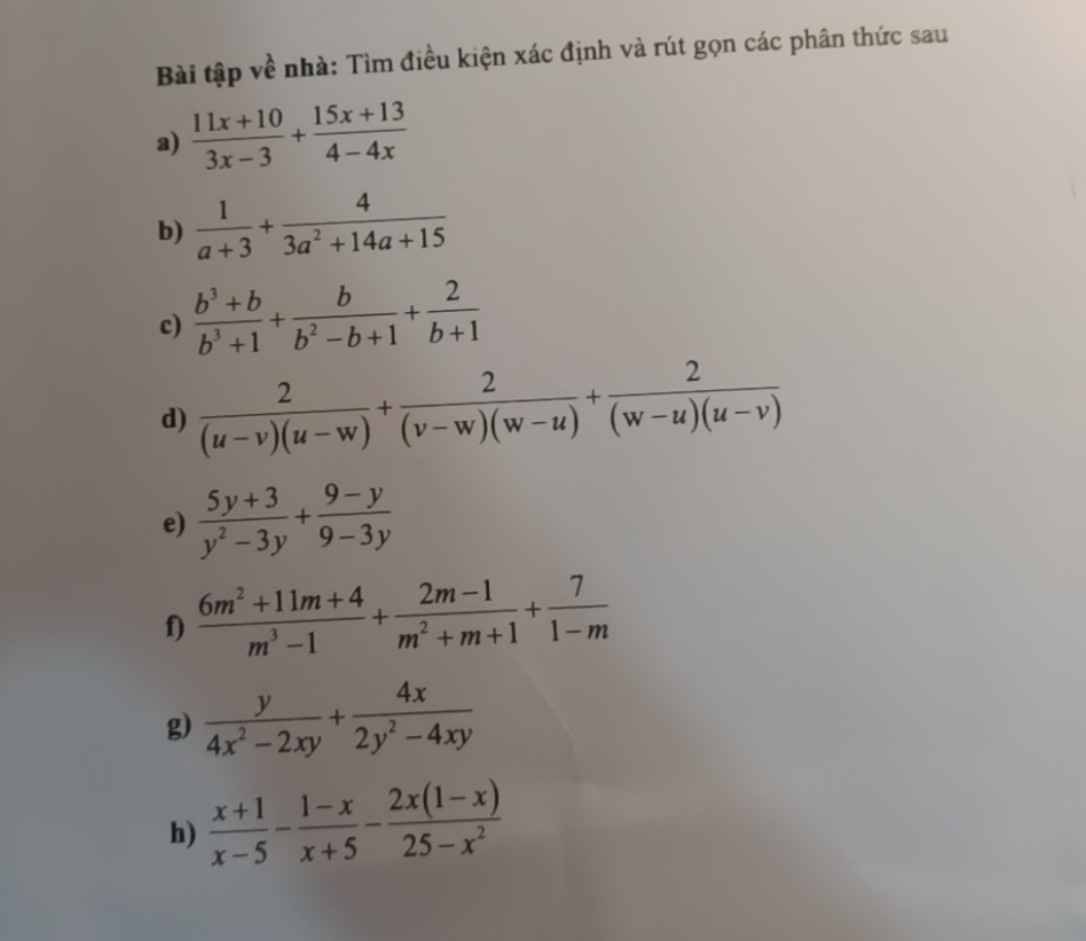
Thời gian xe lúc đi: \(t_1=\dfrac{S}{v_1}=\dfrac{120}{60}=2h\)
Thời gian xe lúc về: \(t_2=\dfrac{S}{v_2}=\dfrac{120}{50}=2,4h\)
Thời gian nghỉ: \(t_{nghỉ}=\dfrac{15}{60}=\dfrac{1}{4}h\)
Vận tốc trung bình trên cả quãng đường đi và về:
\(v_{tb}=\dfrac{120+120}{2+2,4+\dfrac{1}{4}}=51,6km/h\)