Cho tam giác ABC có 3 góc nhọn. Vẽ các đường cao BD, CE. Gọi K,H lần lượt là hình chiếu vuông góc với E lên AC và BD. Chứng minh AE×DK= AK×EB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sự phát triển của kinh tế hàng hoá đã tạo điều kiện thuận lợi cho sự hình thành và hưng khởi của đô thị.
Vào các thế kỉ XVI – XVIII, nhiều đô thị mới hình thành ở miền Bắc và miền Nam. Khu cư dân Thăng Long cũng phát triển với tên Kẻ Chợ gồm 36 phố phường và 8 chợ.
Một thương nhân nước ngoài đã mô tả : “Các phố ở Kẻ Chợ đều rộng, đẹp và lát gạch từng phần...” Một thương nhân khác nói thêm : “Tất cả những vật phẩm khác nhau bán trong thành phố này đều được dành riêng cho từng phường...”
Phố Hiến (phía nam thị xã Hưng Yên ngày nay) ra đời và phát triển phồn thịnh. Nhân dân có câu ‘Thứ nhất Kinh Kì, thứ nhì Phố Hiến ”. Theo người phương Tây mô tả, bấy giờ Phố Hiến có khoảng 2000 nóc nhà.
Hội An là thành phố cảng lớn nhất ở Đàng Trong (trên đất Quảng Nam ngày nay), phát triển chủ yếu ở các thế kỉ XVII - XVIII.
Giáo sĩ Bo-ri đã viết : “Hải cảng đẹp nhất, nơi mà thương nhân ngoại quốc thường lui tới buôn bán là hải cảng thuộc tỉnh Các-ci-am (Quảng Nam)... Thành phố đó lớn lắm, đến nỗi người ta có thể nói nó có 2 thị trấn, một của người Trung Quốc và một của người Nhật Bản.” (Tường trình về vương quốc Đàng Trong)
Thanh Hà cũng là một đô thị mới hình thành ở trên bờ sông Hương, gần Phú Xuân (Huế) do các thương nhân Trung Hoa thành lập với sự đồng ý cùa chúa Nguyễn. Trao đổi buôn bán ở đây khá sầm uất và người đương thời đã gọi là “Đại Minh khách phố”.
Ngoài ra, còn có một số trung tâm buôn bán nhỏ hơn, phồn vinh một thời.
Vào đầu thế kỉ XIX, do nhiều nguyên nhân khác nhau, các đó thị suy tàn dần, thậm chí không còn được nhắc đến, trừ Thăng Long.

Để khẳng định chủ quyền độc lập của dân tộc, Nguyễn Trãi đã dựa vào các yếu tố như: nền văn hiến lâu đời, cương vực lãnh thổ, phong tục tập quán, lịch sử riêng, chế độ riêng. Với những yếu tố căn bản này, tác giả đã đưa ra một khái niệm khá hoàn chỉnh về quốc gia, dân tộc.
So với ý thức về quốc gia dân tộc trong bài thơ Sông núi nước Nam, thì ở Nguyễn Trãi, ta thấy nó vừa có sự kế thừa lại vừa có sự phát huy và hoàn thiện. Ý thức về nền độc lập của dân tộc thể hiện trong bài Sông núi nước Nam được xác định ở hai phương diện: lãnh thổ và chủ quyền; còn trong bài Nước Đại Việt ta, ý thức dân tộc đã phát triển cao, sâu sắc và toàn diện. Ngoài lãnh thổ và chủ quyền, ý thức về độc lập dân tộc còn được mở rộng, bổ sung thành các yếu tố mới: đó là nền văn hiến lâu đời, đó là phong tục tập quán riêng, truyền thống lịch sử anh hùng. Có thể nói, ý thức dân tộc đến thế kỉ XV đã phát triển sâu sắc, toàn diện hơn nhiều so với thế kỉ X.
Trả lời
Bạn xem tại link này:
Câu hỏi của Quỳnh Luna - Ngữ văn lớp 8 | Học trực tuyến
~ Mik ko biết có bại lạc đề không?~

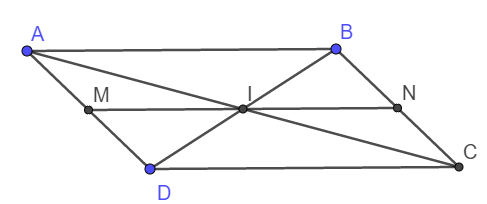
1. Xét tam giác ABD có MI // AB nên theo định lý Talet ta có:
\(\frac{MI}{AB}=\frac{DI}{DB}\)
Xét tam giác ABC có NI // AB nên theo định lý Talet ta có:
\(\frac{NI}{AB}=\frac{NC}{BC}\)
2. Xét tam giác BDC có IN // DC nên \(\frac{DI}{DB}=\frac{NC}{BC}\)
Từ đó ta có: \(\frac{MI}{AB}=\frac{NI}{AB}\Rightarrow MI=IN\)
Vậy I là trung điểm MN (đpcm)

ọi phương trình là A
A <=> 4x^6 + 4x^5 + 4x^4 + 4x^3 + 4x^2 + 4x + 3 + 1 = 0
<=> (4x^6 + 4x^5 + x^4) + (2x^4 + 4x^3 + 2x^2) + (2x^2 + 4x + 2) + x^4 + 2 = 0
<=> [2.(2x^3 + x^2)^2 + 2.(√2.x^2 + √2 . x)^2 + 2.(x+1)^2 + x^4] + 2 = 0
Xét tổng các số hạng trong ngoặc vuông, các số hạng đều có thừa số 2>0, thừa số còn lại là bình phương của 1 số sẽ > 0, còn số hạng ngoài ngoặc (số 2) hiển nhiên > 0. Từ đây suy ra phương trình A vô nghiệm.
Còn cách nữa chứng minh phương trình trên vô nghiệm. Nhân cả 2 vế với x-1 rồi thu gọn, ta có phương trình: x^7 - 1 = 0 <=> x = 1.
Ta thấy x = 1 không là nghiệm của phương trình A, vậy ta có phương trình A vô nghiệm.
(Bài tính thì theo bài của bạn, còn phần chứng minh năm ở bài 290, sách Nâng cao và phát triển toán 8 tập 2, trang 15)
P/S: Đình Huy ơi, chỗ (x + 1/x)^3 - 3.x.1/x.(x + 1/x) hình như phải là (x + 1/x)^3 - 3.x.1/x.(x - 1/x) chứ nhỉ?
cách đơn giản hơn nhé.
Đặt \(A=x^6+x^5+x^4+x^3+x^2+x+1=0\)
\(\Leftrightarrow\)\(x^5\left(x+1\right)+x^3\left(x+1\right)+x\left(x+1\right)+1=0\)
\(\Leftrightarrow\)\(\left(x+1\right)\left(x^5+x^3+x\right)+1=0\)
\(\Leftrightarrow\)\(x\left(x+1\right)\left(x^4+x^2+1\right)+1=0\)
Ta có: \(x^4+x^2+1=\left(x^2+\frac{1}{2}\right)+\frac{3}{4}>0\) \(\forall x\)
Nếu \(x\ge0\)thì \(x+1>0\)\(\Rightarrow\)\(x\left(x+1\right)\left(x^4+x^2+1\right)\ge0\)\(\Rightarrow\)\(A>1\)
Nếu \(x=-1\) thì \(x+1=0\)\(\Rightarrow\) \(A=1\)
Nếu \(x< -1\) thì \(x+1< 0\) \(\Rightarrow\) \(A>0\)
Vậy pt vô nghiệm
P/s: sai đâu m.n chỉ cho mk nhé

Phân tích được : \(\left(x^2+\frac{1}{2}\right)^2-\left(y-\frac{1}{2}\right)^2=-10\)
<=> \(\left(x^2-y+1\right)\left(x^2+y\right)=-10\)
Mà \(-10=-1.10=-10.1=-2.5=-5.2\)
Mình làm 1 trường hợp còn lại bạn làm tương tự nha :
VD cặp số đầu tiên là -1.10 => \(\hept{\begin{cases}x^2-y+1=-1\\x^2+y=10\end{cases}}\)
=> \(\hept{\begin{cases}x^2-y=-2\\x^2+y=10\end{cases}}\)=> hoặc x=-2 y=6 hoặc x=2 y=6
Ta có : \(x^4+x^2-y^2+y+10=0\)
\(\Leftrightarrow\left(x^4-y^2\right)+\left(x^2+y\right)=-10\)
\(\Leftrightarrow\left(x^2+y\right)\left(x^2-y\right)+\left(x^2+y\right)=-10\)
\(\Leftrightarrow\left(x^2+y\right)\left(x^2-y+1\right)=-10\)
Vậy nên \(x^2+y;x^2-y+1\inƯ\left(-10\right)=\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
Ta có bảng:
| \(x^2+y\) | -1 | -2 | -5 | -10 | 1 | 2 | 5 | 10 |
| \(x^2-y+1\) | 10 | 5 | 2 | 1 | -10 | -5 | -2 | -1 |
| y | -5 | -3 | -3 | -5 | 6 | 4 | 4 | 6 |
| x | \(\pm2\) | \(\pm1\) | (L) | (L) | (L) | (L) | \(\pm1\) | \(\pm2\) |
| (x;y) | (2;-5) , (-2;-5) | (1;-3) , (-1; -3) | (1;4) , (-1;4) | (2;6) , (-2;6) |
Vậy có 8 cặp số (x;y) thỏa mãn.

Ta có : \(x^2+2012x+2011^{2011}-1=0\)
\(\Leftrightarrow x^2+2012x+1006^2=2011^{2011}+1+1006^2\)
\(\Rightarrow\left(x+1006\right)^2=2011^{2011}+1+1006^2\)
Giả sử x là một số nguyên thì VT là một số chính phương.
Khi đó VP cũng là số chính phương.
Lại có 20112011 có tận cùng là chữ số 1, 10062 có tận cùng là chữ số 6 nên VP có tận cùng là chữ số 8.
Lại có không một số chính phương nào có tận cùng là chữ số 8 hay VP không là số chính phương.
Vậy giả sử sai hay không tồn tại số nguyên x thỏa mãn phương trình trên.
Bạn nên vẽ hình xem:
Vì ta có EK vuông góc AD
BD vuông góc AD
=> EK song song với BD=> \(\frac{AE}{EB}=\frac{AK}{KD}\) (Định lí Ta-Lét)
=> AExKD=AKxEB(dpcm)