Bài 5 : Để làm một chiếc bánh chưng Tết cổ truyền, Vân phải chuẩn bị: gạo nếp, đậu xanh không vỏvà thịt ba chỉ.Trong đó khối lượng đậu xanh bằng 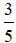 khối lượng gạo nếp, còn lượng nếp bằng 5/2 lượng thit ba chỉ khối lượng thịt ba chỉ. Nếu có 2000 gam gạo nếp thì cần bao nhiêu gam đậu xanh không vỏ và bao nhiêu gam thịt ba chỉ?
khối lượng gạo nếp, còn lượng nếp bằng 5/2 lượng thit ba chỉ khối lượng thịt ba chỉ. Nếu có 2000 gam gạo nếp thì cần bao nhiêu gam đậu xanh không vỏ và bao nhiêu gam thịt ba chỉ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Trên tia Ox, ta có: OM<ON
nên M nằm giữa O và N
=>OM+MN=ON
=>MN+3=8
=>MN=5(cm)
b: M không là trung điểm của MC vì MM=0

a: Đặt \(A=\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}\)
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{100^2}< \dfrac{1}{99\cdot100}=\dfrac{1}{99}-\dfrac{1}{100}\)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
=>\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}< 1-\dfrac{1}{100}< 1\)
=>\(A=1+\dfrac{1}{2^2}+...+\dfrac{1}{100^2}< 1+1=2\)
b: Đặt \(B=\dfrac{1}{3}-\dfrac{1}{3^2}+\dfrac{1}{3^3}-...-\dfrac{1}{3^{100}}\)
=>\(3B=1-\dfrac{1}{3}+\dfrac{1}{3^2}-...-\dfrac{1}{3^{99}}\)
=>\(3B+B=1-\dfrac{1}{3}+\dfrac{1}{3^2}-...-\dfrac{1}{3^{99}}+\dfrac{1}{3}-\dfrac{1}{3^2}+...-\dfrac{1}{3^{100}}\)
=>\(4B=1-\dfrac{1}{3^{100}}\)
=>\(B=\dfrac{1}{4}-\dfrac{1}{4\cdot3^{100}}< \dfrac{1}{4}\)

Ta có: \(3-y=2\left(x-1\right)^2\) (*) và \(2\left(x-1\right)^2\ge0\forall x\)
nên \(3-y\ge0\Rightarrow y\le3\)
\(\Rightarrow y\in\left\{0;1;2;3\right\}\) (vì y là số tự nhiên) (1)
Mặt khác: \(2\left(x-1\right)^2\) là số chẵn với mọi x tự nhiên
\(\Rightarrow3-y\) chẵn \(\Rightarrow y\) lẻ (2)
Từ (1) và (2) \(\Rightarrow y\in\left\{1;3\right\}\)
+, Với \(y=1\) thì (*) thành: \(3-1=2\left(x-1\right)^2\)
\(\Rightarrow2\left(x-1\right)^2=2\)
\(\Rightarrow\left(x-1\right)^2=1\Rightarrow\left[{}\begin{matrix}x-1=1\\x-1=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=0\left(tm\right)\end{matrix}\right.\)
+, Với \(y=3\) thì (*) thành: \(3-3=2\left(x-1\right)^2\)
\(\Rightarrow2\left(x-1\right)^2=0\Rightarrow x-1=0\Rightarrow x=1\left(tm\right)\)
Vậy \(\left(x;y\right)\in\left\{\left(1;3\right);\left(2;1\right);\left(0;1\right)\right\}\) là các cặp giá trị cần tìm.
\(3-y=2\left(x-1^2\right)\)
\(=>\left(3-y\right)-2\left(x-1\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}3-y=0\\2\left(x-1\right)^2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=3\\\left(x-1\right)^2=0\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}y=3\\x-1=0\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}y=3\\x=1\end{matrix}\right.\)
Vậy x = 1; y = 3.

a: Để A là phân số thì \(n+1\ne0\)
=>\(n\ne-1\)
b: Để A là số nguyên thì \(4n+2⋮n+1\)
=>\(4n+4-2⋮n+1\)
=>\(-2⋮n+1\)
=>\(n+1\in\left\{1;-1;2;-2\right\}\)
=>\(n\in\left\{0;-2;1;-3\right\}\)
c: \(A=\dfrac{4n+2}{n+1}=\dfrac{4n+4-2}{n+1}=4-\dfrac{2}{n+1}\)
Để A nhỏ nhất thì \(-\dfrac{2}{n+1}\) nhỏ nhất
=>n+1=1
=>n=0

Bạn cho mình xin bài đọc ạ! (mình nghĩ đọc trong sgk là ra đc chứ bn!)
CON MUỐN LÀM MỘT CÁI CÂY
Ở phố, người ta chỉ trồng được những loại cây be bé. Nhưng sân nhà cũ của Bum lại có một cây ổi. Ông nội kể, lúc mẹ mang bầu nó, ông đã trồng cây ổi này. Ông nghĩ hồi nhỏ ba nó vô cùng thích ổi nên chắc cháu mình cũng sẽ thích ổi như ba nó.
Đúng thật, Bum thích cây ổi lắm. Hồi mới ba, bốn tuổi, nó đã biết cùng ông bắt sâu cho cây ổi nên cây mới lớn như bây giờ. Ông đã bấm để cây có nhiều cành cao, thấp, vững chãi và sai quả. Hương ổi chín toả khắp sân thơm lừng.
Những buổi chiều mát, Bum và bè bạn túm tụm dưới gốc cây, chia nhau những trái ổi chín. Ông nội bắc chiếc ghế đẩu ra sân gần cây ổi, ngồi đó vừa nghe đài vừa nheo nheo mắt nhìn lũ trẻ vui chơi...
Bum đã xa căn nhà cũ và cây ổi ấy ba năm rồi. Vậy mà khi nhớ lại, kỉ niệm như vừa mới đây thôi.
“Con muốn làm một cái cây. Con muốn làm cây ổi trong sân nhà cũ của con, muốn luôn bên đám bạn cùng chia nhau từng trái ổi chín và thấy ông ngồi cười hiền lành bên gốc ổi...”. Bum đã viết như thế trong bài văn nói về ước mơ. Cây ổi trong sân nhà cũ, nó đã nhớ biết bao mà chẳng có dịp nói ra.
Khi cô giáo nói với mẹ về ước mơ của nó, ba mẹ đã ngay lập tức bàn nhau trồng một cây ổi trong sân nhà. Mẹ nói, mai này Bum sẽ mời những người bạn thân ngày xưa đến chơi, cùng trèo hái, chia nhau những trái ổi thơm lừng. Sài Gòn có quá xa Vũng Tàu đâu. Phố cũ và phố mới thực ra sẽ chẳng cách xa khi mà vẫn nhớ về nhau.
Bum nghĩ tới một cây ổi tương lai, vui lâng lâng. Nó bỗng như nghe thấy tiếng chọc ghẹo nhau của lũ bạn và nụ cười hiền hậu của ông nội trôi theo hương ổi chín ngọt lành...
Xem thêm tại: https://loigiaihay.com/bai-7-con-muon-lam-mot-cai-cay-trang-31-sgk-tieng-viet-lop-4-tap-2-ket-noi-tri-thuc-voi-cuoc-song-a137890.html

Một hoạt động thường xuyên được tổ chức nhằm khuyến khích học sinh tập luyện thể dục thể thao đó là hội thi hội khỏe Phù Đổng. Đây là một cuộc thi mang nhiều ý nghĩa nhân văn. Đồng thời giáo dục lòng yêu nước đối với thế hệ trẻ.
Hội khỏe Phù Đổng là đại hội thể dục, thể thao trong nhà trường phổ thông dành cho học sinh Việt Nam do ngành giáo dục Việt Nam tổ chức. Tên gọi của hội thi có ý nghĩa rất lớn. Phù Đổng chính là tên gọi của một trong 31 xã thuộc huyện Gia Lâm thành phố Hà Nội. Phù Đổng nằm trong khu quần tụ của người Việt cổ thuở Vua Hùng dựng nước. Ngày nay tên gọi Phù Đổng gắn liền với truyền thuyết người anh hùng nào Thánh Gióng lừng lẫy, người có công đầu tiên giúp Vua Hùng đánh bại quân xâm lược nhà Ân. Hội khỏe Phù Đổng ra đời với mong muốn là hội thi biểu dương sức khỏe, lấy ý nghĩa từ truyền thuyết đánh giặc ngoại xâm của Thánh Gióng, một người có sức mạnh phi thường, lớn nhanh như thổi, vùng dậy vươn vai đã trở thành tráng sĩ cưỡi ngựa sắt, cầm roi sắt, mặc áo giáp sắt. Các trận đánh giặc dù quân giặc cỏ đông đến đâu cũng không hề khiếp sợ. Và làng Phù Đổng cũng chính là quê hương của Thánh Gióng. Đồng thời hội thi cũng giáo dục về lòng yêu nước, ý thức bảo vệ quốc gia cho thế hệ trẻ. Đồng thời khuyến khích thế hệ thanh thiếu niên rèn luyện sức khỏe.
Trong kỳ thi này có rất nhiều bộ môn thể thao được thi đấu như bóng đá, bóng rổ, bóng chuyền, bơi lội, cầu lông, đá cầu..... Hội khỏe Phù Đổng toàn quốc được tổ chức 4 năm một lần. Cấp khu vực được tổ chức 4 năm một lần, cấp tỉnh tổ chức hai năm một lần, cấp huyện tổ chức hai năm một lần, cấp trường tổ chức mỗi năm một lần. Vì vậy trong 12 năm học học sinh Việt Nam chỉ có thể tham gia tối đa ba Kỳ Hội khỏe Phù Đổng cấp quốc gia và các khu vực 6 kỳ hội khỏe Phù Đổng cấp tỉnh và cấp huyện.
Hội khỏe phù đổng được tổ chức để góp phần duy trì và đẩy mạnh của vận động toàn dân rèn luyện thân thể theo gương Bác Hồ vĩ đại. Thường xuyên tập luyện và thi đấu các môn thể thao cho học sinh phổ thông để nâng cao sức khỏe, phát triển thể chất toàn diện cho học sinh. Hội thi này được tổ chức để phát hiện, bồi dưỡng và đào tạo những tài năng thể dục, thể thao cho đất nước, tổng kết đánh giá công tác giáo dục thể chất và hoạt động thể thao trong các trường học.
Hội khỏe Phù Đổng là một hội thi rất có ý nghĩa đối với thế hệ học sinh. Hội khỏe Phù Đổng ra đời đã giúp nâng cao tinh thần yêu nước, đồng thời khuyến khích việc tập thể dục thể thao cho đối tượng là học sinh trong các nhà trường.
Một hoạt động thường xuyên được tổ chức nhằm khuyến khích học sinh tập luyện thể dục thể thao đó là hội thi hội khỏe Phù Đổng. Đây là một cuộc thi mang nhiều ý nghĩa nhân văn. Đồng thời giáo dục lòng yêu nước đối với thế hệ trẻ.
Hội khỏe Phù Đổng là đại hội thể dục, thể thao trong nhà trường phổ thông dành cho học sinh Việt Nam do ngành giáo dục Việt Nam tổ chức. Tên gọi của hội thi có ý nghĩa rất lớn. Phù Đổng chính là tên gọi của một trong 31 xã thuộc huyện Gia Lâm thành phố Hà Nội. Phù Đổng nằm trong khu quần tụ của người Việt cổ thuở Vua Hùng dựng nước. Ngày nay tên gọi Phù Đổng gắn liền với truyền thuyết người anh hùng nào Thánh Gióng lừng lẫy, người có công đầu tiên giúp Vua Hùng đánh bại quân xâm lược nhà Ân. Hội khỏe Phù Đổng ra đời với mong muốn là hội thi biểu dương sức khỏe, lấy ý nghĩa từ truyền thuyết đánh giặc ngoại xâm của Thánh Gióng, một người có sức mạnh phi thường, lớn nhanh như thổi, vùng dậy vươn vai đã trở thành tráng sĩ cưỡi ngựa sắt, cầm roi sắt, mặc áo giáp sắt. Các trận đánh giặc dù quân giặc cỏ đông đến đâu cũng không hề khiếp sợ. Và làng Phù Đổng cũng chính là quê hương của Thánh Gióng. Đồng thời hội thi cũng giáo dục về lòng yêu nước, ý thức bảo vệ quốc gia cho thế hệ trẻ. Đồng thời khuyến khích thế hệ thanh thiếu niên rèn luyện sức khỏe.
Trong kỳ thi này có rất nhiều bộ môn thể thao được thi đấu như bóng đá, bóng rổ, bóng chuyền, bơi lội, cầu lông, đá cầu..... Hội khỏe Phù Đổng toàn quốc được tổ chức 4 năm một lần. Cấp khu vực được tổ chức 4 năm một lần, cấp tỉnh tổ chức hai năm một lần, cấp huyện tổ chức hai năm một lần, cấp trường tổ chức mỗi năm một lần. Vì vậy trong 12 năm học học sinh Việt Nam chỉ có thể tham gia tối đa ba Kỳ Hội khỏe Phù Đổng cấp quốc gia và các khu vực 6 kỳ hội khỏe Phù Đổng cấp tỉnh và cấp huyện.
Hội khỏe phù đổng được tổ chức để góp phần duy trì và đẩy mạnh của vận động toàn dân rèn luyện thân thể theo gương Bác Hồ vĩ đại. Thường xuyên tập luyện và thi đấu các môn thể thao cho học sinh phổ thông để nâng cao sức khỏe, phát triển thể chất toàn diện cho học sinh. Hội thi này được tổ chức để phát hiện, bồi dưỡng và đào tạo những tài năng thể dục, thể thao cho đất nước, tổng kết đánh giá công tác giáo dục thể chất và hoạt động thể thao trong các trường học.
Hội khỏe Phù Đổng là một hội thi rất có ý nghĩa đối với thế hệ học sinh. Hội khỏe Phù Đổng ra đời đã giúp nâng cao tinh thần yêu nước, đồng thời khuyến khích việc tập thể dục thể thao cho đối tượng là học sinh trong các nhà trường.

