b) xét ΔANK và ΔBNC, có:

NK = NC (gt)

\(\widehat{ANK}=\widehat{BNC}\) (đối đỉnh)

NB = NA (gt)

⇒ ΔANK = ΔBNC (c-g-c)

vì M là trung điểm của BC nên ta có: \(BC=MB+MC=2MC\)

mà KA = BC (2 cạnh tương ứng)

\(\Rightarrow BC=KA=2MC\)

c) ta có MB = MC (giả thiết) 

⇒ MA là đường trung tuyến của ΔABC

⇒ MA cũng là đường phân giác của ΔABC

⇒ MA là đường phân giác của \(\widehat{BAC}\)

\(\widehat{BAC}=\widehat{BAM}+\widehat{MAC}=2\widehat{BAM}\\ \Rightarrow\widehat{BAM}=\dfrac{\widehat{BAC}}{2}=\dfrac{50^0}{2}=25^0\left(1\right)\)

Vì ΔABC cân tại A nên

\(\widehat{B}=\widehat{C}=\dfrac{\left(180^0-\widehat{A}\right)}{2}=\dfrac{\left(180^0-50^0\right)}{2}=\dfrac{130^0}{2}=65^0\)

mà \(\widehat{KAB}=\widehat{ABC}\) (2 góc tương ứng)

\(\Rightarrow\widehat{KAB}=65^0\left(2\right)\)

Từ (1) và (2) ta có:

\(\widehat{KAM}=\widehat{KAB}+\widehat{AMB}=65^0+25^0=90^0\)

có ai làm câu d chưa cho mình xin hướng dẫn ạ

Câu 4:

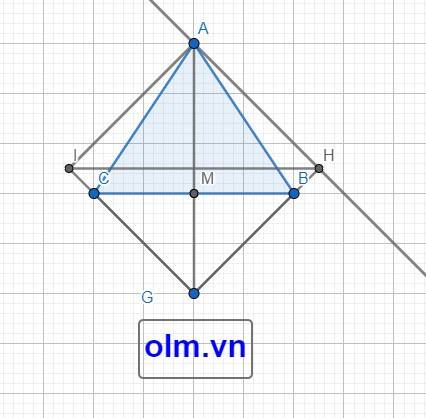
Vì tam giác ABC cân tại A; AM là đường cao của tam giác ABC

Nên AM là trung trực của BC (trong tam giác cân đường cao cũng là đường trung trực của tam giác)

⇒ GC = GB ⇒ tam giác BCG cân tại G

  ⇒ GM là phân giác của góc CGB (vì trong tam giác cân đường cao cũng là đường phân giác)

⇒ \(\widehat{CGM}\) = \(\dfrac{1}{2}\) \(\widehat{BGC}\) = 90⁰ x \(\dfrac{1}{2}\) = 45⁰

Xét tam giác vuông AIG có: 

\(\widehat{IAG}\) = 90⁰ - \(\widehat{IGA}\) = 90⁰ - 45⁰ = 45⁰

⇒ \(\widehat{IGA}\) = \(\widehat{IAG}\) = 45⁰

⇒ tam giác AIG vuông cân tại I

⇒ IA = IG

AH // GI ⇒ AH \(\perp\) AI (vì một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại)

 \(\widehat{IAH}\) = 90⁰

Xét tứ giác: AHGI có:

\(\widehat{IAH}\) = \(\widehat{AIG}\) = \(\widehat{IGH}\) = 90⁰; IA = IG (cmt)

⇒ AHGI là hình vuông

⇒ AG \(\perp\) HI  (tính chất hai đường chéo của hình vuông)

Mặt khác  AG \(\perp\) BC (gt)

⇒ HI // BC (vì hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)

Kết Luận: HI // BC (đpcm)

Khi x=-3 thì \(\left(x^{2023}+3x^{2022}+1\right)^{2000}=\left[\left(-3\right)^{2023}+3\cdot\left(-3\right)^{2022}+1\right]^{2000}\)

\(=\left[-3^{2023}+3^{2023}+1\right]^{2000}\)

\(=1^{2000}=1\)

Đề thiếu. Bạn xem lại đề.

\(2x=\dfrac{y}{3}=\dfrac{z}{5}\)

=>\(\dfrac{x}{0,5}=\dfrac{y}{3}=\dfrac{z}{5}\)

mà \(\dfrac{x+y-z}{2}=-20\)

nên \(\dfrac{x}{0,5}=\dfrac{y}{3}=\dfrac{z}{5}=\dfrac{x+y-z}{0,5+3-5}=\dfrac{-40}{-1,5}=\dfrac{40}{1,5}\)

=>\(x=\dfrac{20}{1,5}=\dfrac{40}{3};y=\dfrac{40}{1,5}\cdot3=80;z=40\cdot\dfrac{5}{1,5}=40\cdot\dfrac{10}{3}=\dfrac{400}{3}\)

Ta có: \(\widehat{ABE}=\dfrac{\widehat{ABC}}{2}\)

\(\widehat{ACF}=\dfrac{\widehat{ACB}}{2}\)

mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)

nên \(\widehat{ABE}=\widehat{ACF}\)

Xét ΔABE và ΔACF có

\(\widehat{ABE}=\widehat{ACF}\)

AB=AC

\(\widehat{BAE}\) chung

Do đó: ΔABE=ΔACF

=>BE=CF

a: Xét ΔABI và ΔACI có

AB=AC

BI=CI

AI chung

Do đó: ΔABI=ΔACI

b: Sửa đề: Chứng minh AC=AE

Ta có: CE//AI

=>\(\widehat{AEC}=\widehat{BAI};\widehat{CAI}=\widehat{ACE}\)

mà \(\widehat{BAI}=\widehat{CAI}\)(ΔABI=ΔACI)

nên \(\widehat{AEC}=\widehat{ACE}\)

=>AC=AE

Gọi a (tờ), b (tờ), c (tờ) lần lượt là số tờ tiền polime ứng với loại 20000 đồng, 50000 đồng và 100000 đồng (a, b, c ∈ ℕ*)

Do tổng số tờ tiền là 24 tờ nên ta có:

a + b + c = 24

Do trị giá của mỗi loại tiền là như nhau nên:

20000a = 50000b = 100000c

2a = 5b = 10c

⇒ a/(1/2) = b/(1/5) = c/(1/10)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

a/(1/2) = b/(1/5) = c/(1/10) = (a + b + c)/(1/2 + 1/5 + 1/10) = 24/(4/5) = 30

2a = 30 ⇒ a = 30 : 2 = 15 (nhận)

5b = 30 ⇒ b = 30 : 5 = 6 (nhận)

10c = 30 ⇒ c = 30 : 10 = 3 (nhận)

Vậy số tờ tiền ứng với loại 20000 đồng; 50000 đồng; 10000 đồng lần lượt là: 15 tờ, 6 tờ; 3 tờ