Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$3A=1.2(3-0)+2.3(4-1)+3.4(5-2)+....+2020.2021(2022-2019)$
$=(1.2.3+2.3.4+3.4.5+....+2020.2021.2022)-(0.1.2+1.2.3+2.3.4+....+2019.2020.2021)$
$=2020.2021.2022$
$\Rightarrow A=\frac{2020.2021.2022}{3}$

Bạn nên tách lẻ từng bài từng post ra để khả năng nhận được sự trợ giúp cao hơn nhé. Đăng quá nhiều bài trong 1 post (nhất là bài hình) khiến mọi người nản, dễ bỏ qua bài của bạn hơn.

Gọi các phân số cần tìm là: \(\dfrac{a}{b}\) theo bài ra ta có:
\(\dfrac{a}{b}\) = \(\dfrac{a+2}{b\times2}\)
a.(b x 2) = (a + 2) x b
ab x 2 = ab + 2b
ab = 2b
a = 2
Ta có: \(\dfrac{2}{b}\) > \(\dfrac{1}{5}\) = \(\dfrac{2}{10}\)
⇒ b < 10 ⇒ b = 1; 2; 3; 4; 5; 6; 7; 8; 9
Vì \(\dfrac{2}{b}\) không phải là số tự nhiên nên b \(\in\) {3; 4; 5; 6; 7; 8; 9}
Bài 16:
\(\dfrac{1}{6}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + \(\dfrac{1}{7^2}\) +...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\)
\(\dfrac{1}{5^2}\) < \(\dfrac{1}{4.5}\) = \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\)
\(\dfrac{1}{6^2}\) < \(\dfrac{1}{5.6}\) = \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\)
............................
\(\dfrac{1}{100^2}\) < \(\dfrac{1}{99.100}\) = \(\dfrac{1}{99}\) - \(\dfrac{1}{100}\)
Cộng vế với vế ta có:
\(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\)+...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) - \(\dfrac{1}{100}\) < \(\dfrac{1}{4}\) (1)
\(\dfrac{1}{5^2}\) > \(\dfrac{1}{5.6}\) = \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\)
\(\dfrac{1}{6^2}\) > \(\dfrac{1}{6.7}\) = \(\dfrac{1}{6}\) - \(\dfrac{1}{7}\)
...............................
\(\dfrac{1}{100^2}\) > \(\dfrac{1}{100.101}\) = \(\dfrac{1}{100}\) - \(\dfrac{1}{101}\)
Cộng vế với vế ta có:
\(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + ... + \(\dfrac{1}{100^2}\) > \(\dfrac{1}{5}\) - \(\dfrac{1}{101}\)= \(\dfrac{96}{505}\) > \(\dfrac{96}{576}\) = \(\dfrac{1}{6}\) (2)
Kết hợp (1) và (2) ta có:
\(\dfrac{1}{6}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) +...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) (đpcm)

\(A=\dfrac{1}{2^4}+\dfrac{1}{2^5}+\dfrac{1}{2^6}+\dots+\dfrac{1}{2^{100}}\)
\(2A=\dfrac{1}{2^3}+\dfrac{1}{2^4}+\dfrac{1}{2^5}+\dots+\dfrac{1}{2^{99}}\)
\(2A-A=\left(\dfrac{1}{2^3}+\dfrac{1}{2^4}+\dfrac{1}{2^5}+\dots+\dfrac{1}{2^{99}}\right)-\left(\dfrac{1}{2^4}+\dfrac{1}{2^5}+\dfrac{1}{2^6}+\dots+\dfrac{1}{2^{100}}\right)\)
\(A=\dfrac{1}{2^3}-\dfrac{1}{2^{100}}\)
\(A=\dfrac{2^{97}}{2^{100}}-\dfrac{1}{2^{100}}\)
\(A=\dfrac{2^{97}-1}{2^{100}}\)


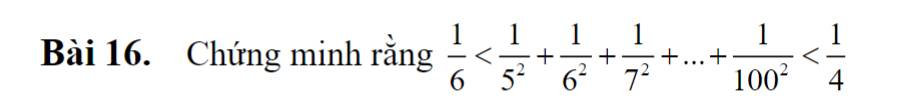 Cứu mình gấp ạ!!! Mình sắp thi rồi!!!
Cứu mình gấp ạ!!! Mình sắp thi rồi!!!