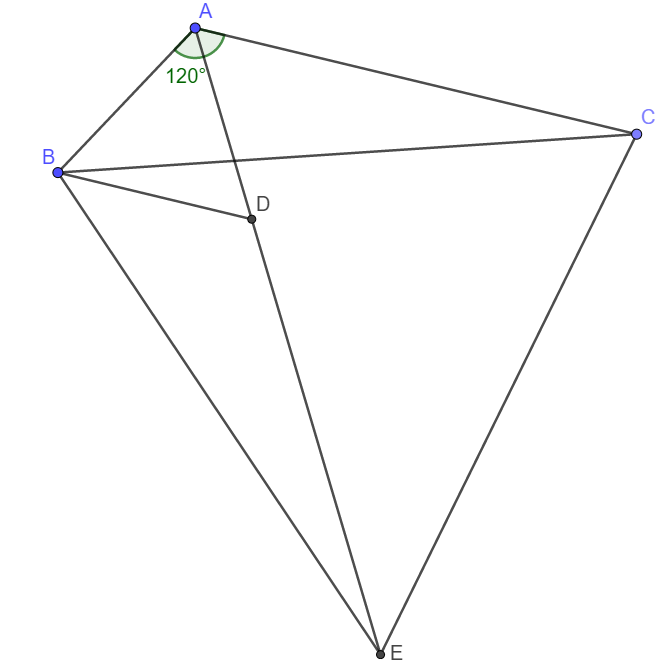
Cho tam giác ABC vuông tại A, có AC = 5 cm, BC = 13 cm
a)TÍnh độ dài cạnh AB
b)Trên tia AC lấy điểm D sao cho AB=AD. Vẽ AE vuông góc với BD (E thuộc BD). C/m tam giác AED=tam giác AEB và AE là tia phân giác góc BAD
c)AE cắt BC tại F.C/m góc ADF=góc ABF
d)Đường thẳng vuông góc với BC tại F cắt tia CA tại H. C/m FB=FH
AI LÀM ĐÚNG VÀ NHANH MÌNH TICK CHO :DD