Dễ dàng chứng minh được HCDB là hình bình hành ( 2 cặp cạnh đối song song )
=> HA + HD = HO + OA + HO + OD = 2HO + ( OA + OD ) = 2HO (1)
Có : OA = OH + HA
OB = OH + HB
OC = OH + HC 
=> OA + OB + OC = 3.OH + HA + HB + HC = 3. OH + HA + HD (2)
(1) (2) => OA + OB +OC = 3.OH + 2HO = OH (3)
G là trọng tâm tam giác ABC => OA + OB + OC = 3.OG (4)
(3) (4) => OH = 3.OG => OH, OG cùng phương => O, G, H thẳng hàng ( đpcm )

:A

Mình làm theo cách này hơi dài. Mình có đặt thêm điểm và tạo nhiều hình để làm. Có gì sai sót thông cảm nhé

Cho tam giác ABC nhọn có M,N lần lượt là trung điểm BC và AC. Đường thằng vuông góc với AB kẻ từ B và đường thăng vuông góc với AC kẻ từ C cắt nhau tại D. Gọi H là trực tâm, G là trọng tâm, O là tâm đường tròn ngoại tiếp tam giác ABC

                                                          Giải:

Bạn là CTV nên mình chỉ ghi ý chính thôi

Chứng minh H,M,D thẳng hàng và MH=MD

Do G là trọng tâm tam giác ABC nên 

\(\frac{AG}{AM}=\frac{2}{3}\)

M là trung điểm HD

Nên G cũng là trọng tâm tam giác AHD  (*)

Xét tam giác ACD có  NA=ND

                                    NO//CD

=> O là trung điểm AD

=> HO là trung tuyếntam giác AHD(**)

Từ (*) và (**) => H,G,O thẳng hàng

Làm kinh tinh cái gì z

Chim cánh cụt có thể bơi lặn trong nước với vận tốc từ 6 tới 12 km/h, mặc dù có một số báo cáo cho rằng tốc độ có thể lên tới 27 km/h (điều này có thể xảy ra khi chúng bị giật mình hay bị tấn công). Các loài chim cánh cụt nhỏ không lặn sâu và chỉ săn tìm mồi gần mặt nước và chỉ lặn khoảng 1-2 phút. Các loài chim cánh cụt lớn có thể lặn sâu khi cần thiết. Kỷ lục lặn sâu của chim cánh cụt hoàng đế lớn đã được ghi nhận là tới độ sâu 565 m (1.870 ft) và kéo dài tới 20 phút.

Chim cánh cụt có thể đi lạch bạch bằng hai chân hoặc trượt bằng bụng của chúng dọc theo lớp tuyết, một chuyển động gọi là "trượt băng", điều này cho phép chúng tiết kiệm năng lượng trong khi vẫn có thể chuyển động tương đối nhanh.

Phần lớn chim cánh cụt ăn các loại nhuyễn thể, cá, mực và các dạng sinh vật biển khác chúng bắt được trong khi bơi lội dưới nước. Chúng tiêu tốn khoảng một nửa thời gian trên cạn và nửa còn lại dưới lòng các đại dương.

Một số loài chim cánh cụt có thể giao phối cả đời, trong khi các loài khác chỉ giao phối một mùa. Nói chung, chúng tạo ra một bầy con nhỏ và cả chim bố lẫn chim mẹ cùng chăm sóc con non.

Ở một số loài con cái đẻ ít trứng (1-2 trứng), ấp 65 ngày. Sau mỗi lần ấp, con cái giảm 40-50% khối lượng. Sau khi trứng nở, con mẹ tiếp tục ủ ấm cho con non.

đề bài là j vậy bn ơi

đề:  thu gọn đa thức

\(3x^2+7x^3-3x^3+6x^3-3x^2\)

\(=\left(3x^2-3x^2\right)+\left(7x^3-3x^3+6x^3\right)\)

\(=10x^3\)

\(3x^2+7x^3-3x^3+6x^3-3x^2\)

\(=3x^2+7x^3-3x^3+6x^3-3x^3=10x^3\)có bậc 3

\(\frac{4^2.5.11}{44.20}=\frac{2^4.5.11}{2^2.11.2^2.5}=\frac{2^4.5.11}{2^4.5.11}=1\)

\(\frac{13.15.6}{18.65.7}=\frac{13.3.5.2.3}{2.3^2.13.5.7}=\frac{3^2.2.5.13}{2.3^2.13.5.7}=\frac{1}{7}\)

B B A A C C M M N N J J

a) Ta thấy \(\widehat{MAC}=\widehat{MAB}+\widehat{BAC}=90^o+\widehat{BAC}=\widehat{CAN}+\widehat{BAC}=\widehat{BAN}\)

Xét tam giác MAC và BAN có:

MA = BA

AC = AN

\(\widehat{MAC}=\widehat{BAN}\)

\(\Rightarrow\Delta MAC=\Delta BAN\left(c-g-c\right)\Rightarrow MC=BN\)

b) Gọi giao điểm của MC và BN là J.

Ta có: \(\widehat{JBA}=\widehat{JMA}\)(Vì \(\Delta MAC=\Delta BAN\left(c-g-c\right)\) )

Vậy nên \(\widehat{MBJ}+\widehat{BMJ}=\widehat{MBA}+\widehat{JBA}+\widehat{BMJ}=\widehat{MBA}+\widehat{JMA}+\widehat{BMJ}\)

\(=\widehat{MBA}+\widehat{BMA}=90^o\)

Xét tam giác MBJ có \(\widehat{MBJ}+\widehat{BMJ}=90^o\Rightarrow\widehat{BJM}=90^o\Rightarrow BN\perp MC\)

c) Giả sử tam giác ABC đều cạnh 4 cm thì AB = AC = MA = NA = 4cm

Khi đó áp dụng định lý Pi-ta-go cho tam giác vuông cân MAB và NAC thì \(MB=NC=4\sqrt{2}\left(cm\right)\)

d) Khi tam giác ABC đều cạnh 4cm thì AMC và NAB là các tam giác cân có góc ở đỉnh là: 90^o + 60^o = 150^o

Suy ra \(\widehat{AMC}=\widehat{ACM}=\frac{180^o-150^o}{2}=15^o\)

Vậy thì \(\widehat{MCB}=\widehat{ACB}-\widehat{ACM}=60^o-15^o=45^o\)

Ta có \(\widehat{MAN}=360^o-90^o-60^o-90^o=120^o\)

Tam giác MAN cũng cân tại A nên \(\widehat{AMN}=\frac{180^o-120^o}{2}=30^o\)

\(\Rightarrow\widehat{CMN}=30^o+15^o=45^o\)

Suy ra \(\widehat{CMN}=\widehat{MCB}\)

Chúng lại ở vị trí so le trong nên BC // MN.

Em cảm ơn cô

Ta có :

\(7.3^{x-1}-3^{x+2}=-540\)

\(\Leftrightarrow\)\(7.3^x:3-3^x.3^2=-540\)

\(\Leftrightarrow\)\(\frac{7}{3}.3^x-9.3^x=-540\)

\(\Leftrightarrow\)\(3^x\left(\frac{7}{3}-9\right)=-540\)

\(\Leftrightarrow\)\(3^x.\frac{-20}{3}=-540\)

\(\Leftrightarrow\)\(3^x=\left(-540\right):\frac{-20}{3}\)

\(\Leftrightarrow\)\(3^x=81\)

\(\Leftrightarrow\)\(3^x=3^4\)

\(\Leftrightarrow\)\(x=4\)

Vậy \(x=4\)

lên sách giải lớp 7 mà nhìn bạn đỡ phải tốn thời gian

A B C K K' H

Ta có: \(AC-AB>CK-BH\)    (*)

\(\Leftrightarrow AC+BH>AB+CK\)

\(\Leftrightarrow\left(AC+BH\right)^2>\left(AB+CK\right)^2\)

\(\Leftrightarrow AC^2+BH^2+2.AC.BH>AB^2+CK^2+2.AB.CK\)

\(\Leftrightarrow AC^2+BH^2+4S_{ABC}>AB^2+CK^2+4S_{ABC}\)

\(\Leftrightarrow AC^2+BH^2>AB^2+CK^2\)

\(\Leftrightarrow AK>AH\)  (**)

Xét tam giác ABC có \(\widehat{B}>\widehat{C}\Rightarrow AC>AB\)

Trên AC lấy điểm B' sao cho AB' = AB \(\Rightarrow AB'< AC\Rightarrow\) B' nằm giữa A và C.  (1)

Kẻ B'K' vuông góc AB tại K'.Suy ra B'K' // KC   (2)

Từ (1) và (2) suy ra K' nằm giữa A và K hay AK' < AK

Ta thấy ngay \(\Delta ABH=\Delta ACK'\)  (Cạnh huyền - góc nhọn) 

\(\Rightarrow AH=AK'\Rightarrow AK>AH\)

Vậy (**) đúng hay (*) đúng.

A B C K H

Ta có tam giác AKC vuông tại K

=> AC là cạnh lớn nhất (nhận xét quan hệ giữa cạnh đối diện với góc lớn hơn)

=>AC > CK

Ta có tam giác ABH vuông tại H

=> AB là cạnh lớn nhất (nhận xét quan hệ giữa cạnh đối diện với góc lớn hơn)

=> AB > BH

 Có: AC>CK;

AB>BH (cmt)

=> AC-AB > CK-BH

làm j có tam giác nào cân tại A ( A<90^o)

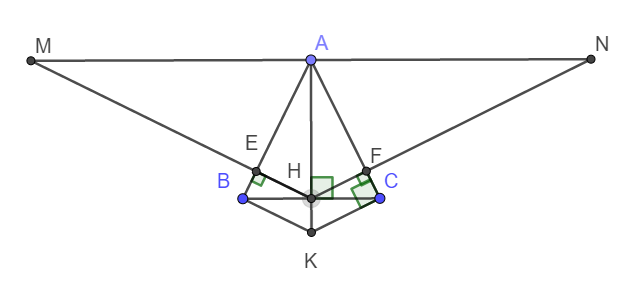
a) Xét tam giác vuông ABH và tam giác vuông ACH có:

Cạnh AH chung

AB = AC (gt)

\(\Rightarrow\widehat{BAH}=\widehat{CAH}\)  (Hai góc tương ứng)

Vậy nên AH là tia phân giác góc BAC.

b) Xét hai tam giác vuông AEH và AFH có:

Cạnh AH chung

\(\widehat{EAH}=\widehat{FAH}\)

\(\Rightarrow\Delta AEH=\Delta AFH\)  (Cạnh huyền - góc nhọn)

\(\Rightarrow HE=HF\)  (Hai cạnh tương ứng)

Suy ra tam giác HEF cân tại E.

c) Dễ thấy \(\Delta ABK=\Delta ACK\left(c-g-c\right)\)

\(\Rightarrow\widehat{AKB}=\widehat{AKC}\)

Lại có \(\widehat{AKC}=\widehat{AHF}\)   (Đồng vị) 

\(\widehat{AHF}=\widehat{AHE}\) (Do \(\Delta AEH=\Delta AFH\) )

\(\Rightarrow\widehat{AKB}=\widehat{AHE}\) hay HE // BK

d) Ta có \(\Delta AHN=\Delta AHM\left(c-g-c\right)\)

\(\Rightarrow\widehat{MAH}=\widehat{NAH}=90^o\)

\(\Rightarrow\widehat{MAN}=180^o\) hay M, N, A thẳng hàng.

\(a^2+b^2+c^2=a^3+b^3=c^3=1\)

\(\Rightarrow\)\(a;b;c\in\left\{-1;1\right\}\)

\(\Rightarrow\)\(a^3+b^3+c^3-\left(a^2+b^2+c^2\right)=a^2\left(a-1\right)+b^2\left(b-1\right)+c^2\left(c-1\right)\le0\)

\(\Rightarrow\)\(a^3+b^3+c^3\le1\Rightarrow a;b;c\)nhận 2 giá trị là 0 hoặc 1

\(\Rightarrow\)\(b^{2012}=b^2;c^{2013}=c^2\)

\(\Rightarrow\)\(S=a^2+b^{2012}+c^{2013}=1\)

Vậy tự kết luận lấy

Câu hỏi của Nguyễn Nhật Quỳnh Trang 11/03/2016 vào lúc 18:52