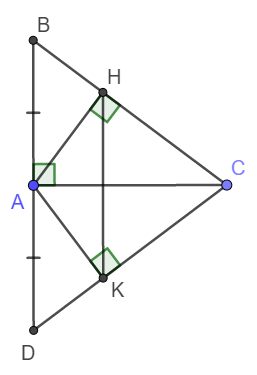
Cho tam giác ABC vuông tại A.Trên cạnh BC lấy điểm E sao cho BE=BA.Qua E kẻ đường thẳng d vuông góc với BC và d cắt AC tại D
a)Chứng minh tam giác ABD=tam giác EBD
b)Gọi H là giao điểm của đường thẳng Ab và đường thẳng B.Chứng minh tam giác ADH=tam giác EDC
c)Chứng minh tam giác HBC cân
giải giúp mình nha!
Giải đúg mình tick cho
Vẽ hình hay ko vẽ hình cũg được

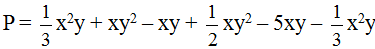
a) Xét tam giác vuông ABD và tam giác vuông EBD có:
Cạnh BD chung
BA = BE (gt)
\(\Rightarrow\Delta ABD=\Delta EBD\) (Cạnh huyền - cạnh góc vuông)
b) Do \(\Delta ABD=\Delta EBD\Rightarrow AD=ED\)
Xét tam giác vuông ADH và tam giác vuông EDC có:
AD = ED
\(\widehat{ADH}=\widehat{EDH}\)
\(\Rightarrow\Delta ADH=\Delta EDH\) (Cạnh góc vuông, góc nhọn kề)
c) Do \(\Delta ADH=\Delta EDH\Rightarrow AH=EH\)
Lại có BA = BE nên BH = BA AH = AE + EC = BC
Xét tam giác HBC có BH = BC nên HBC là tam giác cân.
cho em hỏi đường thẳng d thường đâu rồi chị?