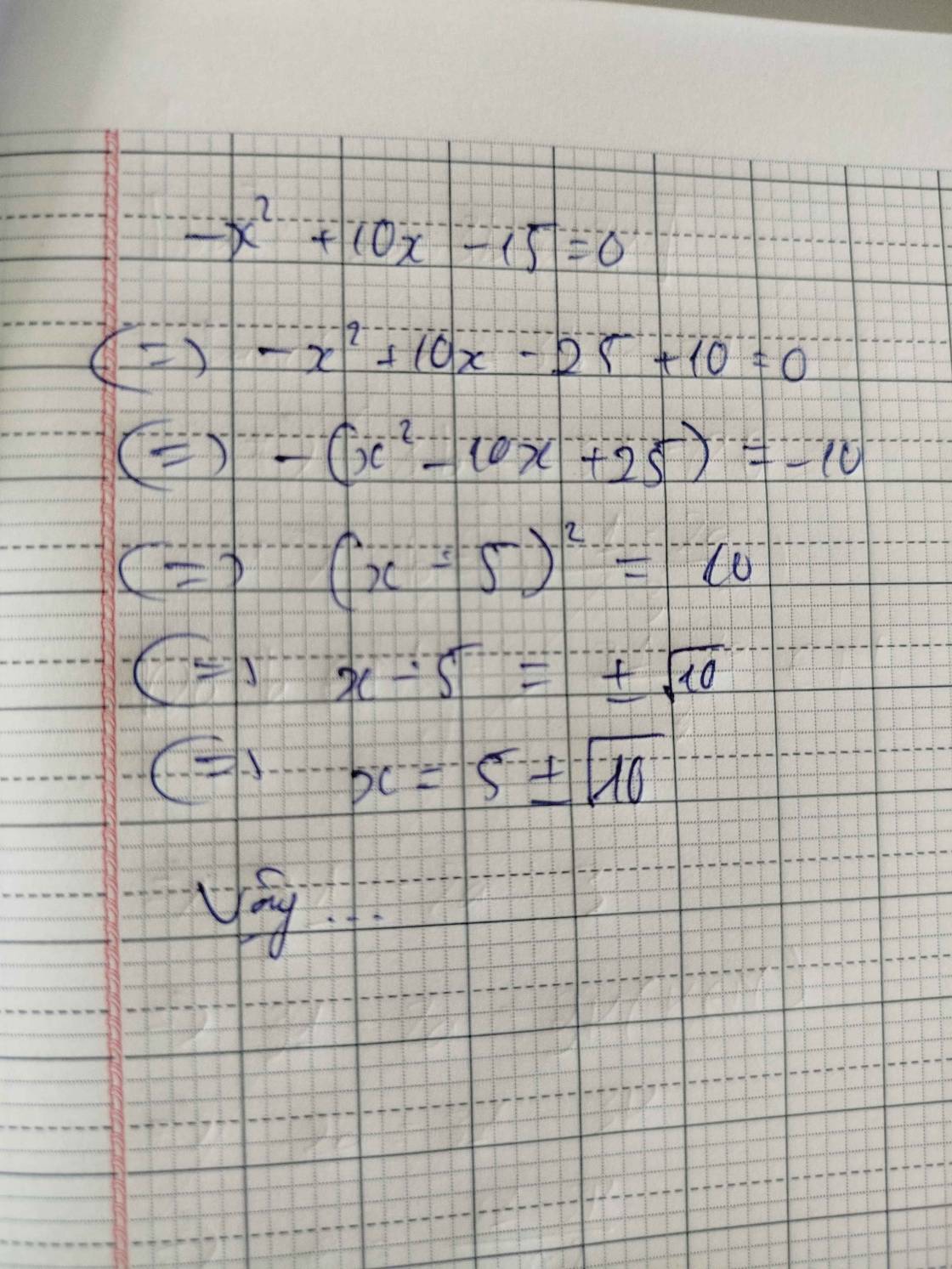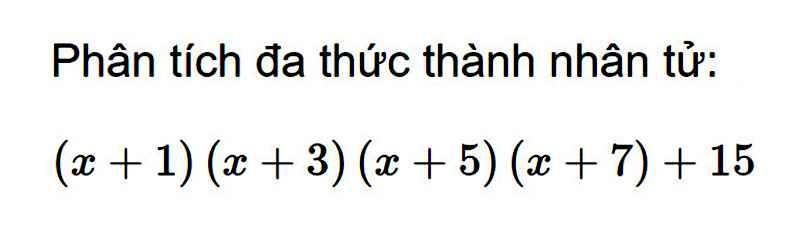\(\frac{1}{\left(x^{2}+3x+2\right)}+\frac{1}{\left(x^{2}+5x+6\right)}+\frac{1}{\left(x^{2}+7x+12\right)}=\frac{3}{x^{2}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
Xét ΔBAC có BE là phân giác
nên \(\dfrac{AE}{AB}=\dfrac{CE}{CB}\)
=>\(\dfrac{AE}{6}=\dfrac{CE}{10}\)
=>\(\dfrac{AE}{3}=\dfrac{CE}{5}\)
mà AE+CE=AC=8cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AE}{3}=\dfrac{CE}{5}=\dfrac{AE+CE}{3+5}=\dfrac{8}{8}=1\)
=>\(AE=3\cdot1=3\left(cm\right)\)
b: Xét ΔBAE vuông tại A và ΔBCM vuông tại C có
\(\widehat{ABE}=\widehat{CBM}\)
Do đó: ΔBAE~ΔBCM
=>\(\widehat{BEA}=\widehat{BMC}\)
=>\(\widehat{CME}=\widehat{CEM}\)
=>ΔCEM cân tại C


x=2024 nên x-1=2023
\(H=x^{14}-2023x^{13}-2023x^{12}-...-2023x-2023\)
\(=x^{14}-x^{13}\left(x-1\right)-x^{12}\left(x-1\right)-...-x\left(x-1\right)-\left(x-1\right)\)
\(=x^{14}-x^{14}+x^{13}-x^{13}+x^{12}-...-x^2+x-x+1\)
=1

`(x+1)(x+3)(x+5)(x+7)+15`
`=(x+1)(x+7)(x+3)(x+5)+15`
`= (x^2+7x+x+7)(x^2+5x+3x+15)+15 `
`=(x^2 +8x+7)(x^2+8x+15)+15`
Đặt `t=x^2 +8x+11`
`=(t-4)(t+4)+15`
`=t^2 -16 +15`
`=t^2 -1`
`=(t-1)(t+1)`
`=(x^2 +8x+11-1)(x^2 +8x+11+1)`
`=(x^2 +8x+10)(x^2 +8x+12)`

2x³ - 5x² + 8x - 3
= 2x³ - x² - 4x² + 2x + 6x - 3
= (2x³ - x²) - (4x² - 2x) + (6x - 3)
= x²(2x - 1) - 2x(2x - 1) + 3(2x - 1)
= (2x - 1)(x² - 2x + 3)

a: ĐKXĐ: \(x\notin\left\{0;2\right\}\)
b: \(C=\dfrac{x^2}{x-2}\cdot\left(\dfrac{x^2+4}{x}-4\right)+3\)
\(=\dfrac{x^2}{x-2}\cdot\dfrac{x^2-4x+4}{x}+3\)
\(=\dfrac{x^2\left(x-2\right)^2}{x\left(x-2\right)}+3=x\left(x-2\right)+3=x^2-2x+3\)

a)
\(\dfrac{x^4+12x^2-5x}{-x}=-\dfrac{x^4}{x}-\dfrac{12x^2}{x}+\dfrac{-5x}{-x}=-x^3-12x+5\)
b)
\(\dfrac{15x^5y^9-10x^3y^5+25x^4y^4}{5x^2y^2}=\dfrac{15x^5y^9}{5x^2y^2}-\dfrac{10x^3y^5}{5x^2y^2}+\dfrac{25x^4y^4}{5x^2y^2}=3x^3y^7-2xy^3+5x^2y^2\)
`a)`
`(x^4 + 12x^2 -5x):(-x)`
`=[x^4 : (-x)] + [12x^2 : (-x)] - [5x:(-x)]`
`=-x^3 - 12x + 5`
`b)`
`(15 x^5 y^9 - 10 x^3 y^5 + 25 x^4 y^4) : 5x^2 y^2`
`=(15 x^5 y^9 : 5 x^2 y^2) - (10 x^3 y^5 : 5x^2 y^2) + (25 x^4 y^4 : 5 x^2 y^2)`
`=3 x^3 y^7 - 2 x y^3 + 5 x^2 y^2`

a + b = m
a - b = n
=> a = (m + n)/2
b = (m - n)/2
Có: a.b = (m + n)/2.(m - n)/2
= (m^2 - n^2)/4
=> a^3 - b^3 = (m + n)^3/2^3 - (m - n)^2/2^3
= (m + n)^3/8 - (m - n)^3/8
= [(m + n)^3 - (m - n)^3]/8
= [(m + n - m + n)((m + n)^2 + (m + n)(m - n) + (m - n)^2)]/8
= [n(m^2 + n^2 + 2mn + m^2 - n^2 + m^2 + n^2 - 2mn)]/8
= n(3m^2 + 2n^2)/8
= m^2n − (m^2−n^2)/4 .n

Gọi H,K lần lượt là trung điểm của AD,BC
Xét hình thang ABCD có
H,K lần lượt là trung điểm của AD,BC
=>HK là đường trung bình của hình thang ABCD
=>HK//AB//CD và \(HK=\dfrac{AB+CD}{2}=17\left(cm\right)\)
Xét ΔDAB có
H,M lần lượt là trung điểm của DA,DB
=>HM là đường trung bình của ΔDAB
=>HM//AB và \(HM=\dfrac{AB}{2}=\dfrac{15}{2}=7,5\left(cm\right)\)
Xét ΔCAB có
N,K lần lượt là trung điểm của CA,CB
=>NK là đường trung bình của ΔCAB
=>NK//AB và \(NK=\dfrac{AB}{2}=7,5\left(cm\right)\)
Ta có: NK//AB
HK//AB
mà HK,NK có điểm chung là K
nên H,N,K thẳng hàng
Ta có: HM//AB
HK//AB
=>H,M,K thẳng hàng
=>H,M,N,K thẳng hàng
Ta có: HM+MN+NK=HK
=>MN+7,5+7,5=17
=>MN=2(cm)