(\(x+y\)) = a; (\(x^3\) + y³) = b. 

 \(x^3\) + y³ = (\(x\) + y).(\(x^2\) - \(xy\) + y²) (1)

Thay \(x\) + y = a; \(x^3\) + y³ = b vào biểu thức (1) ta có:

 a.(\(x^2\) - \(xy\) + y²) =  b

     \(x^2\) - \(xy\) + y² = \(\dfrac{b}{a}\)

     \(x^2\) + 2\(xy\) + y² - 3\(xy\) = \(\dfrac{b}{a}\)

    (\(x+y\))² - 3\(xy\)           = \(\dfrac{b}{a}\)

         a² - 3\(xy\)               = \(\dfrac{b}{a}\)

               3\(xy\)                = a² - \(\dfrac{b}{a}\)

                \(xy\)                 = (\(a^2\) - \(\dfrac{b}{a}\)): 3

                \(xy\)               = \(\dfrac{a^3-b}{3a}\)

    Thay \(xy\) = \(\dfrac{a^3-b}{3a}\) vào biểu thức:

               \(x^2\) - \(xy\) + y² = \(\dfrac{b}{a}\) ta có 

                \(x^2\)  - \(\dfrac{a^3-b}{3a}\)+ y²  = \(\dfrac{b}{a}\)

                  \(x^2\) + y² = \(\dfrac{b}{a}\) + \(\dfrac{a^3-b}{3a}\)

                 \(x^2\)  + y² = \(\dfrac{3b+a^3-b}{3a}\)

                 \(x^2\) + y² = \(\dfrac{a^3+2b}{3a}\)

Bài 6: Ta có:

\(4x^2+2y^2+2z^2-4xy-4xz+2yz-6y-10z+34=0\)

\(\Leftrightarrow4x^2+y^2+z^2-4xy-4xz+2yz+y^2-6y+9+z^2-10z+25=0\)

\(\Leftrightarrow\left[\left(2x\right)^2+y^2+z^2-2\cdot2x\cdot y-2\cdot2x\cdot z+2\cdot y\cdot z\right]+\left(y^2-6y+9\right)+\left(z^2-10z+25\right)=0\)

\(\Leftrightarrow\left(2x-y-z\right)^2+\left(y-3\right)^2+\left(z-5\right)^2=0\)

Mà: \(\left(2x-y-z\right)^2+\left(y-3\right)^2+\left(z-5\right)^2\ge0\forall x,y,z\)

Mặt khác: \(\left(2x-y-z\right)^2+\left(y-3\right)^2+\left(z-5\right)^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x-y-z=0\\y-3=0\\z-5=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x-3-5=0\\y=3\\z=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x=8\\y=3\\z=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=3\\z=5\end{matrix}\right.\)

Thay vào S ta có:

\(S=\left(4-4\right)^{2023}+\left(3-4\right)^{2025}+\left(5-4\right)^{2027}=0-1+1=0\)

Câu 1: Đơn thức là: \(3xy^2z^3\)

⇒ Chọn D

Câu 2: Hai đơn thức đồng dạng là: \(\dfrac{1}{2}x^2y^2\) và \(-3x^2y^2\)

⇒ Chọn C 

Câu 3: Hằng đẳng thức là: \(3\left(x+y\right)=3x+3y\)

⇒ Chọn B

Câu 4: \(x^2-...=\left(x-4\right)\left(x+4\right)\Rightarrow x^2-...=x^2-4^2\text{⇒}...=4^2=16\)

⇒ Chọn A

\(A=8.\left(3^2+1\right)\left(3^4+1\right)....\left(3^{16}+1\right)\\ =\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)....\left(3^{16}+1\right)\\ =\left(3^4-1\right)\left(3^4+1\right)....\left(3^{16}+1\right)\\ =\left(3^8-1\right)....\left(3^{16}+1\right)\\ =\left(3^{16}-1\right)\left(3^{16}+1\right)\\ =3^{32}-1\)

A = 8.(3² + 1)(3⁴ + 1)(3⁸ + 1)(3¹⁶ + 1)

= (3² - 1)(3² + 1)(3⁴ + 1)(3⁸ + 1)(3¹⁶ + 1)

= (3⁴ - 1)(3⁴ + 1)(3⁸ + 1)(3¹⁶ + 1)

= (3⁸ - 1)(3⁸ + 1)(3¹⁶ + 1)

= (3¹⁶ - 1)(3¹⁶ + 1)

= 3³² - 1

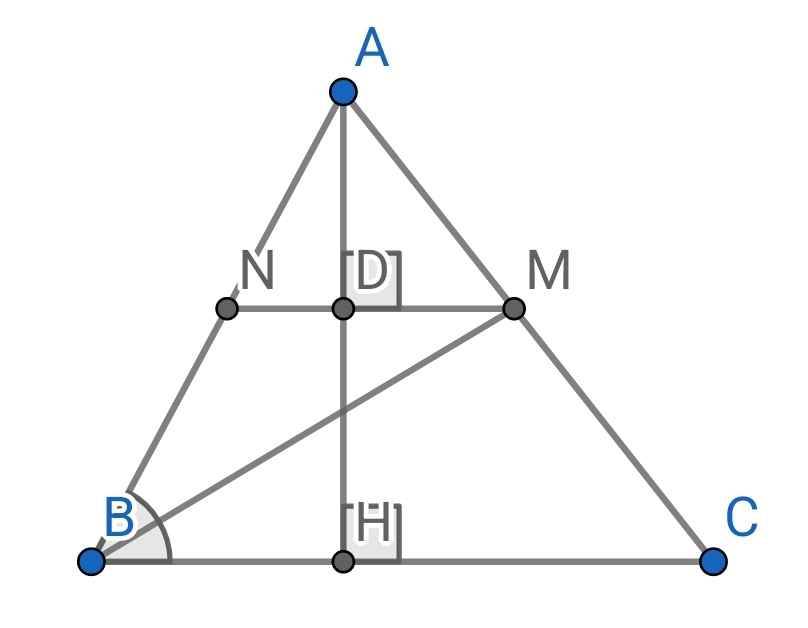 a) Ta có:

AH là đường cao của ∆ABC (gt)

⇒ AH ⊥ BC

Lại có:

MN ⊥ AH (gt)

⇒ MN // BC

Tứ giác BCMN có:

MN // BC (cmt)

⇒ BCMN là hình thang

b) Do MN // BC (cmt)

⇒ ∠NMB = ∠MBC (so le trong)

Do BM là tia phân giác của ∠ABC (gt)

⇒ ∠ABM = ∠MBC

⇒ ∠NBM = ∠MBC

Mà ∠NMB = ∠MBC (cmt)

⇒ ∠NBM = ∠NMB

∆BMN có:

∠NBM = ∠NMB (cmt)

⇒ ∆BMN cân tại N

⇒ BN = MN

M=(a+b)(a²-ab+b²)+3ab(1-2ab)+6a²b²

M=a²-ab+b²+3ab

M=(a+b)²=1

có đáp án chx để mik giải

Lời giải:

$A=(9x^2+6xy+y^2)+y^2-6x+4y+17$

$=(3x+y)^2-2(3x+y)+y^2+6y+17$

$=(3x+y)^2-2(3x+y)+1+(y^2+6y+9)+7$

$=(3x+y-1)^2+(y+3)^2+7\geq 0+0+7=7$

Vậy GTNN của biểu thức là $7$. Giá trị này đạt được khi $3x+y-1=y+3=0$

$\Leftrightarrow y=-3; x=\frac{4}{3}$

$A$ không có max bạn nhé.

Giải:

a, đa thức tính diện tích mảnh đất trồng rau là:

       S = \(x.x\) (m²)

        S = \(x^2\)   (m²)

b,Theo bài ra ta có: \(x^2\) = 96

                           \(\)  \(\left[{}\begin{matrix}x=4\sqrt{6}\\x=-4\sqrt{6}\end{matrix}\right.\)

                            Vì \(x\) > 0 nên \(x\) = 4\(\sqrt{6}\)

Kết luận: cạnh của khu vườn có độ dài là: 4\(\sqrt{6}\)(m)