Lời giải:

Nửa chu vi hình chữ nhật là: $68:2=34$ (m) 

Chiều rộng hcn: $(34-16):2=9$ (m) 

Chiều dài hcn: $9+16=25$ (m) 

Diện tích hcn: $9\times 25=225$ (m²)

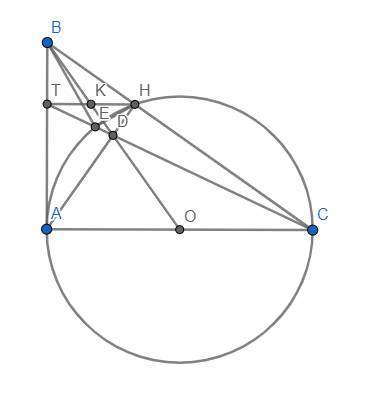
 Gọi T là giao điểm của CD và AB. Khi đó xét tứ giác ACHT, ta có:

O (trung điểm AC), D (giao điểm của 2 đường chéo) và B (giao điểm của 2 đường thẳng chứa 2 cạnh đối) thẳng hàng nên ACHT là hình thang. (bổ đề hình thang quen thuộc)

 \(\Rightarrow\) HT//AC \(\Rightarrow\) H, K, T thẳng hàng.

 Lại có \(\widehat{CEH}=\widehat{CAH}\) (góc nội tiếp cùng chắn cung AH)

 Mà \(\widehat{CAH}=\widehat{B}\) (cùng phụ với góc C)

 \(\Rightarrow\widehat{CEH}=\widehat{B}\)

 \(\Rightarrow\) Tứ giác BTEH nội tiếp \(\Rightarrow\widehat{BEH}=\widehat{BTH}\)

Mà \(\widehat{BTH}=90^o\) nên \(\widehat{BEH}=90^o\). Ta có đpcm.

3A = 3+3²+3³+3⁴+...+3²⁰+3²¹

3A - A = (3+3²+3³+3⁴+...+3²⁰+3²¹) - ( 1+3+3²+3³+...+3¹⁹+2²⁰)

2A = 3²¹-1

A   =  \(\dfrac{31^{21}-1}{2}\)

Vì mỗi hàng có số học sinh giỏi các môn như nhau nên số học sinh mỗi hàng là ước chung của: 96; 120; 72;

Để số hàng ít nhất có thể thì số học sinh mỗi hàng phải lớn nhất có thể.

 Vậy số học sinh mỗi hàng là ước chung lớn nhất của 96; 120; 72

   96 =  2⁵.3;  120 = 2³.3.5;  72 = 2³.3²; ƯCLN(96;120;72) = 2³.3 = 24

  Số hàng dọc của các học sinh giỏi văn là: 96 : 24 = 4 (hàng)

  Số hàng dọc của các học sinh giỏi toán là: 120 : 24 = 5 (hàng)

 Số hàng dọc của các học sinh giỏi ngoại ngữ là: 72 : 24 = 3 (hàng)

   Vậy có thể phân công học sinh đứng thành ít nhất số hàng là:

              4 + 5 + 3 =  12 (hàng)

olm chào em, cảm ơn em đã đồng hành cùng olm trong suốt thời gian qua. Khi em cần trợ giúp thì em đăng nội dung câu hỏi lên diễn đàn olm để được giúp đỡ em nhé. Chúc em luôn có những giây phút học tập thú vị và hiệu quả cùng olm. Thân mến!

Viết bài văn biểu cảm về nhân vật bạch tuộc trong vb bạch tuộc lớp 7

Ai giúp mình với ạ !!! :))

Tổng ba con nặng số ki-lo-gam là:

\(24+32+15=71\left(kg\right)\)

Đáp số: 71 kg 

1 cm = 10 mm 

232 km = 23200000 cm 

23 m = 2300 cm 

1cm=10mm

232km=23200000cm

23m= 2300cm

a : 15 dư 8; a : 35 dư 13 và 200 < a < 300

Vì a : 15 dư 8 nên a = 15k + 8; k\(\in\)N 

 ⇒ 200 < 15k < 300; k \(\in\) N

⇒ 13,3 < k < 20; k \(\in\) N ⇒ k \(\in\){14; 15; 16; 17; 18; 19} (1)

Mặt khác ta có: (15k + 8 - 13) ⋮ 35

                    ⇒ (15k - 5) ⋮ 35

                    ⇒ 5.(3k - 1)⋮ 35

                     ⇒ (3k - 1)⋮ 7

    ⇒ 3k - 1 \(\in\) B(7) = {0; 7; 14; 21; 28; 35; 42; 49; 56; 63;..}

    ⇒ k \(\in\) {\(\dfrac{1}{3}\); \(\dfrac{8}{3}\); \(\dfrac{13}{3}\); \(\dfrac{22}{3}\); \(\dfrac{29}{3}\); 12; \(\dfrac{43}{3}\); \(\dfrac{50}{3}\);19;\(\dfrac{64}{3}\);...;} (2)

Kết hợp (1) và (2) ta có:  k =19

Thay k = 19 vào biểu thức: a = 15k+8 ta có

a = 15.19 + 8 

a = 293

Kết luận số tự nhiên thỏa mãn đề bài là: 293

Cách hai:

Vì a : 15 dư 8 và chia 35 dư 13 nên khi ta thêm 22 đơn vị thì a chia hết cho cả 15 và 35

Ta có: \(\left\{{}\begin{matrix}a+22⋮15\\a+22⋮35\end{matrix}\right.\) ⇒ a + 22 \(\in\) BC(15; 35)  (200 <a<300; a\(\in\)N)

⇒ 222 < a + 22 < 322

15 = 3.5; 35 = 5.7 ⇒ BCNN(15; 35) = 3.5.7 = 105

BC(15; 35) = {0; 105; 210; 315;...}

mà 222 < a + 22 < 322 và a \(\in\) BC(15;35) 

⇒ a + 22 = 315

 ⇒ a = 315 - 22

  ⇒ a =  293

Kết luận: Vậy số tự nhiên thỏa mãn yêu cầu đề bài là 293