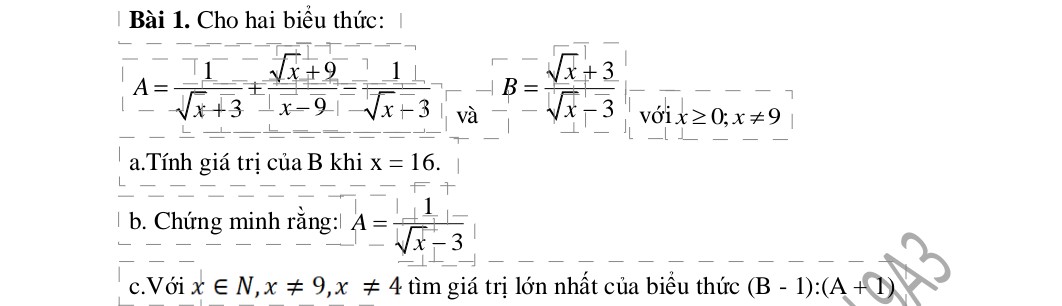
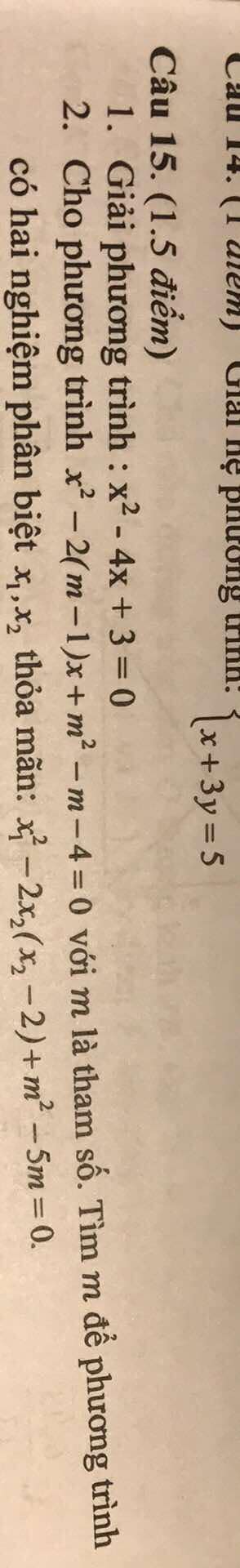Sau khi thống kê độ dài (đơn vị: centimét) của $60$ lá dương xỉ trưởng thành, người ta có bảng tần số ghép nhóm như sau:
| Nhóm | $[10; 20)$ | $[20; 30)$ | $[30; 40)$ | $[40; 50)$ | Tổng |
| Tần số | $8$ | $18$ | $24$ | $10$ | $60$ |
a) Tìm tần số tương đối của mỗi nhóm đó.
b) Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó.
c) Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm đó.