Gọi 2 số nguyên tố đó là p, q và giả sử \(p>q\). Khi đó ta có \(p+q,p-q\) đều là các số nguyên tố.

 Nếu \(p-q=2\) \(\Rightarrow p+q=2\) (vì \(\left(p-q\right)+\left(p+q\right)=2p⋮2\)), vô lí

 Tương tự với TH \(p+q=2\) cũng sẽ dẫn tới điều vô lí.

 Do đó \(p+q,p-q\) lẻ, mà p và q đều các số nguyên tố \(\Rightarrow q=2\)

 Vậy, ta cần tìm p để \(p\pm2\) là các số nguyên tố \(\Rightarrow p\ge5\)

 Xét \(p=5\) thì \(p+2=7;p-2=3\) thỏa mãn.

 Xét \(p>5\) thì p có dạng \(p=6k+1,p=6k+5\left(k\ge1\right)\), khi đó dễ thấy rằng \(p+2,p-2\) là hợp số, vô lí.

 Vậy \(p=5,q=2\) là cặp số nguyên tố duy nhất thỏa mãn đề bài.

5 + 2 = 7

5 - 2 = 3

Hai số đó là 2 và 5

88= 11.2³ ; 156=2².3.13

Gọi a là số nhóm tối đa chia được (a: nguyên, dương)

Vậy a=ƯCLN(88;156)= 2²=4

 Vậy có thể chia tối đa 4 nhóm tình nguyện, mỗi nhóm có 22 nam và 39 nữ , tổng cộng là 61 người

88= 11.23 ; 156=22.3.13

Gọi a là số nhóm tối đa chia được (a: nguyên, dương)

Vậy a=ƯCLN(88;156)= 22=4

 Vậy có thể chia tối đa 4 nhóm tình nguyện

34842

\(\text{9755,9657 + 6776,8654 = 16532,8311}\)

??????????????????????????????????????????????????????????????????????????????????????????????????????????????????

☹

1963+1964+1965+1966+1967+.......+2021+2022+2023
Gọi A = 1963+1964+1965+1966+1967+.......+2021+2022+2023

 Số số hạng của S là: 

 \(\dfrac{2023-1963}{1}+1=71\left(\text{Số số hạng}\right)\) 

Tổng của A là:

\(\dfrac{\left(2023+1963\right).71}{2}=141503\)

Vậy tổng của 1963+1964+1965+1966+1967+...+2021+2022+2023+2024 = 141503

toán lớp 1 haha

a) 1/4(x-3)+2=1/5

1/4.(x-3) = 1/5-2

1/4.(x-3) = -9/5

x-3 = (-9/5):1/4

x-3 = -36/5

x = -36/5+3

x= -21/5

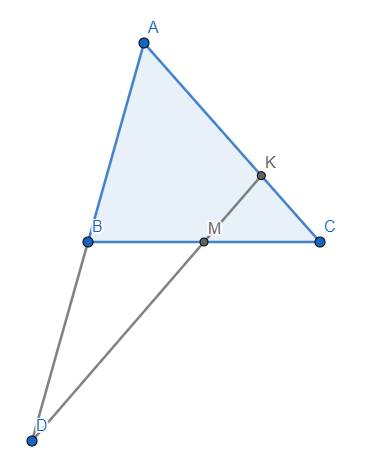
 Bài này có thể giải bằng cách dùng định lý Menelaus khá ngắn như sau:

 Áp dụng định lý Menelaus cho tam giác ABC với cát tuyến DMK, ta có: \(\dfrac{MB}{MC}.\dfrac{KC}{KA}.\dfrac{DA}{AB}=1\) \(\Rightarrow1.\dfrac{KC}{KA}.2=1\) \(\Leftrightarrow\dfrac{KC}{KA}=\dfrac{1}{2}\) \(\Leftrightarrow KA=2KC\) (đpcm)

 Nhưng nếu bạn chưa được dùng định lý Menelaus thì sẽ phải làm như sau:

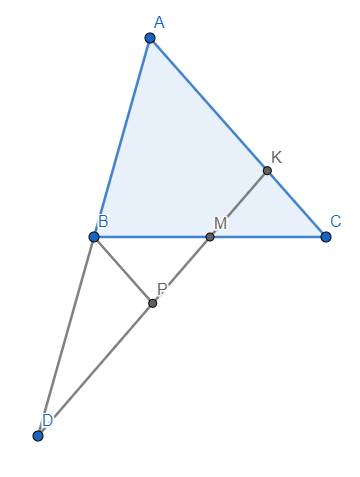
 Kẻ BP//AC \(\left(P\in DK\right)\). Khi đó theo định lý Thales, \(\dfrac{MB}{MC}=\dfrac{BP}{CK}\) và \(\dfrac{DA}{DB}=\dfrac{AK}{BP}\). Do đó:

 \(\dfrac{MB}{MC}.\dfrac{KC}{KA}.\dfrac{DA}{DB}=\dfrac{BP}{CK}.\dfrac{CK}{AK}.\dfrac{AK}{BP}=1\), và tới đây ta lại quay về tính như đã trình bày ở trên.

Lời giải:
Gọi $d=ƯCLN(a,b)$ thì đặt $a=dx, b=dy$ với $x,y$ là stn>0 và $(x,y)=1$.

Khi đó: $BCNN(a,b)=dxy$

Theo bài ra ta có:

$d+dxy=19$

$\Rightarrow d(1+xy)=19$

Vì $1+xy>1$ với mọi $x,y\in\mathbb{N}^*$ nên $1+xy=19; d=1$

$\Rightarrow xy=18; d=1$

Vì $(x,y)=1, a< b\Rightarrow x<y$

$\Rightarrow x=2, y=9$

$\Rightarrow a=dx=1.2=2; b=1.9=9$

Tổng của ba số:

30 × 3 = 90

Số A là:

A = 90 - 20 - 45 = 25

Tổng của ba số:

30 × 3 = 90

Số A là:

A = 90 - 20 - 45 = 25