P = \(\dfrac{3x+2}{4x-5}\) Đk \(x\ne\) \(\dfrac{5}{4}\)

P \(\in\) Z ⇔ 3\(x\) + 2 ⋮ 4\(x\) - 5 

        (3\(x\) + 2).4 ⋮ 4\(x\) - 5

        12\(x\) + 8    ⋮ 4\(x\) - 5

  3.(4\(x\) - 5) + 23 ⋮ 4\(x\) - 5

        23 ⋮ 4\(x\) - 5

    4\(x\) - 5 \(\in\) Ư(23) = {-23; -1; 1; 23}

    \(x\) \(\in\) {- \(\dfrac{9}{2}\); 1; \(\dfrac{3}{2}\); 7}

Vì \(x\in\) Z nên \(x\) \(\in\) {1; 7}

Lời giải:

Nếu y chẵn thì y=2. Khi đó: $x^2=2y^2+1=2.2^2+1=9\Rightarrow y=3$ 

Nếu $y$ lẻ: 

Ta biết rằng 1 scp khi chia 8 có dư 0,1,4 nên với $y$ lẻ suy ra $y^2$ chia $8$ dư $1$
$\Rightarrow x^2=2y^2+1$ chia $8$ dư $2.1+1=3$
(vô lý vì $x^2$ là scp nên không thể chia 8 dư 3)

Vậy $(x,y)=(3,2)$

\(\sqrt{0,36}+5\sqrt{1,21}=0,6+5.1,1=0,65,5=6,1\)

- Bởi vì có những nhóm chất tuy không tạo ra năng lượng nhưng lại có các chức năng khác quan trọng đối với cơ thể. Như giúp tăng cường đề kháng, ngăn ngừa các bệnh tật. 

- Và các nhóm chất này có 1 số ít cơ thể không tạo ra được và cần bổ sung từ thực phẩm. 

giúp trả lời câu này

\(\sqrt{\dfrac{25}{4}}-\sqrt{\dfrac{49}{16}}=\dfrac{5}{2}-\dfrac{7}{4}=\dfrac{10}{4}-\dfrac{7}{4}=\dfrac{3}{4}\)

căn 25/4-căn 49/16=căn(5/2)mũ 2-căn(7/4)mũ 2=5/2-7/4=3/4

Lời giải:
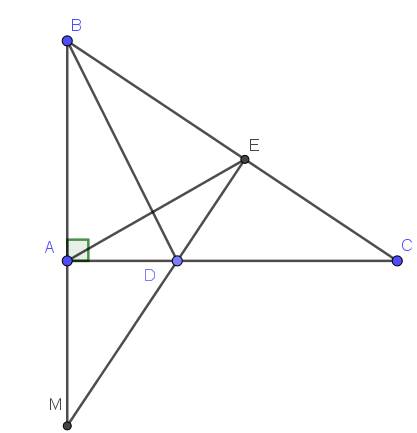
a. Xét tam giác $ABD$ và $EBD$ có:

$AB=EB$ 

$BD$ chung

$\widehat{ABD}=\widehat{EBD}$ (do $BD$ là phân giác $\widehat{B}$)

$\Rightarrow \triangle ABD=\triangle EBD$ (c.g.c)

b.

Từ tam giác bằng nhau phần a suy ra:

$AD=DE$

$\widehat{BED}=\widehat{BAD}=90^0$

$\Rightarrow DE\perp BC$

$\Rightarrow \widehat{DEC}=90^0$
Xét tam giác $ADM$ và $EDC$ có:

$AD=ED$ (cmt)

$\widehat{ADM}=\widehat{EDC}$ (đối đỉnh)

$\widehat{DAM}=\widehat{DEC}=90^0$

$\Rightarrow \triangle ADM=\triangle EDC$ (g.c.g)

$\Rightarrow AM=EC$

c.

Từ tam giác bằng nhau phần b suy ra:

$\widehat{M_1}=\widehat{C_1}$

$DM=DC$

Mà $DE=AD$

$\Rightarrow DM+DE=DC+AD$

$\Rightarrow ME=AC$

Xét tam giác $AEM$ và $EAC$ có:

$AM=EC$ (cmt)

$EM=AC$ (cmt)

$\widehat{M_1}=\widehat{C_1}$ (cmt)

$\Rightarrow \triangle AEM=\triangle EAC$ (c.g.c)

$\Rightarrow \widehat{EAM}=\widehat{AEC}$

Hình vẽ:

7\(x\) - 2y = 15

y =( 7\(x\) - 15) : 2

⇒ 7\(x\) - 15 ⋮ 2

⇒ \(x\) - 1 ⋮ 2 

⇒ \(x\) = 2k + 1; k \(\in\) N

    Vì y là số tự nhiên nên 7\(x\) - 15 ≥ 0 ⇒ \(x\) ≥ \(\dfrac{15}{7}\) 

  ⇒ 2k + 1 ≥ \(\dfrac{15}{7}\)

       k ≥ (\(\dfrac{15}{7}\) - 1 ) : 2

     k ≥ \(\dfrac{8}{14}\) ⇒ k ≥ 1;

⇒ \(x\) = 2k + 1; k ϵ N*

y = \(\dfrac{7.\left(2k+1\right)-15}{2}\)

y = 7k - 4

Vậy câc cặp số tự nhiên \(x;y\) thỏa mãn đề bài là

(\(x;y\)) = (2k+1; 7k - 4); k \(\in\)N*

\(\left(\dfrac{-3}{4}\right)^2.\left(\dfrac{-6}{9}\right)^2\)

\(=\left(\dfrac{-3}{4}.\dfrac{-6}{9}\right)^2\)

\(=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)

*Công thức: \(a^m.b^m=\left(a.b\right)^m\)

\(#Thitottt:3\)

\(CTTQ:H_xS_y\left(x,y:nguyên,dương\right)\\ M_{H_xS_y}=17M_{H_2}=17.2=34\left(\dfrac{g}{mol}\right)\\ x=\dfrac{5,88\%.34}{1}=2;y=\dfrac{34-2.1}{32}=1\\ \Rightarrow CTPT:H_2S\)