Cho hai số có tổng là 126. Biết rằng nếu lấy số lớn trừ đi số bé rồi cộng với tổng
của chúng thì được 144
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

27 x 25 x 29 x a = \(\overline{3b2350}\)
Vì 27 ⋮ 9 nên \(\overline{3b2350}\) ⋮ 9
Vậy 3 + b + 2 + 3 + 5 ⋮ 9
13 + b ⋮ 9
b = 5
27 x 25 x 29 x a = 352350
19575 x a = 352350
a = 352350 : 19575
a = 18
Vậy a = 18; b = 5

Diện tích xung quanh căn phòng:
\(\left(8+4,5\right)\times2\times4=100\left(m^2\right)\)
Diện tích cần quét vôi:
\(100\times2-6=194\left(m^2\right)\)
Đáp số: 194 m2
Giải:
Diện tích vôi cần quét cả mặt trong và ngoài của căn phòng là:
\(\left[\left(8+4,5\right)\times2\times4\right]\times2=200\left(m^2\right)\)
Diện tích vôi cần quét là cần quét là:
\(200-6=194\left(m^2\right)\)
Đáp số: \(194\text{ }m^2\)

Tính tổng của Chiều dài, Chiều rộng = (Diện tích x 2 : Chiều cao)
(Còn cách tính Chiều dài, Chiều rộng thì tuỳ đề bài mà tìm bạn nhé)

Lời giải:
a. Chiều rộng bể cá: $1,2\times \frac{2}{3}=0,8$ (m)
Chiều cao bể cá: $0,8\times \frac{2}{3}=\frac{8}{15}$ (m)
Thể tích bể:
$1,2\times 0,8\times \frac{8}{15}=0,512$ (m3)
b.
Nếu 15% bể không chứa nước thì bể chứa số lít nước là:
0,512\times (100-15)\times 100=0,4352$ (m3) = 435,2 lít

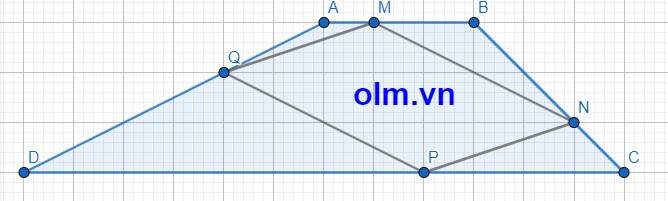
\(\dfrac{AM}{AB}\) = \(\dfrac{1}{1+2}\) = \(\dfrac{1}{3}\)
SAMQ = \(\dfrac{1}{3}\) SABQ (vì hai tam giác có chung chiều cao hạ từ đỉnh Q xuống đáy AB và AM = \(\dfrac{1}{3}\)AB)
\(\dfrac{AQ}{AD}\) = \(\dfrac{1}{1+2}\) = \(\dfrac{1}{3}\)
SABQ = \(\dfrac{1}{3}\)SABD (Vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AD và AQ = \(\dfrac{1}{3}\)AD)
SAQM = \(\dfrac{1}{3}\)\(\times\)\(\dfrac{1}{3}\)SABD = \(\dfrac{1}{9}\)SABD
\(\dfrac{BN}{BC}\) = \(\dfrac{2}{2+1}\) = \(\dfrac{2}{3}\)
\(\dfrac{BM}{AB}\) = \(\dfrac{2}{2+1}\) = \(\dfrac{2}{3}\)
Chứng minh tương tự ta có:
SBMN = \(\dfrac{2}{3}\)\(\times\)\(\dfrac{2}{3}\)SABC = \(\dfrac{4}{9}\)SABC
\(\dfrac{CN}{CB}\) = \(\dfrac{1}{2+1}\) = \(\dfrac{1}{3}\)
\(\dfrac{CP}{CD}\) = \(\dfrac{1}{2+1}\) = \(\dfrac{1}{3}\)
Chứng minh tương tự ta có:
SCPN = \(\dfrac{1}{3}\) \(\times\) \(\dfrac{1}{3}\)SBCD = \(\dfrac{1}{9}\)SBCD
\(\dfrac{DQ}{AD}\) = \(\dfrac{2}{2+1}\) = \(\dfrac{2}{3}\)
\(\dfrac{DP}{DC}\) = \(\dfrac{2}{2+1}\) = \(\dfrac{2}{3}\)
Chứng minh tương tự ta có:
SDPQ = \(\dfrac{2}{3}\) \(\times\) \(\dfrac{2}{3}\)SABD = \(\dfrac{4}{9}\)SADC
SAMQ + SBMN + SCNB + SDPQ = \(\dfrac{1}{9}\)SABD+\(\dfrac{4}{9}\)SABC+\(\dfrac{1}{9}\)SBCD+\(\dfrac{4}{9}\)SADC = \(\dfrac{5}{9}\)SABCD
SMNPQ = SABCD - \(\dfrac{5}{9}\)SABCD = \(\dfrac{4}{9}\)SABCD = 360 x \(\dfrac{4}{9}\) = 160 (cm2)
Đs:...
bang1