CÓ 128 CON CHÓ VÀ 128 CON MÈO . HỎI CẢ CHÓ VÀ MÈO CÓ TẤT CẢ BAO NHIÊU CÁI CHÂN?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


vì mỗi con mèo có 4 cái chân nên
số chân của 33 con mèo là:
33×4 =132 ( cái )
Số chân của 33 con mèo là:
\(33\times4=132\left(chan\right)\)

B(x) = x2+x
Đặt B(x) = 0
=> x2+x=0
x.x + x = 0
x(x+1)=0
TH1: x = 0
TH2: x+1 = 0
x = -1
Vậy nghiệm của B(x) là x=-1

Cho n(x) = 0
5x² + 9x + 4 = 0
5x² + 5x + 4x + 4 = 0
(5x² + 5x) + (4x + 4) = 0
5x(x + 1) + 4(x + 1) = 0
(x + 1)(5x + 4) = 0
*) x + 1 = 0
x = 0 - 1
x = -1
*) 5x + 4 = 0
5x = 0 - 4
5x = -4
x = -4/5
Vậy nghiệm của đa thức n(x) là x = -1; x = -4/5
Cho \(n\left(x\right)=0\) \(\Leftrightarrow5x^2+9x+4=0\)
\(\Leftrightarrow5x^2+5x+4x+4=0\)
\(\Leftrightarrow5x\left(x+1\right)+4\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(5x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{4}{5}\end{matrix}\right.\)
Như vậy n(x) có 2 nghiệm là \(-1\) và \(-\dfrac{4}{5}\)

a, Tổng A có 11 số hạng
( Nhìn từ 21 đến 210 thấy được 10 số, thêm số 1 nữa => 11 số hạng )
b,
\(A=1+2^1+2^2+...+2^9+2^{10}\)
\(\Rightarrow2A=2+2^2+2^3+...+2^{10}+2^{11}\)
Ta có \(2A-A=\left(2+2^2+...+2^{11}\right)-\left(1+2^1+..+2^{10}\right)\)
\(\Leftrightarrow\)\(A\)\(=2^{11}-1\)
mà \(2^{11}-1< 2^{11}\)
hay \(A< 2^{11}\)
`@` `\text {Ans}`
`\downarrow`
`a,`
Số hạng của tổng A là:
`(10 - 1) \div 1 + 1 + 1 = 11 (\text {số hạng})`
`b,`
`A = 1+2^1+2^2+2^3+...+2^9+2^10`
`2A = 2(1+2+2^2+...+2^9+2^10)`
`2A = 2+2^2+2^3+...+2^10+2^11`
`2A - A = (2+2^2+2^3+...+2^10+2^11) - (1+2^1+2^2+2^3+...+2^9+2^10)`
`A = 2^11 - 1`
Vì `2^11 - 1 < 2^11`
`-> A < 2^11`
Vậy:
`a,` `11` số hạng *Mình dùng lũy thừa để tính á cậu;-;*
`b,` `A < 2^11.`

\(5^{n+1}+5^n=6\cdot125\)
`-> 5^n*5+5^n=750`
`-> 5^n(5+1)=750`
`-> 5^n*6=750`
`-> 5^n = 125`
`-> 5^n = 5^3`
`-> n=3`

Viết từ 1 đến 999 thì các số có chữ số ở hàng đơn vị có dạng:
\(\overline{a0}\); \(\overline{bc0}\).
Xét các số có dạng \(\overline{a0}\), \(a\) có 9 cách chọn vậy có 9 số
Xét các số có dạng \(\overline{bc0}\), \(b\) có 9 cách chọn; \(c\) có 10 cách chọn vậy có:
9 \(\times\) 10 = 90 (số)
Các số có chữ số 0 ở hàng chục có dạng: \(\overline{d0e}\)
\(d\) có 9 cách chọn. \(e\) có 10 cách chọn vậy có:
9 \(\times\) 10 = 90 (số)
Từ những lập trên cho thấy viết liên tiếp các số tự nhiên từ 1 đến 999 thì chữ số 0 xuất hiện số lần là:
9 + 90 + 90 = 189 (lần)
Đáp số: 189 lần

Bài 2:
Q(\(x\)) = 2\(x^2\) + 3\(x\) - 4\(x^2\) + \(x\) + 1
Q(\(x\)) = -(4\(x^2\) - 2\(x^2\)) + (3\(x\) + \(x\)) + 1
Q(\(x\)) = -2\(x^2\) + 4\(x\) + 1
Bài 3:
P(\(x\)) = \(x^3\) + 2 Và Q(\(x\)) = \(x^3\) - \(x^2\) - 2
P(\(x\)) - Q(\(x\)) = \(x^3\) + 2 - (\(x^3\) - \(x^2\) - 2)
P(\(x\)) - Q(\(x\)) = \(x^3\) + 2 - \(x^3\) + \(x^2\) + 2
P(\(x\)) - Q(\(x\)) = (\(x^3\) - \(x^3\)) + \(x^2\) + (2 + 2)
P(\(x\)) - Q(\(x\)) = 0 + \(x^2\) + 4
P(\(x\)) - Q(\(x\)) = \(x^2\) + 4
1) Q(x)=2x2+3x-4x2+x+1
=-2x2+4x+1
2) P(x)-Q(x)= (x3+2)-(x3-x2-2)
=x3+2-x3+x2+2
=4+x2
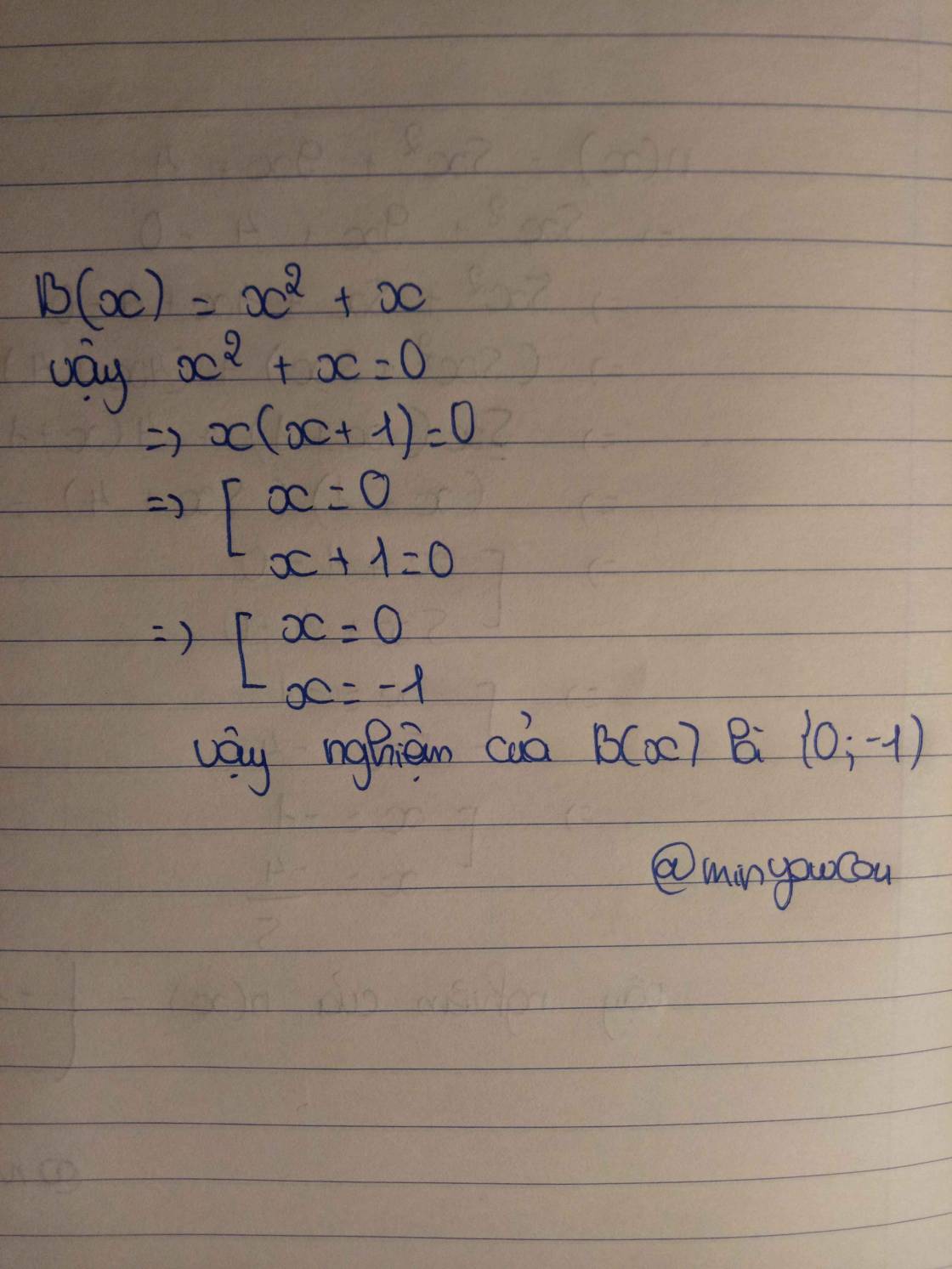
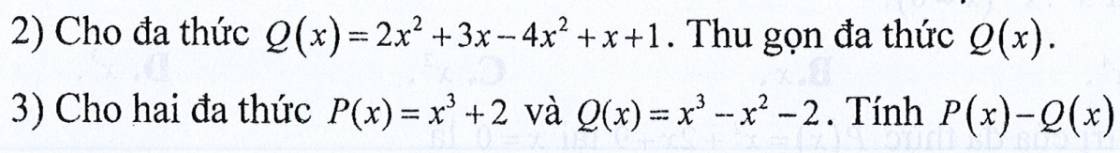
Số chân chó là:
\(128\times4=512\left(chan\right)\)
Số chân mèo:
\(128\times4=512\left(chan\right)\)
Tổng chân chó và chân mèo:
\(512+512=1024\left(chan\right)\)
Cả chó và mèo có tất cả số chân là:
128+128=256(cái)