a) Xét hai tam giác vuông: ∆AHC và ∆MHC có:

HC là cạnh ccung

AH = MH (gt)

⇒ ∆AHC = ∆MHC (hai cạnh góc vuông)

b) Do ∆AHC = ∆MHC (cmt)

⇒ ∠ACH = ∠MCH (hai góc tương ứng)

AC = MC (hai cạnh tương ứng)

Do ∠ACH = ∠MCH (cmt)

⇒ ∠ACB = ∠MCB

Xét ∆ABC và ∆MBC có:

AC = MC (cmt)

∠ACB = ∠MCB (cmt)

BC là cạnh chung

⇒ ∆ABC = ∆MBC (c-g-c)

Mặt trống rung động làm cho không khí xung quanh cũng rung động. Rung động này lan truyền trong không khí. Khi rung động lan truyền tới miệng ống sẽ làm cho tấm ni lông rung động và làm cho các mẩu giấy chuyển động. Tương tự như vậy, khi rung động lan truyền tới tai ta, sẽ làm màng nhĩ rung động, nhờ đó ta có thể nghe được âm thanh.

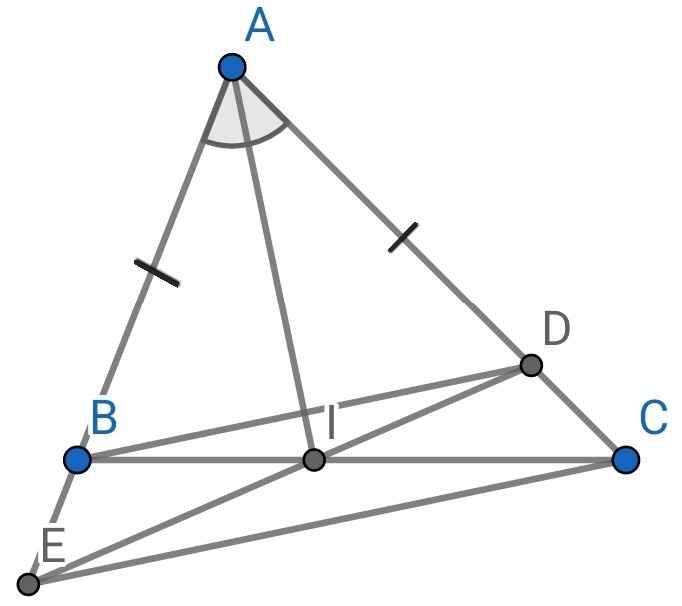
a) Do AI là tia phân giác của BAC (gt)

⇒ ∠BAI = ∠CAI

⇒ ∠BAI = ∠DAI

Xét ∆BAI và ∆DAI có:

AB = AD (gt)

∠BAI = ∠DAI (cmt)

AI là cạnh chung

⇒ ∆BAI = ∆DAI (c-g-c)

⇒ BI = ID (hai cạnh tương ứng)

b) Do ∆BAI = ∆DAI (cmt)

⇒ ∠ABI = ∠ADI (hai góc tương ứng)

Mà ∠ABI + ∠EBI = 180⁰ (kề bù)

∠ADI + ∠CDI = 180⁰ (kề bù)

⇒ ∠EBI = ∠CDI

Xét ∆IBE và ∆IDC có:

∠EBI = ∠CDI (cmt)

BI = ID (cmt)

∠BIE = ∠DIC (đối đỉnh)

⇒ ∆IBE = ∆IDC (g-c-g)

c) Do ∆IBE = ∆IDC (cmt)

⇒ BE = DC (hai cạnh tương ứng)

Mà AB = AD (gt)

⇒ AE = AB + BE = AD + DC = AC

∆AEC có:

AE = AC (cmt)

⇒ ∆AEC cân tại A

⇒ ∠AEC = (180⁰ - ∠EAC) : 2    (1)

∆ABD có:

AB = AD (gt)

⇒ ∆ABD cân tại A

⇒ ∠ABD = (180⁰ - ∠BAD) : 2 = (180⁰ - ∠EAC) : 2   (2)

Từ (1) và (2) ⇒ ∠AEC = ∠ABD

Mà ∠AEC và ∠ABD là hai góc đồng vị

⇒ BD // EC

Lời giải:
Đặt $\frac{a_1}{a_2}=\frac{a_2}{a_3}=\frac{a_3}{a_4}=...=\frac{a_n}{a_{n+1}}=t$

Áp dụng TCDTSBN:

$t=\frac{a_1}{a_2}=\frac{a_2}{a_3}=\frac{a_3}{a_4}=...=\frac{a_n}{a_{n+1}}=\frac{a_1+a_2+a_3+....+a_n}{a_2+a_3+....+a_{n+1}}$

$\Rightarrow t^n=\left[\frac{a_1+a_2+a_3+....+a_n}{a_2+a_3+....+a_{n+1}}\right]^n(*)$

Lại có:

$\frac{a_1}{a_2}.\frac{a_2}{a_3}.\frac{a_3}{a_4}....\frac{a_n}{a_{n+1}}=t.t.t....t$

$\Rightarrow \frac{a_1}{a_{n+1}}=t^n(**)$
Từ $(*)$ và $(**)$ ta có:

$\left[\frac{a_1+a_2+a_3+....+a_n}{a_2+a_3+....+a_{n+1}}\right]^n=\frac{a_1}{a_{n+1}}$ (đpcm)

Lời giải:

Số học sinh khá giỏi chiếm số phần trăm số hs cả lớp là:

$100-50=50$ (%)

Tổng số học sinh khá giỏi là: $10+15=25$ (hs)

Số học sinh cả lớp là: $25:50\times 100=50$ (hs) 

Số học sinh trung bình: $50\times 50:100=25$ (hs)

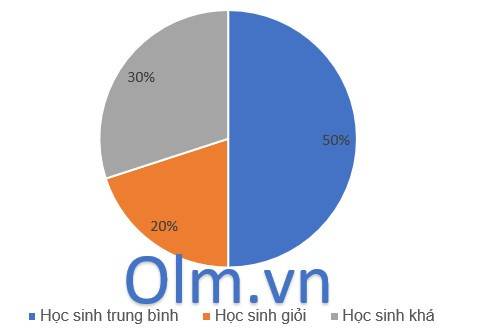
a;Số học sinh giỏi và khá so với số học sinh cả lớp chiếm số phần trăm là:    

                   100% - 50% = 50%

 50% ứng với số học sinh là:   10 + 15 = 25 (học sinh)

 Số học sinh cả lớp là:    25 : 50 x 100 = 50 (học sinh)

Số học sinh trung bình là: 50 - 25 = 25 (học sinh)

Số học sinh khá chiếm số phần trăm là: 15 : 50 x 100% = 30%

Số học sinh giỏi chiếm số phần trăm là: 100% - 50% - 30% = 20%

b, Ta có biểu đồ hình quạt tròn dưới đây