Tính giá trị của biểu thức $A=2\sqrt{12}-\sqrt{48}+3\sqrt{27}-\sqrt{108}.$
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


gọi x; y lần lượt là số chi tiết mà tổ 1 và tổ 2 sản xuất trong tháng đầu (ĐK: 0 < x; y < 300)
theo đề 2 tổ sản xuất đc 300 chi tiết nên: x + y = 300 (1)
số chi tiết tổ 1 vượt là: \(x\cdot\left(1+15\%\right)=1,15x\)
số chi tiết tổ 2 vượt là: \(y\cdot\left(1+20\%\right)=1,2y\)
mà cả 2 tổ sản xuất đc 352 chi tiết nên:
\(1,15x+1,2y=352\left(2\right)\)
từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=300\\1,15x+1,2y=352\end{matrix}\right.\)
giải ra ta được: \(\left\{{}\begin{matrix}x=160\left(TM\right)\\y=140\left(TM\right)\end{matrix}\right.\)
vậy tổ 1 sản xuất 160 chi tiết máy trong tháng đầu; tổ 2 sản xuất 140 chi tiết máy trong tháng đầu

a) Tìm \(M\) để đồ thị hàm số \(y = \left(\right. m + 1 \left.\right) x^{2}\) đi qua điểm \(A \left(\right. 2 , 4 \left.\right)\):
Để hàm số \(y = \left(\right. m + 1 \left.\right) x^{2}\) đi qua điểm \(A \left(\right. 2 , 4 \left.\right)\), ta thay giá trị \(x = 2\) và \(y = 4\) vào phương trình hàm số:
\(y = \left(\right. m + 1 \left.\right) x^{2}\)
Thay \(x = 2\) và \(y = 4\):
\(4 = \left(\right. m + 1 \left.\right) \cdot 2^{2}\) \(4 = \left(\right. m + 1 \left.\right) \cdot 4\) \(4 = 4 \left(\right. m + 1 \left.\right)\)
Chia cả hai vế cho 4:
\(1 = m + 1\) \(m = 0\)
Vậy giá trị của \(m\) là 0.
like minh nhe minh lam duoc cau a thôi
Để giải bài toán này, chúng ta sẽ thực hiện từng bước một.
a) Tìm \(m\) để đồ thị hàm số đi qua điểm \(A \left(\right. 2 , 4 \left.\right)\)
- Thay tọa độ điểm A vào hàm số:
Hàm số cho trước là: \(y = \left(\right. m + 1 \left.\right) x^{2}\)Thay \(x = 2\) và \(y = 4\): \(4 = \left(\right. m + 1 \left.\right) \left(\right. 2^{2} \left.\right)\) - Giải phương trình:
Tính giá trị \(2^{2}\): \(2^{2} = 4 \Rightarrow 4 = \left(\right. m + 1 \left.\right) \cdot 4\)Chia cả hai vế cho 4: \(1 = m + 1\)Trừ 1 từ cả hai vế: \(m = 0\)
Kết luận phần a:
- Giá trị của \(m\) là \(0\).
b) Vẽ đồ thị hàm số \(y = \left(\right. m + 1 \left.\right) x^{2}\) với giá trị \(m\) vừa tìm được
- Thay giá trị \(m\) vào hàm số:
Với \(m = 0\): \(y = \left(\right. 0 + 1 \left.\right) x^{2} = x^{2}\) - Xác định các điểm trên đồ thị:
- Khi \(x = - 2\), \(y = \left(\right. - 2 \left.\right)^{2} = 4\)
- Khi \(x = - 1\), \(y = \left(\right. - 1 \left.\right)^{2} = 1\)
- Khi \(x = 0\), \(y = 0^{2} = 0\)
- Khi \(x = 1\), \(y = 1^{2} = 1\)
- Khi \(x = 2\), \(y = 2^{2} = 4\)
- Vẽ đồ thị:
Đồ thị của hàm số \(y = x^{2}\) là một parabol mở lên trên. Các điểm mà chúng ta đã tính sẽ giúp hình dung đồ thị: - Điểm \(\left(\right. - 2 , 4 \left.\right)\)
- Điểm \(\left(\right. - 1 , 1 \left.\right)\)
- Điểm \(\left(\right. 0 , 0 \left.\right)\)
- Điểm \(\left(\right. 1 , 1 \left.\right)\)
- Điểm \(\left(\right. 2 , 4 \left.\right)\)
Kết luận phần b:
- Đồ thị của hàm số \(y = x^{2}\) là một parabol mở lên với đỉnh tại điểm \(\left(\right. 0 , 0 \left.\right)\).
Nếu bạn cần thêm thông tin hoặc có câu hỏi gì khác, hãy cho tôi biết!

Gọi H là giao điểm của BC và AD
D đối xứng A qua BC
=>BC\(\perp\)AD tại H và H là trung điểm của AD
Xét ΔBAD có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔBAD cân tại B
=>BA=BD
Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
DO đó: ΔCAD cân tại C
=>CA=CD
Xét ΔBAC và ΔBDC có
BA=BD
CA=CD
BC chung
Do đó: ΔBAC=ΔBDC
=>\(\widehat{BAC}=\widehat{BDC}=90^0\)
=>ABDC là tứ giác nội tiếp

bàu 1 : gọi v2 (km/h) là vận tốc của xe thứ hai (đk: v1 > v2 > 0)
vận tốc xe 1 sẽ là v1 = v2 + 10 (km/h)
thời gian xe 1 đi từ A -> B: \(t_1=\dfrac{200}{v_1}=\dfrac{200}{v_2+10}\left(h\right)\)
thời gian xe 2 đi từ A -> B: \(t_2=\dfrac{200}{v_2}\left(h\right)\)
theo đề bài, xe thứ nhất đến sớm hơn 1 giờ nên:
\(t_2-t_1=1\Leftrightarrow\dfrac{200}{v_2}-\dfrac{200}{v_2+10}=1\\ =>200\left(v_2+10\right)-200v_2=v_2\left(v_2+10\right)\\ =>200v_2+2000-200v_2=v_2^2+10v_2\\ =>2000=v_2^2+10v_2\\ =>v_2^2+10v_2-2000=0\\ =>\left[{}\begin{matrix}v_2=40\left(km.h\right)\left(TM\right)\\v_2=-50\left(km.h\right)\left(KTM\right)\end{matrix}\right.\)
\(v_1=v_2+10=40+10=50\left(km.h\right)\)
vậy vận tốc xe 1 là 50km/h; vận tốc xe 2 là 40km/h
bài 2: gọi \(t_d\text{ là thời gian dự tính; }t_t\text{ là thời gian thực tế}\)
thời gian người đó dự định đi hết quãng đường là:
\(t_d=\dfrac{90}{v}\left(h\right)\)
1/2 quãng đường là: \(90\cdot\dfrac{1}{2}=45\left(km\right)\)
quãng đường đầu tiên người đó đi: \(t_1=\dfrac{45}{v}\left(h\right)\)
quãng đường còn lại người đó đi: \(t_2=\dfrac{45}{v-10}\left(h\right)\)
thời gian thực tế người đó đi là: \(t_t=\dfrac{45}{v}+\dfrac{45}{v-10}\left(h\right)\)
mà \(t_t=t_d+\dfrac{18}{60}\)
\(=>\dfrac{45}{v}+\dfrac{45}{v-10}=\dfrac{90}{v}+0,3\\ =>\dfrac{45}{v-10}-\dfrac{45}{v}=0,3\\ 45v-45\left(v-10\right)=0,3v\left(v-10\right)\\ 45v-45v+450=0,3v^2-3v\\ =>0,3v^2-3v-450=0\\ < =>v^2-10v-1500=0\\ =>\left[{}\begin{matrix}v\approx44\left(km.h\right)\left(TM\right)\\v\approx-34\left(km.h\right)\left(KTM\right)\end{matrix}\right.\)
thời gian thực tế người đó đi là:
\(t_t=\dfrac{45}{44}+\dfrac{45}{44-10}\approx2,34\left(h\right)=2h20p\)
vậy vận tốc dự đinh là 44km/hl thời gian đi là 2h20p

Gọi vận tốc của cano lúc nước yên lặng là x(km/h)
(Điều kiện: x>4)
vận tốc lúc xuôi dòng là x+4(km/h)
Vận tốc lúc ngược dòng là x-4(km/h)
Thời gian đi xuôi dòng là \(\dfrac{30}{x+4}\left(giờ\right)\)
Thời gian đi ngược dòng là \(\dfrac{30}{x-4}\left(giờ\right)\)
Tổng thời gian cả đi lẫn về là 4 giờ nên ta có:
\(\dfrac{30}{x+4}+\dfrac{30}{x-4}=4\)
=>\(\dfrac{30\left(x-4\right)+30\left(x+4\right)}{\left(x+4\right)\left(x-4\right)}=4\)
=>\(4\left(x^2-16\right)=60x\)
=>\(x^2-16=15x\)
=>\(x^2-15x-16=0\)
=>(x-16)(x+1)=0
=>\(\left[{}\begin{matrix}x-16=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=16\left(nhận\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
Vậy: Vận tốc của cano lúc nước yên lặng là 16km/h

Thời gian(phút) | [0;5) | [0;5) | [0;5) | [0;5) |
Tần số(n) | 9,375% | 9,375% | 9,375% | 9,375% |
biểu đồ của em là :
Thời gian(phút) | [0;5) | [0;5) | [0;5) | [0;5) |
Tần số(n) | 9,375% | 9,375% | 9,375% | 9,375% |

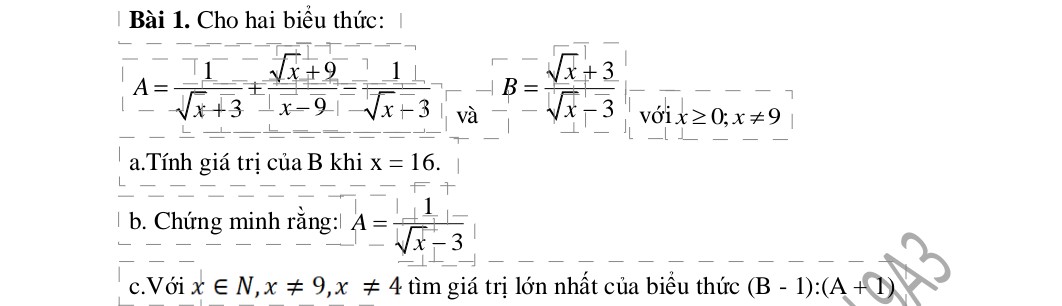
a: Khi x=16 thì \(B=\dfrac{4+3}{4-3}=\dfrac{7}{1}=7\)
b: \(A=\dfrac{1}{\sqrt{x}+3}+\dfrac{\sqrt{x}+9}{x-9}-\dfrac{1}{\sqrt{x}-3}\)
\(=\dfrac{\sqrt{x}-3+\sqrt{x}+9-\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{2\sqrt{x}+6-\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{1}{\sqrt{x}-3}\)

Gọi A,B lần lượt là trung điểm của MP,MN. Gọi O là giao điểm của NA và PB
Ta có: \(MB=BN=\dfrac{MN}{2}\)
\(MA=AP=\dfrac{MP}{2}\)
mà MN=MP
nên MB=BN=MA=AP
Xét ΔBNP và ΔAPN có
BN=AP
\(\widehat{BNP}=\widehat{APN}\)
PN chung
Do đó: ΔBNP=ΔAPN
=>\(\widehat{BPN}=\widehat{ANP}\)
=>\(\widehat{ONP}=\widehat{OPN}\)
=>ON=OP
ΔMNP đều
mà PB là đường trung tuyến
nên PB\(\perp\)MN tại B
=>OB\(\perp\)MN tại B
Xét ΔOMN có
OB là đường cao
OB là đường trung tuyến
Do đó: ΔOMN cân tại O
=>OM=ON
mà ON=OP
nên OM=ON=OP
=>O là tâm đường tròn ngoại tiếp ΔMNP
Xét ΔMNP đều có PB là đường trung tuyến
nên \(PB=MN\cdot\dfrac{\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)\)
Xét ΔMNP có
PB,NA là các đường trung tuyến
PB cắt NA tại O
Do đó: O là trọng tâm của ΔMNP
=>\(OP=\dfrac{2}{3}\cdot PB=\dfrac{2}{3}\cdot5\sqrt{3}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)
=>Bán kính là \(\dfrac{10\sqrt{3}}{3}\left(cm\right)\)
Ta có: \(A=2\sqrt{12}-\sqrt{48}+3\sqrt{27}-\sqrt{108}\)
\(=2\cdot2\sqrt{3}-4\sqrt{3}+3\cdot3\sqrt{3}-6\sqrt{3}\)
\(=4\sqrt{3}-4\sqrt{3}+9\sqrt{3}-6\sqrt{3}\)
\(=3\sqrt{3}\)
A=4\(\sqrt{3}\)-4\(\sqrt{3}\)+9\(\sqrt{3}\)-6\(\sqrt{3}\)
A= 3\(\sqrt{3}\)