Thu gọn:A=4x^2y(-3xy^2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = 2\(x^2\) - 8\(x\) + 1
A = 2(\(x^2-4x+4\)) - 7
A = 2.\(\left(x-2\right)^2\) - 7
Vì \(\left(x-2\right)^2\) ≥ 0 ∀\(x\)
(\(x-2\))\(^2\) - 7 ≥ - 7 ∀\(x\) dấu = xảy ra khi \(x-2=0\rArr x=2\)
Kết luận giá trị nhỏ nhất của biểu thức A = \(2x^2-8x+1\) là -7 xảy ra khi \(x=2\)

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

het - tet
Thay h = 50, e = 9, t = 5 vào biểu thức het - tet ta có:
50.9.5 - 5.9.5 = 9.5.(50 - 5) = 9.5.45 = 45.45 = 2025



Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!


x : 2 = y : (-5)
 Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
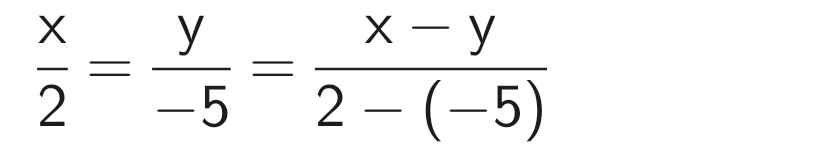

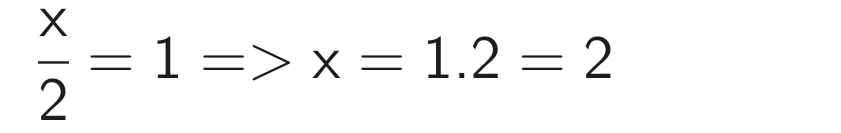
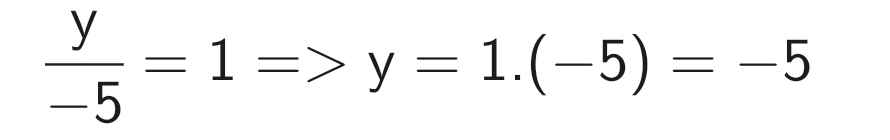
Vậy x = 2; y = -5
Vì 2 và (-5) nguyên tố cùng nhau nên ước chung của 2 và (-5) chỉ có thể là 1 hoặc -1
TH1: (2,-5) = 1
\(\rArr\) x : 2 = 1 \(\rArr\) x=2
y : (-5) = 1 \(\rArr\) y=(-5)
THỬ: 2 + (-5) = 7 (t/mãn)
TH2: (2,-5) = -1
\(\rArr\) x : 2 = -1 \(\rArr\) x=-2
y : (-5) = -1 \(\rArr\) y=5
THỬ: (-2) + 5 = 3 (không thoả mãn)
Vậy x=-2 và y=5
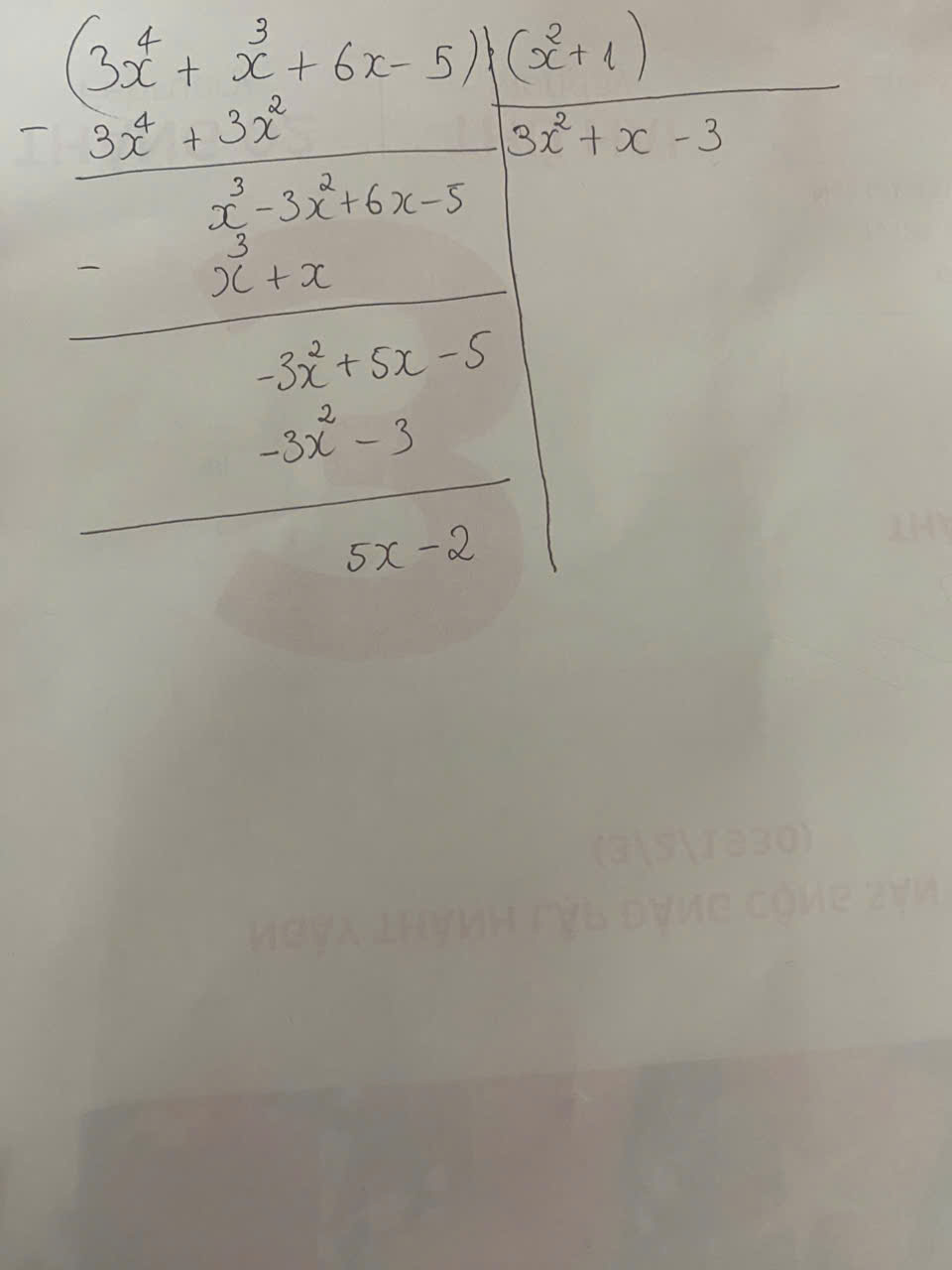

\(A=4x^2y\cdot\left(-3xy^2\right)\)
\(=4\cdot\left(-3\right)\cdot x^2\cdot x\cdot y\cdot y^2\)
\(=-12x^3y^3\)