Gọi d=ƯCLN(-6n+5;4n-3)

=>\(\left\{{}\begin{matrix}-6n+5⋮d\\4n-3⋮d\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}12n-10⋮d\\12n-9⋮d\end{matrix}\right.\)

=>\(12n-10-12n+9⋮d\)

=>\(-1⋮d\)

=>d=1

=>ƯCLN(-6n+5;4n-3)=1

=>\(\dfrac{-6n+5}{4n-3}\) là phân số tối giản

Bài 8:

\(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}\)

\(=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99}\)

\(=\dfrac{1}{3}-\dfrac{1}{99}=\dfrac{33}{99}-\dfrac{1}{99}=\dfrac{32}{99}\)

Bài 6:

a: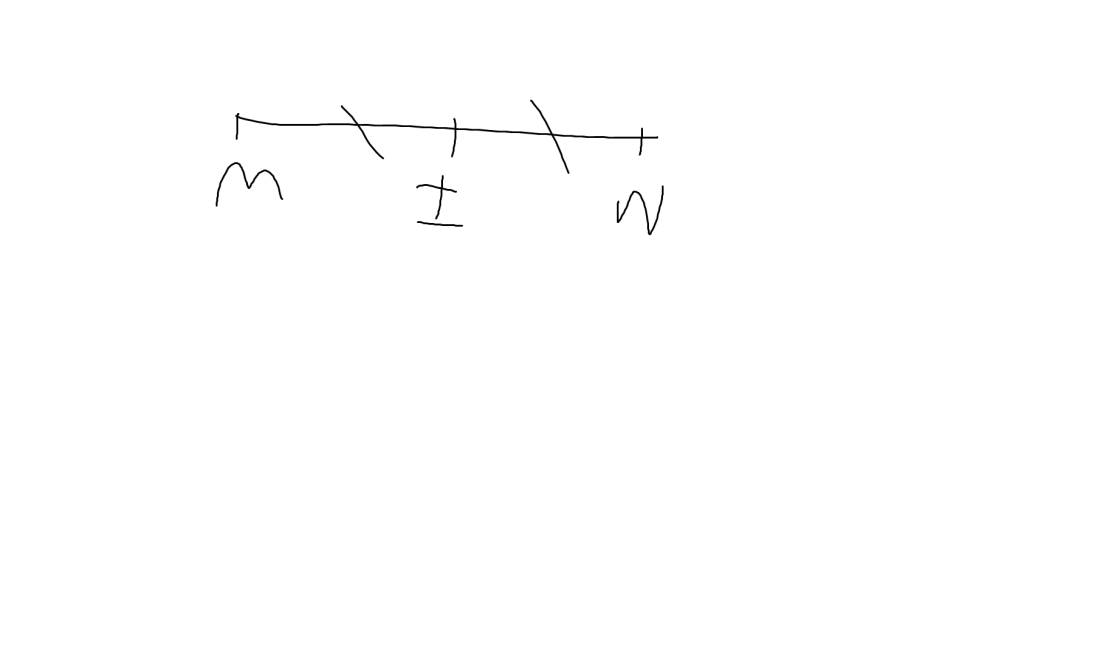 

b: I là trung điểm của MN

=>\(MI=\dfrac{MN}{2}=\dfrac{7}{2}=3,5\left(cm\right)\)

Hhhhh

Ai giải giúp với 

- Thuật toán là một tập hợp các công việc được thực hiện theo một thứ tự nhất định để giải quyết một bài toán trong một số bước đi từ trạng thái đầu vào ban đầu cho đến trạng thái đầu ra kết quả mong muốn.

- Các thành phần chính của thuật toán bao gồm:

+) Thông tin đầu vào.

+) Bước khởi đầu.

+) Các bước thực hiện.

+) Điều kiện dừng thuật toán.

+) Kết quả đầu ra.

Nhanh giúp mình vơi

200 chia 50

ai đúng đc thầy tích nhé!
 

giải theo kiểu lớp 6 được ko ạ?

Căn bậc hai là của lớp 7 ak.

\(x^2-2=0\)

=>\(x^2=2\)

=>\(x=\pm\sqrt{2}\)

a: SỐ tiền lãi anh Duy nhận được sau 1 năm là:

\(200\cdot10^6\cdot5,6\%=11200000\left(đồng\right)\)

Số tiền cả gốc lẫn lãi anh Duy nhận được là:

\(200000000+11200000=211200000\left(đồng\right)\)

b: Số tiền lãi năm thứ hai anh Duy nhận được là:

\(211200000\cdot8\%=16896000\left(đồng\right)\)

Tổng số tiền anh Duy nhận được là:

\(211200000+16896000=228096000\left(đồng\right)\)

Ta có:

\(2020+2021+2022< 2021+2022+2023\)

\(\Rightarrow\dfrac{2020+2021+2022}{2021+2022+2023}< 1\)

\(\Rightarrow Q< 1\)

Lại có: \(2020.2>2021.1\Rightarrow\dfrac{2020}{2021}>\dfrac{1}{2}\)

\(2021.2>2022.1\Rightarrow\dfrac{2021}{2022}>\dfrac{1}{2}\)

\(2022.2>2023.1\Rightarrow\dfrac{2022}{2023}>\dfrac{1}{2}\)

\(\Rightarrow\dfrac{2020}{2021}+\dfrac{2021}{2022}+\dfrac{2022}{2023}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=\dfrac{3}{2}\)

\(\Rightarrow P>\dfrac{3}{2}>1\)

\(\Rightarrow P>Q\)

^{\(\dfrac{2020}{2021}\) > \(\dfrac{2020}{2021+2022+2023}\)}

^{\(\dfrac{2021}{2022}\) > \(\dfrac{2021}{2021+2022+2023}\)}

^{\(\dfrac{2022}{2023}\) > \(\dfrac{2022}{2021+2022+2023}\)}

^{Cộng vế với vế ta có: P = \(\dfrac{2020}{2021}\) + \(\dfrac{2021}{2022}\) + \(\dfrac{2022}{2023}\) > \(\dfrac{2020+2021+2022}{2021+2022+2023}\) = Q}

Ta có: \(6xy+4x+15y+18=0\\ \Leftrightarrow\left(6xy+15y\right)+\left(4x+18\right)=0\\ \Leftrightarrow3y\left(2x+5\right)+2\left(2x+6\right)=0\Leftrightarrow3y\left(2x+5\right)+2\left(2x+5\right)+2=0\\ \Leftrightarrow\left(2x+5\right)\left(3y+2\right)=-2\)

Vì \(x,y\inℤ\) nên \(2x+5\inℤ;3y+2\inℤ\) 

\(\Rightarrow\left(2x+5;3y+2\right)\inƯ\left(-2\right)\\\Rightarrow\left(2x+5;3y+2\right)\in \left\{\pm1;\pm2\right\}\)

Ta có bảng sau:

\(\Rightarrow\left(x;y\right)\in\left\{\left(\dfrac{8}{11};-\dfrac{1}{11}\right);\left(\dfrac{1}{11};\dfrac{4}{11}\right);\left(-\dfrac{8}{11};\dfrac{1}{11}\right);\left(-\dfrac{1}{11};-\dfrac{4}{11}\right)\right\}\)(Loại)

Vậy không có nghiệm \(x,y\inℤ\)