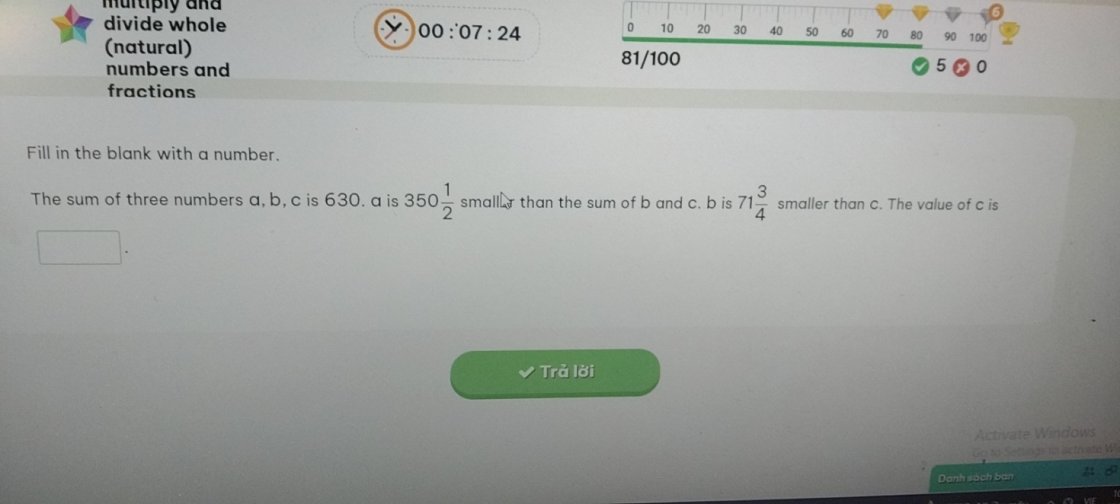
Hãy trả lời mà mình ra đề nhé. Giúp mình nha. Ai thắng thì thưởng 1 tick ( mình giữ lời hứa đó ), ai thua thì đừng lo nha. Sức của ai thì làm nấy. Người chưa trả lời thì vào ngày mai nhé.
TOÁN LỚP 5
Năm học : 2023 - 2024 . Thời gian : 45 phút ( không kể thời gian khi ra đề )
I. Phần trắc nghiệm
Câu 1 : Hãy khoanh trước câu trả lời đúng:
176234 + 341257 + 21 = ?
A. 517440 B. 213458 C. 517512 D. 10912
Câu 2 : Hãy khoanh trước câu trả lời đúng :
12 x 12 + 56 = ?
A. 200 B. 145 C. 149 D. 971
Câu 3 : Hãy khoanh đúng, sai trước câu sau :
a ) 1 giờ + 23 giờ + 67 giờ = 91 giờ Đúng hay Sai ?
b )12 giờ = 60 phút Đúng hay Sai ?
Trả lời :
a) .....
b) .....
II. Phần tự luận
Câu 1 : Đặt tính rồi tính :
109234 + 23 20971 - 132
109 x 25 2312 : 12
Câu 2 : Tính bằng cách thuận tiện nhất :
a) 76513 + 10 x 2 + 230912 + 34 x 2 = .............................
Câu 3 : Tìm x :
12 + x = 23 x : 14 = 1243 + 2314
Câu 4 : Giải bài toán có lời văn :
Nhà bạn Linh có 23 con gà, bạn ấy cần ba gói lương thực thức ăn cho gia đình và con gà mái, gà trống và gà con vào thời tiết lạnh. Bạn Hòa tặng bạn Linh 3 túi lương thực thức ăn để có thể lưu trữ. Mùa đông đã đến, Linh sử dụng lương thực và còn thừa 50 % lượng cơm gạo trong lương thực đó. Hỏi Linh còn thừa bao nhiêu lượng cơm gạo vào ngày thứ hai ?
Câu 5 : Hãy điền vào chỗ trống:
23 > x < 12 .
Chúc các bạn làm tốt nhé.

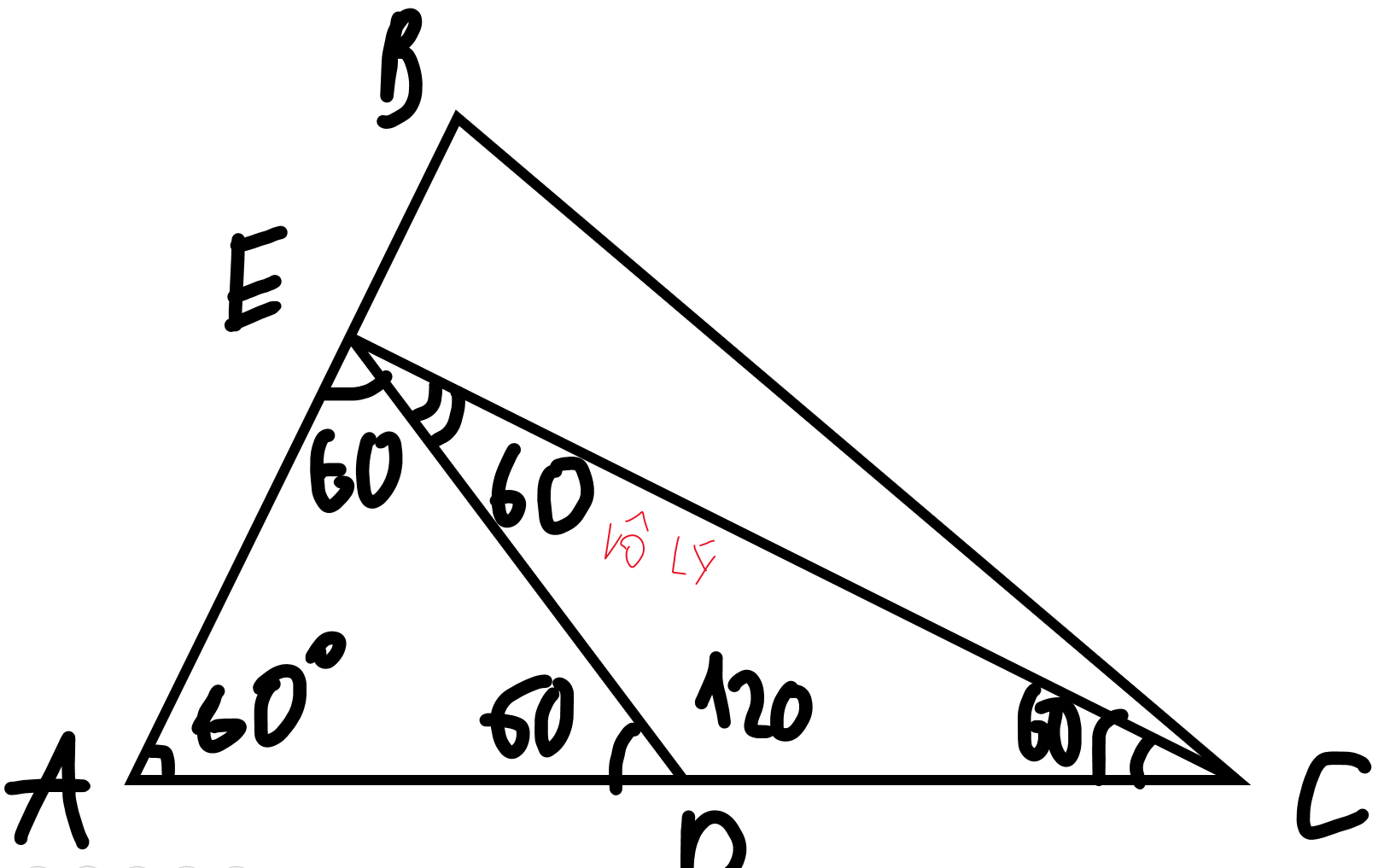
a) Ta có MR//AP nên tứ giác APMR là hình thang.
Lại có MP//BQ nên \(\widehat{MPA}=\widehat{CBA}=\widehat{BAC}=\widehat{RAP}=60^o\)
Hình thang APMR (MR//AP) có \(\widehat{MPA}=\widehat{RAP}\) nên APMR là hình thang cân.
b) Tương tự câu a), ta cũng chứng minh được các tứ giác BPMQ và CQMR là hình thang cân.
Tứ giác APMR là hình thang cân \(\Rightarrow MA=PR\) (2 đường chéo của hình thang cân thì bằng nhau)
Tương tự, suy ra \(MB=PQ,MC=QR\)
\(\Rightarrow MA+MB+MC=PR+PQ+PR=C_{\Delta PQR}\)
Ta có đpcm.
c) \(\Delta PQR\) đều
\(\Leftrightarrow PQ=QR=PR\)
\(\Leftrightarrow MA=MB=MC\) (vì \(MA=PR,MB=PQ,MC=QR\) (cmt))
\(\Leftrightarrow\) M là tâm đường tròn ngoại tiếp tam giác ABC
d) Điểm D là điểm nào đó bạn? Nếu ý bạn là \(\widehat{RMP}=\widehat{PMQ}=\widehat{QMR}\) thì cái này dễ rồi nhé. Dùng tính chất hình thang chứng minh cả 3 góc này bằng 120o là được.
e) Dựng tam giác đều BMN sao cho N và A nằm cùng phía đối với đường thẳng BM.
Khi đó \(BM=BN=MN\), \(\widehat{MBN}=\widehat{ABC}=60^o\)
\(\Rightarrow\widehat{NBM}-\widehat{ABM}=\widehat{ABC}-\widehat{ABM}\)
\(\Rightarrow\widehat{ABN}=\widehat{MBC}\)
Xét tam giác BNA và BMC, ta có:
\(BN=BM\left(cmt\right),\widehat{NBA}=\widehat{MBC}\left(cmt\right),BA=BC\) (tam giác ABC đều)
\(\Rightarrow\Delta BNA=\Delta BMC\left(c.g.c\right)\)
\(\Rightarrow AN=MC\)
Khi đó \(\left\{{}\begin{matrix}MB=MN\\MC=NA\end{matrix}\right.\) nên \(MA,MB,MC\) chính là 3 cạnh của tam giác AMN
Hiển nhiên \(max\left\{MA,MB,MC\right\}\) nhỏ hơn tổng độ dài 2 cạnh còn lại.