tôi là người đẹp trai, siêu siêu đẹp trai!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x\) - \(\dfrac{1}{3}\) = \(\dfrac{1}{2}\)
\(x\) = \(\dfrac{1}{2}\) + \(\dfrac{1}{3}\)
\(x\) = \(\dfrac{5}{6}\)

Trước đây, em vô tình nghe được một câu chuyện cảm động. Sau này, khi nhìn thấy những đóa hoa cúc trắng, em đều không thể không nhớ đến câu chuyện này. Đó chính là Sự tích bông hoa cúc trắng của một nhà văn người Nhật. Đặc biệt, hình ảnh người con gái trong truyện được tác giả xây dựng rất vừa thán phục, vừa cảm động.
Mở đầu câu chuyện, gia cảnh của cô bé đã được tác giả thể hiện rõ qua những câu văn. Nơi cô bé ở thưa người, bố mất sớm và chỉ có hai mẹ con sống nương tựa vào nhau. Gia cảnh không có gì khấm khá, thậm chí còn được coi là khó khăn. Vậy nên, người mẹ mới làm việc chăm chỉ và vất vả qua ngày. Cuối cùng, mẹ kiệt sức nên bị ốm. Qua sự kiện này, tính cách của cô gái nhỏ được thể hiện rõ ràng.
Đầu tiên, có bé là một người con ngoan ngoãn và nghe lời. Tuy tuổi còn nhỏ, cô bé không ham chơi hay nghịch ngợm. Thấy mẹ ốm, cô nghe lời đi tìm thầy thuốc. Tính cách này còn được thể hiện khi gặp thầy thuốc, em dù vội vàng nhưng vẫn vô cùng lễ phép. Chắc hẳn, mẹ rất yêu thương và dạy dỗ cô bé cẩn thận.
Tiếp theo, thứ mà chúng ta cảm nhận được chính là lòng hiếu thảo của người con. Từ việc đi tìm thầy thuốc hay đi lấy hoa chữa bệnh cho mẹ, cô bé đều không ngại khổ. Ngoài trời lạnh giá, tay chân rét lạnh nhưng cô bé vẫn đi một quãng đường rất xa. Ở tầm tuổi nhỏ như vậy, hiếm có ai chịu khó được giá lạnh cả. Nhưng vì tình thương với mẹ, cô bé đã rất dũng cảm.
Cuối cùng, thông qua chi tiết em xé từng cánh hoa nhỏ hơn để mẹ được sống lâu, ta có thể biết đây chính là một cô bé vô cùng thông minh. Vốn dĩ, em có thể cầm bông hoa đó về. Nhưng cô bé có thể nghĩ ra được việc xé từng cánh hoa ra nhỏ hơn. Em thực sự là một cô bé vô cùng thông minh.
Lòng hiếu thảo và thông minh của cô bé trong truyện Sự tích bông hoa cúc trắng là thứ mà không phải ai cũng có được. Thông qua đó, ta cũng cảm nhận được tình cảm gia đình tha thiết, là tình thân không thể chia lìa.

Gọi độ dài quãng đường AB là \(S_{AB}\left(km\right)\).
Lấy mốc thời gian là lúc xe xuất phát \(9h30ph\).
Thời gian xe đi từ A đi trước xe đi từ B là:
\(t_1=9h30ph-9h=30ph=0,5h\)
Quãng đường xe đi từ A đi trước xe đi từ B là:
\(S_1=v_A\cdot t_1=60\cdot0,5=30km\)
Thời gian hai xe cùng đi để gặp được nhau:
\(t=11h30ph-9h30ph=2h\)
Quãng đường xe đi từ A là: \(S_A=v_A\cdot t=60\cdot2=120km\)
Quãng đường xe đi từ B là: \(S_B=v_B\cdot t=70\cdot2=140km\)
Quãng đường AB là: \(S_{AB}=S_A+S_B+S_1=120+140+30=290km\)

Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk; c=dk$. Khi đó:
$\frac{ab}{cd}=\frac{bk.b}{dk.d}=\frac{b^2}{d^2}(1)$
Và:
$\frac{(a-b)^2}{(c-d)^2}=\frac{(bk-b)^2}{(dk-d)^2}=\frac{b^2(k-1)^2}{d^2(k-1)^2}=\frac{b^2}{d^2}(2)$
Từ $(1); (2)$ ta có đpcm.

??????????????????????????????????????????????????????????????

Lời giải:
Trên $AC$ lấy $E$ sao cho $AB=AE$. Xét tam giác $ABD$ và $AED$ có:
$\widehat{BAD}=\widehat{EAD}$ (do $AD$ là tia phân giác $\widehat{A}$)
$AD$ chung
$AB=AE$
$\Rightarrow \triangle ABD=\triangle AED$ (c.g.c)
$\Rightarrow BD=DE(1)$ và $\widehat{ABD}=\widehat{AED}$
Có:
$\widehat{DEC}=180^0-\widehat{AED}=180^0-\widehat{ABD}=\widehat{ECD}+\widehat{BAC}> \widehat{ECD}$
$\Rightarrow DC> DE(2)$
Từ $(1); (2)\Rightarrow DC> DB$

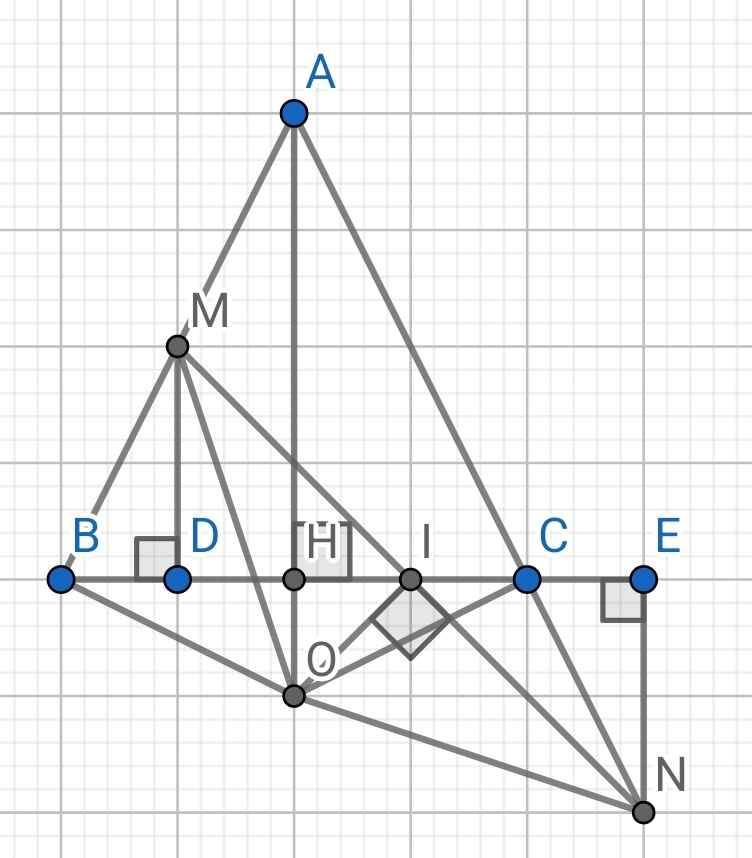 a) ∆ABC cân tại A
a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC

 a) ∆ABC cân tại A
a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC
a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC





Bạn ơi đây là chỗ để các bạn hỏi bài tập bạn đừng đăng linh tinh nhé!
đúng