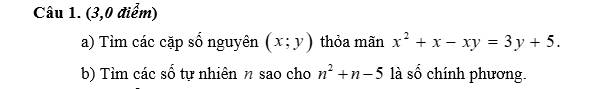Đây là dạng toán nâng cao chuyên đề giải phương trình nghiệm nguyên, cấu trúc thi chuyên, thi học sinh giỏi. Hôm nay Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp bezout như sau.

  \(x^2\) + \(x\) - \(xy\) = 3y + 5

\(x^2\) + \(x\) - 5 = 3y + \(xy\)

\(x^2\) + \(x\) - 5 = y.(3 + \(x\))

y = \(\dfrac{x^2+x-5}{3+x}\)  (1); (đk \(x\) ≠ -3) 

y \(\in\) Z ⇔ \(x^2\) + \(x\) - 5 ⋮ 3 + \(x\) 

Theo bezout ta có:

\(x^2\) + \(x\) - 5 ⋮ 3 + \(x\) 

⇔ (-3)² + (-3) - 5 ⋮ 3 + \(x\)

⇔ 1 ⋮ 3 + \(x\)

3 + \(x\) \(\in\) Ư(1) = {-1; 1}

\(x\) \(\in\) {-4; -2}

Lập bảng ta có:

Theo bảng trên ta có: (\(x;y\)) = (-4; -7); (-2; -3)

Vậy (\(x;y\)) = (-4; -7); (-2; -3)

Bạn thử code này nhé
program RENUM;

var
    S: string;
    frequency: array[0..9] of integer; // Mảng đếm số lần xuất hiện của các số từ 0 đến 9
    maxFreq, maxNum, i, num: integer;

begin
    // Khởi tạo tất cả các phần tử trong mảng đếm về 0
    for i := 0 to 9 do
        frequency[i] := 0;

    // Nhập xâu ký tự S từ bàn phím
    writeln('Nhap vao xau ky tu S: ');
    readln(S);

    // Đếm số lần xuất hiện của các số từ 0 đến 9 trong xâu S
    for i := 1 to length(S) do
    begin
        if (S[i] >= '0') and (S[i] <= '9') then
        begin
            num := ord(S[i]) - ord('0');
            frequency[num] := frequency[num] + 1;
        end;
    end;

    // Tìm số có số lần xuất hiện nhiều nhất và nhỏ nhất
    maxFreq := 0;
    maxNum := 0;
    for i := 0 to 9 do
    begin
        if frequency[i] > maxFreq then
        begin
            maxFreq := frequency[i];
            maxNum := i;
        end;
    end;

    // In ra số xuất hiện nhiều nhất
    if maxFreq > 0 then
        writeln('So xuat hien nhieu nhat la: ', maxNum)
    else
        writeln('Trong xau khong co so nao.');

    readln;
end.

                                Giải

Số hình lập phương được sơn đúng một mặt là:

           (4 - 2) x (4 - 2) x 6 = 24 (hình)

Số hình lập phương có đúng hai mặt được sơn là:

          (4 - 2) x 12 = 24 (hình)

Kết luận: a, có 24 hình lập phương nhỏ được sơn đúng một mặt

                   có 24 hình lập phương nhỏ được sơn đúng hai mặt

a) Ở mỗi mặt, có $4$ hình lập phương nhỏ được sơn một mặt (các hình được gạch sọc).

Ở sáu mặt có: $4.6=24$ (hình).

b) Ở mỗi cạnh, có $2$ hình lập phương được sơn hai mặt (các hình ghi dấu "$x$").

Ở $12$ cạnh có : $2.12=24$ (hình).

Do M là trung điểm của BC (gt)

⇒ BM = BC : 2 = 30 : 2 = 15 (cm)

BD = AB - AD = 10 - 6 = 4 (cm)

Do MD là đường phân giác của ∆AMB (gt)

⇒ AD/BD = AM/BM

⇒ AM = AD . BM : BD

= 6 . 15 : 4

= 22,5 (cm)

A B C M D 6 10 30

Ta có: $AB=AD+DB$

Suy ra $DB=AB-AD=10-6=4$ cm

$AM$ là trung tuyến của $\Delta ABC$ suy ra $M$ là trung điểm của $BC$

Suy ra 𝐵𝑀=𝐶𝑀=12𝐵𝐶=15BM=CM=21​BC=15 cm.

 Xét $\Delta ABM$ có $MD$ là phân giác của góc $AMB$ nên

𝐴𝑀𝐵𝑀=𝐴𝐷𝐷𝐵BMAM​=DBAD​

𝐴𝑀𝐵𝑀=64=32BMAM​=46​=23​

Do đó 𝐴𝑀=32.𝐵𝑀=32.15=22,5AM=23​.BM=23​.15=22,5 (cm).

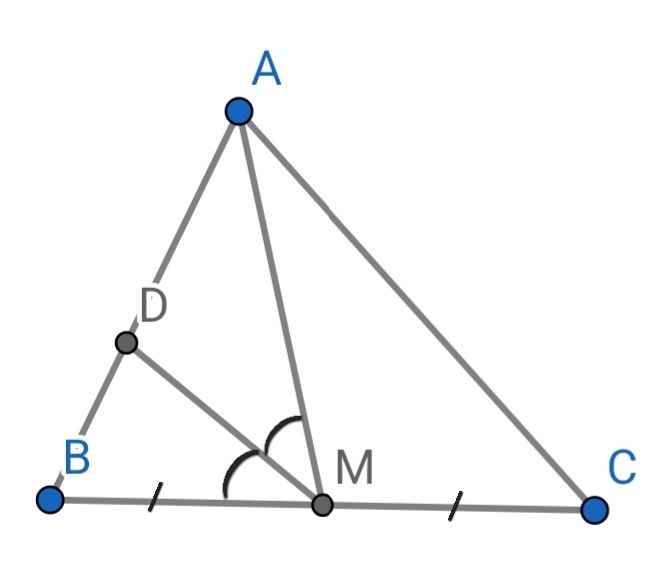
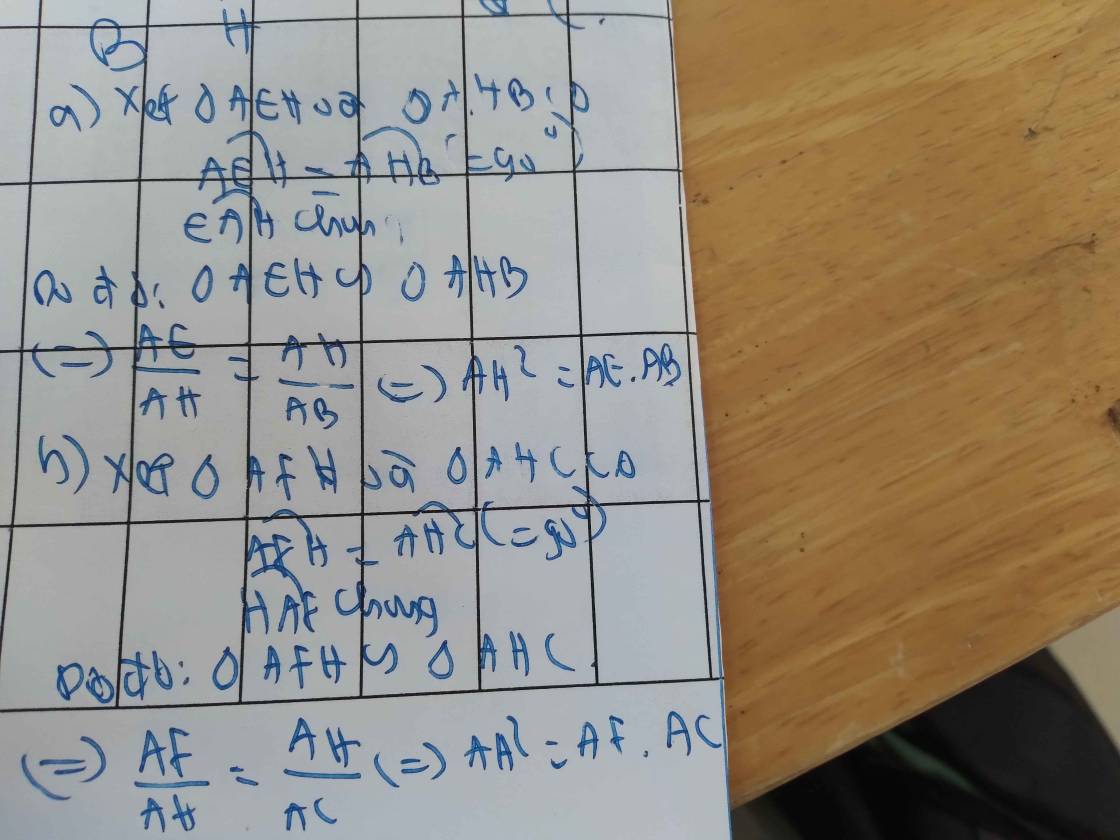
a) Xét hai tam giác vuông: ∆AEH và ∆AHB có:

∠A chung

⇒ ∆AEH ∽ ∆AHB (g-g)

⇒ AH/AB = AE/AH

⇒ AH² = AE.AB

b) Xét hai tam giác vuông: ∆AFH và ∆AHC có:

∠A chung

⇒ ∆AFH ∽ ∆AHC (g-g)

⇒ AH/AC = AF/AH

⇒ AH² = AF.AC

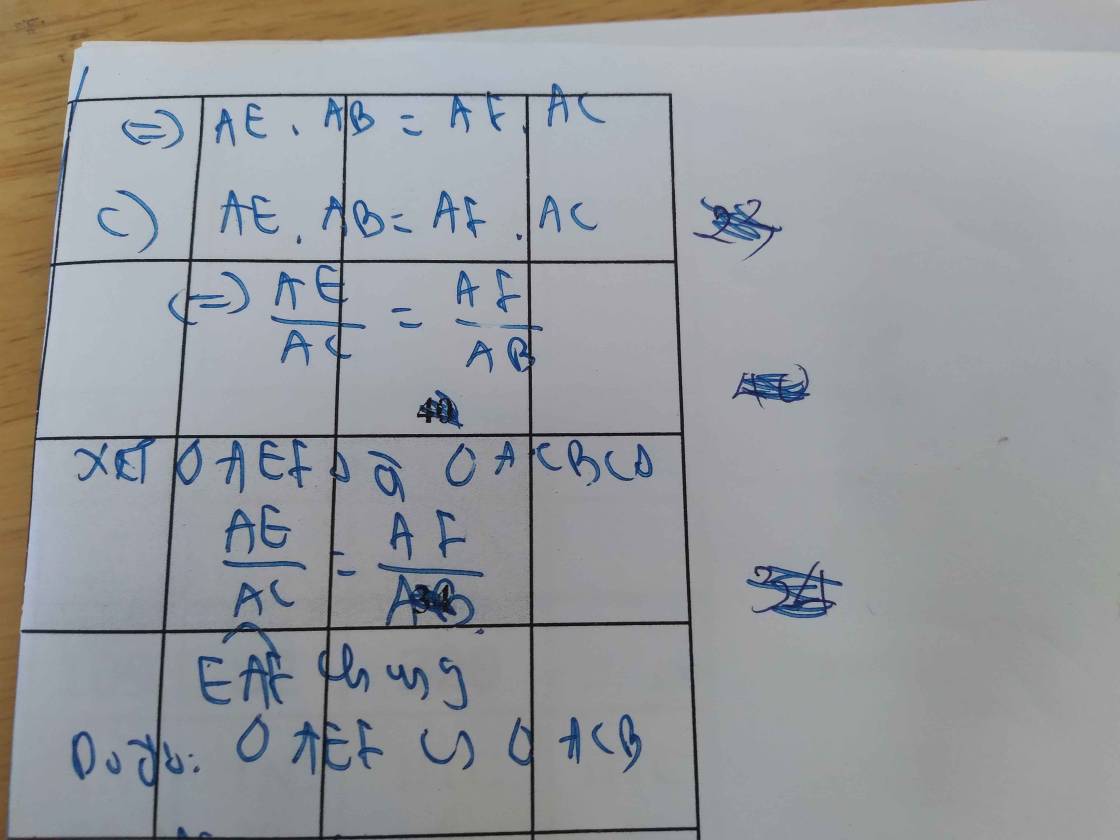
Mà AH² = AE.AB (cmt)

⇒ AE.AB = AF.AC

c) Do AE.AB = AF.AC (cmt)

⇒ AE/AC = AF/AB

Xét ∆AEF và ∆ACB có:

AE/AC = AF/AB (cmt)

∠A chung

⇒ ∆AEF ∽ ∆ACB (c-g-c)

Gọi p và p' lần lượt là chu vi của ∆AEF và ∆ACB

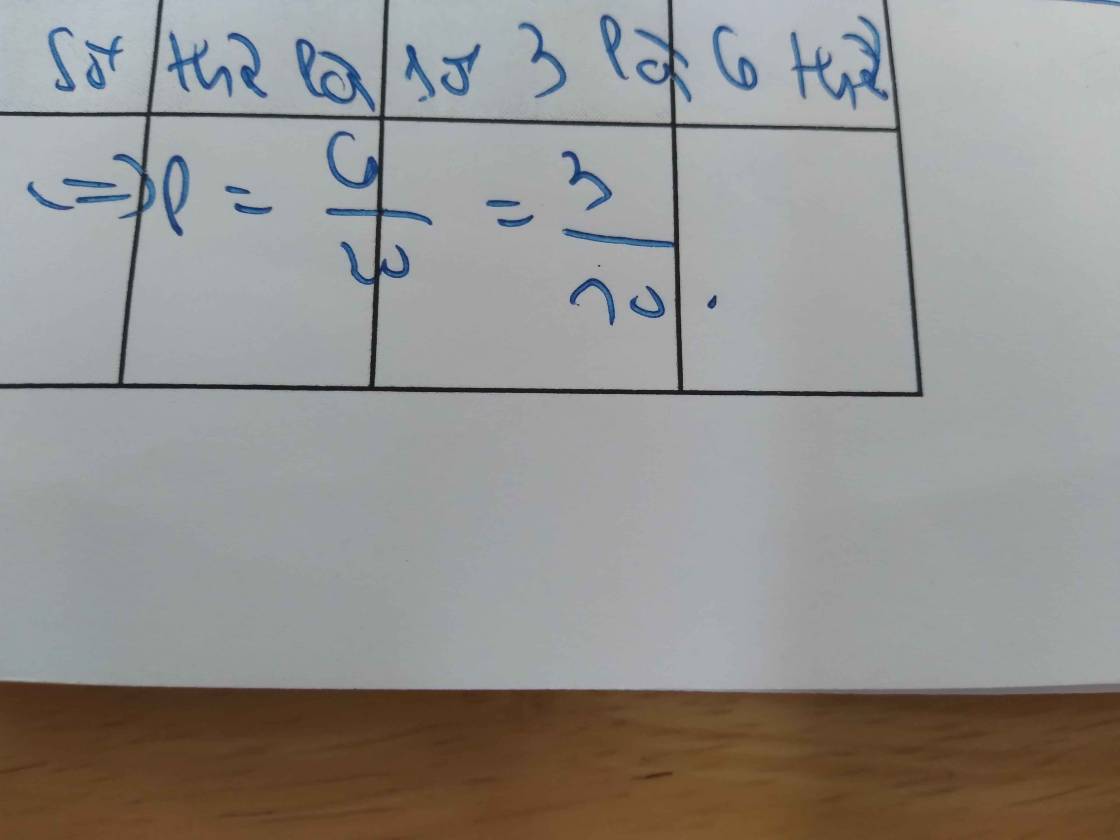
⇒ p/p' = 20/30= 2/3

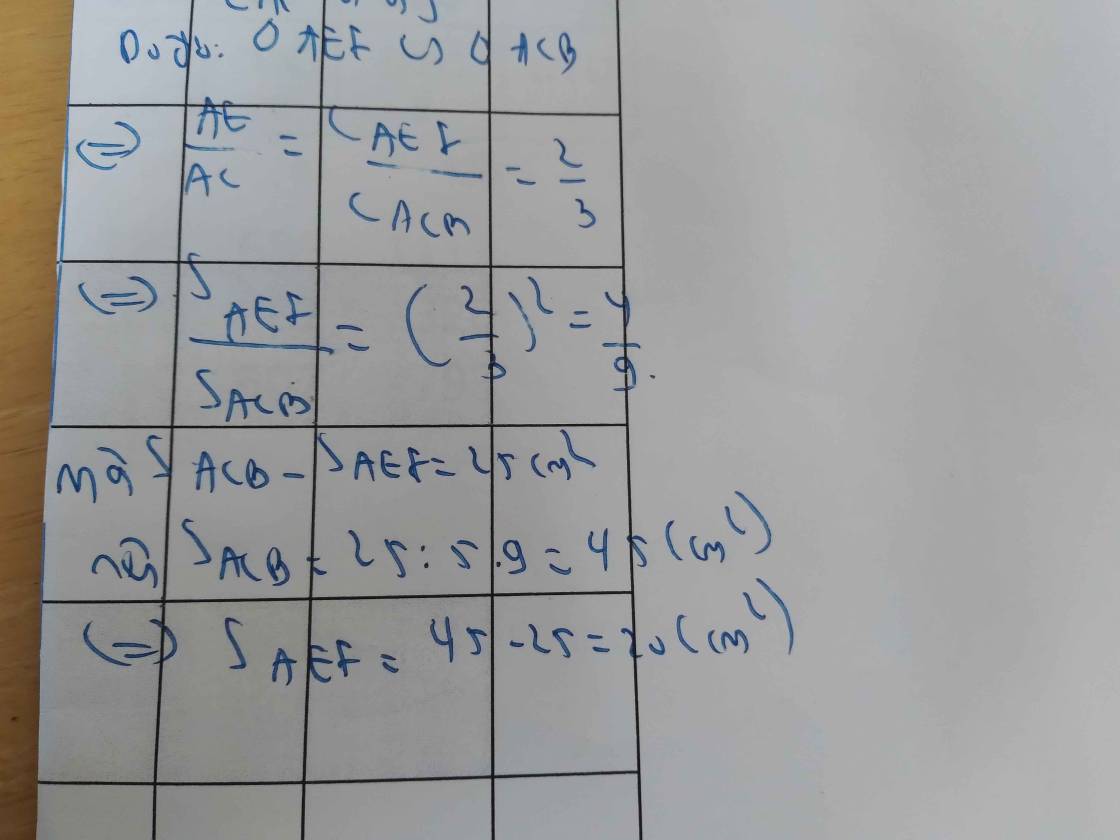
Do ∆AEF ∽ ∆ACB (cmt)

⇒ AE/AC = AF/AB = EF/BC = p/p' = 2/3

Gọi x, y lần lượt là diện tích của ∆AEF và ∆ACB

Do ∆AEF ∽ ∆ACB (cmt)

⇒ x/y = (2/3)² = 4/9

⇒ x/4 = y/9

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

x/4 = y/9 = (y - x)/(9 - 4) = 25/5 = 5

x/4 = 5 ⇒ x = 5.4 = 20 (cm²)

y/9 = 5 ⇒ y = 5.9 = 45 (cm²)

Vậy diện tích ∆AEF là 20 cm², diện tích ∆ACB là 45 cm²

Có 6 khả năng rút được thẻ số 3 nên xác suất của biến cố "Thẻ rút ra là thẻ đánh số 3" là:

P = 6/20 = 3/10

              Giải:

 Đổi 1 giờ 30 phút  = 1,5 giờ

Cứ một giờ ca nô xuôi dòng được: 1 : 1,5  = \(\dfrac{2}{3}\)(quãng sông AB)

Cứ một giờ ca nô ngược dòng được: 1 : 2 = \(\dfrac{1}{2}\) (quãng sông AB)

Cứ một giờ dòng nước chảy được: (\(\dfrac{2}{3}\) - \(\dfrac{1}{2}\)) : 2 = \(\dfrac{1}{12}\)(quãng sông AB)

Quãng sông AB dài là: 3 : \(\dfrac{1}{12}\) = 36 (km)

Vận tốc ca nô khi ngược dòng là: 36 : 2 = 18 (km/h)

Vận tốc riêng của ca nô là: 18 + 3  = 21 (km/h)

Kết luận: Quãng sông AB dài 36 km

               Vận tốc riêng của ca nô là 21 km/h

Gọi x (km/h) là vận tốc riêng của ca nô (x > 3)

Vận tốc đi xuôi dòng từ A đến B: x + 3 (km/h)

1 giờ 30 phút = 1,5 giờ

Quãng đường đi xuôi dòng: (x + 3).1,5 (km)

Vận tốc đi ngược dòng từ B về A: x - 3 (km/h)

Quãng đường đi ngược dòng: (x - 3).2 (km)

Do đi cùng một quãng đường AB nên ta có phương trình:

(x + 3).1,5 = (x - 3).2

1,5x + 4,5 = 2x - 6

2x - 1,5x = 4,5 + 6

0,5x = 10,5

x = 10,5 : 0,5

x = 21 (nhận)

Vậy vận tốc riêng của ca nô là 21 km/h

a) 3x - 4 = 5 + x

3x - 2x = 5 + 4

x = 9

Vậy S = {9}

b) 3(x - 1) - 7 = 5(x + 2)

3x - 3 - 7 = 5x + 10

3x - 10 = 5x + 10

3x - 5x = 10 + 10

-2x = 20

x = 20 : (-2)

x = -10

Vậy S = {-10}

(x - a)/bc + (x - b)/ca + (x - c)/ab = 2/a + 2/b + 2/c

a(x - a) + b(x - b) + c(x - c) = 2bc + 2ac + 2ab

ax - a² + bx - b² + cx - c² = 2bc + 2ac + 2ab

(a + b + c)x = a² + b² + c² + 2bc + 2ac + 2ab

(a + b + c)x = (a + b + c)²

x = (a + b + c)²/(a + b + c)

x = a + b + c

Vậy S = {a + b + c}

Ta có: 𝑥−𝑎𝑏𝑐+𝑥−𝑏𝑐𝑎+𝑥−𝑐𝑎𝑏=2𝑎+2𝑏+2𝑐bcx−a​+cax−b​+abx−c​=a2​+b2​+c2​

(𝑥−𝑎𝑏𝑐−2𝑎)+(𝑥−𝑏𝑐𝑎−2𝑏)+(𝑥−𝑐𝑎𝑏−2𝑐)=0(bcx−a​−a2​)+(cax−b​−b2​)+(abx−c​−c2​)=0

𝑎(𝑥−𝑎)−2𝑏𝑐+𝑏(𝑥−𝑏)−2𝑐𝑎+𝑐(𝑥−𝑐)−2𝑎𝑏𝑎𝑏𝑐=0abca(x−a)−2bc+b(x−b)−2ca+c(x−c)−2ab​=0

Điều kiện xác định: $a,b,c\ne 0$

Khi đó: (𝑎+𝑏+𝑐)𝑥−𝑎2−2𝑏𝑐−𝑏2−2𝑐𝑎−𝑐2−2𝑎𝑏𝑎𝑏𝑐=0abc(a+b+c)x−a2−2bc−b2−2ca−c2−2ab​=0

(𝑎+𝑏+𝑐)𝑥=(𝑎+𝑏+𝑐)2(a+b+c)x=(a+b+c)2 

+ Nếu $a+b+c=0$ thì phương trình có vô số nghiệm.

+ Nếu $a+b+c\ne 0$ thì phương trình có nghiệm duy nhất $x=a+b+c$.