Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a: \(3\in N;3\in Z;3\in Q\)
b: \(10\in N;10\in Z;10\in Q\)
c: \(-\dfrac{3}{7}\in Q\)
d: \(-2\in Z;-2\in Q\)
Bài 2:
\(\dfrac{-3}{5}=\dfrac{-27}{45};\dfrac{-5}{9}=\dfrac{-25}{45};-1\dfrac{2}{3}=\dfrac{-5}{3}=\dfrac{-75}{45};0,5=\dfrac{22,5}{45};\dfrac{10}{9}=\dfrac{50}{45}\)
mà -75<-27<-25<22,5<50
nên \(-1\dfrac{2}{3}< -\dfrac{3}{5}< -\dfrac{5}{9}< \dfrac{1}{2}< \dfrac{10}{9}\)
Bài 1:
a: \(\dfrac{9}{70}=\dfrac{9\cdot3}{70\cdot3}=\dfrac{27}{210};\dfrac{5}{42}=\dfrac{5\cdot5}{42\cdot5}=\dfrac{25}{210}\)
mà 27>25
nên \(\dfrac{9}{70}>\dfrac{5}{42}\)
b: \(\dfrac{-4}{27}=\dfrac{-4\cdot7}{27\cdot7}=\dfrac{-28}{189};\dfrac{10}{-63}=\dfrac{-10}{63}=\dfrac{-10\cdot3}{63\cdot3}=\dfrac{-30}{189}\)
mà -28>-30
nên \(\dfrac{-4}{27}>\dfrac{10}{-63}\)
c: \(\dfrac{999}{556}=1+\dfrac{443}{556};\dfrac{1000}{557}=1+\dfrac{443}{557}\)
mà \(\dfrac{443}{556}>\dfrac{443}{557}\)
nên \(\dfrac{999}{556}>\dfrac{1000}{557}\)
d: \(\dfrac{-2}{15}< 0;\dfrac{-10}{-11}=\dfrac{10}{11}>0\)
Do đó: \(\dfrac{-2}{15}< \dfrac{-10}{-11}\)

1: Xét ΔABC vuông tại A có \(tanC=\dfrac{AB}{AC}\)
=>\(\dfrac{AB}{10}=tan60\)
=>\(AB=10\cdot tan60=10\sqrt{3}\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\)
=>Chọn C
2: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(AB=\sqrt{8^2-6^2}=\sqrt{28}=2\sqrt{7}\left(cm\right)\)
Xét ΔABC vuông tại A có \(tanC=\dfrac{AB}{AC}=\dfrac{2\sqrt{7}}{6}=\dfrac{\sqrt{7}}{3}\cong0,88\)
=>Chọn C
3: \(B=tan20\cdot tan30\cdot tan40\cdot tan50\cdot tan60\cdot tan70\)
\(=\left(tan20\cdot tan70\right)\cdot\left(tan30\cdot tan60\right)\cdot\left(tan40\cdot tan50\right)\)
=1*1*1
=1
=>Chọn B
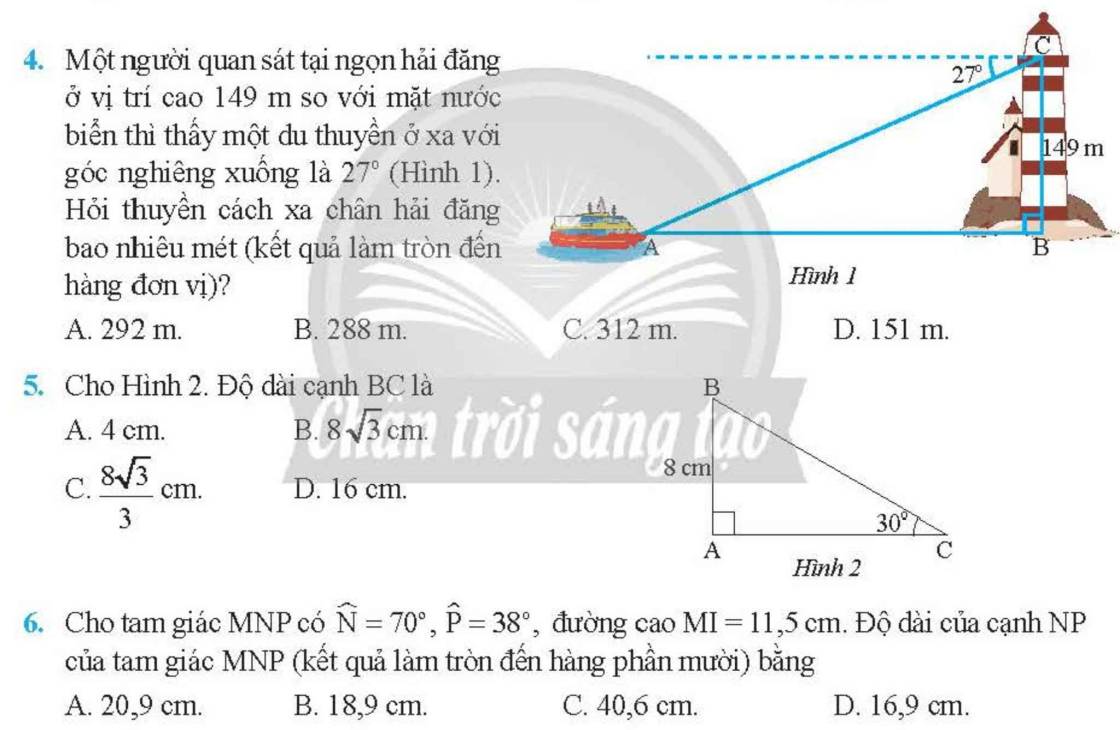
4:
\(\widehat{BAC}=27^0\)
Xét ΔBAC vuông tại B có \(tanBAC=\dfrac{BC}{BA}\)
=>\(BA=\dfrac{149}{tan27}\simeq292\left(m\right)\)
Vậy: Thuyền cách xa chân hải đăng 292m

Ta có:
\(4A+3B-\left(4A+2B\right)=x^2-2x+1-\left(x^2-2x+9\right)\)
\(\Rightarrow B=-8\)
Thay B vào \(4A+2B=x^2-2x+9\) được:
\(4A+2.\left(-8\right)=x^2-2x+9\)
\(\Rightarrow4A=x^2-2x+9+16\)
\(\Rightarrow4A=x^2-2x+25\)
\(\Rightarrow A=\dfrac{x^2-2x+25}{4}\)
Vậy...
\(\left\{{}\begin{matrix}4A+2B=x^2-2x+9\\4A+3B=x^2-2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\4A+3B=x^2-2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\4A+3.\left(-8\right)=x^2-2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\4A-24=x^2-2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\4A=x^2-2x+25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\A=\dfrac{x^2-2x+25}{4}\end{matrix}\right.\)

Tuổi con hiện nay là :
36:6=6(tuổi)
Hiệu tuổi của 2 mẹ con là:
36-6=30(tuổi)
Khi bằng 1/3 tuổi mẹ thì con có số tuổi là:
30:(3-1)x1=15(tuổi)
Tuổi con bằng 1/3 tuổi mẹ sau số năm là :
15-6=9(năm)
Đ/S 9 năm
số tuổi hiện tại của con là: 36 : 6 = 6 (tuổi)
gọi x là số năm cần tìm
tuổi của mẹ sẽ là: 36 + x (tuổi)
tuổi của con sẽ là: 6 + x (tuổi)
theo đề ta có:
\(6+x=\dfrac{1}{3}\cdot\left(36+x\right)\\ 3\cdot\left(6+x\right)=36+x\\ 18+3x=36+x\\ 3x-x=36-18\\ 2x=18\\ x=9\)
vậy sau 9 năm nữa tuổi con bằng 1/3 tuổi mẹ

a: Xét ΔAMC và ΔDMB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔAMC=ΔDMB
b: ΔAMC=ΔDMB
=>\(\widehat{MAC}=\widehat{MDB}\)
=>AC//DB
mà AC\(\perp\)AB
nên BD\(\perp\)BA
c: Xét ΔCAB vuông tại A và ΔDBA vuông tại B có
BA chung
AC=BD
Do đó: ΔCAB=ΔDBA
=>CB=DA
mà \(AM=\dfrac{1}{2}AD\)
nên \(AM=\dfrac{1}{2}CB\)

a: ĐKXĐ: \(x\notin\left\{-1;0;1\right\}\)
\(\dfrac{x+3}{x+1}-\dfrac{x-1}{x}=\dfrac{3x^2+4x+1}{x\left(x-1\right)}\)
=>\(\dfrac{x\left(x+3\right)-\left(x-1\right)\left(x+1\right)}{x\left(x+1\right)}=\dfrac{3x^2+4x+1}{x\left(x-1\right)}\)
=>\(\dfrac{x^2+3x-x^2+1}{\left(x^2+x\right)}=\dfrac{3x^2+4x+1}{x\left(x-1\right)}\)
=>\(\dfrac{\left(3x+1\right)\left(x-1\right)}{x\left(x+1\right)\left(x-1\right)}=\dfrac{\left(3x^2+4x+1\right)\left(x+1\right)}{x\left(x-1\right)\left(x+1\right)}\)
=>\(\left(3x^2+4x+1\right)\left(x+1\right)=\left(3x+1\right)\left(x-1\right)\)
=>\(\left(3x+1\right)\left(x^2+2x+1\right)-\left(3x+1\right)\left(x-1\right)=0\)
=>\(\left(3x+1\right)\left(x^2+2x+1-x+1\right)=0\)
=>\(\left(3x+1\right)\left(x^2+x+2\right)=0\)
mà \(x^2+x+2=\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\forall x\)
nên 3x+1=0
=>\(x=-\dfrac{1}{3}\left(nhận\right)\)
b: ĐKXĐ: \(x\notin\left\{-3;-1\right\}\)
\(\dfrac{x}{2\left(x+3\right)}+\dfrac{x}{2x+2}=\dfrac{-x}{\left(x+1\right)\left(x+3\right)}\)
=>\(\dfrac{x}{2\left(x+3\right)}+\dfrac{x}{2\left(x+1\right)}=\dfrac{-x}{\left(x+1\right)\left(x+3\right)}\)
=>\(\dfrac{x\left(x+1\right)+x\left(x+3\right)}{2\left(x+3\right)\left(x+1\right)}=\dfrac{-2x}{2\left(x+1\right)\left(x+3\right)}\)
=>\(x^2+x+x^2+3x=-2x\)
=>\(2x^2+6x=0\)
=>2x(x+3)=0
=>x(x+3)=0
=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-3\left(nhận\right)\end{matrix}\right.\)
c: ĐKXĐ: \(x\notin\left\{0;\dfrac{3}{2}\right\}\)
\(\dfrac{1}{2x-3}=\dfrac{3}{2x^2-3x}+\dfrac{x}{5}\)
=>\(\dfrac{x-3}{x\left(2x-3\right)}=\dfrac{x}{5}\)
=>\(x^2\left(2x-3\right)=5\left(x-3\right)\)
=>\(2x^3-3x^2-5x+15=0\)
=>\(x\simeq-1,9\left(nhận\right)\)
d: ĐKXĐ: \(x\notin\left\{0;-2\right\}\)
\(\dfrac{x+2}{x}=\dfrac{x^2+5x+4}{x^2+2x}+\dfrac{x}{x+2}\)
=>\(\dfrac{\left(x+2\right)^2}{x\left(x+2\right)}=\dfrac{x^2+5x+4}{x\left(x+2\right)}+\dfrac{x^2}{x\left(x+2\right)}\)
=>\(\left(x+2\right)^2=x^2+5x+4+x^2\)
=>\(2x^2+5x+4-x^2-4x-4=0\)
=>\(x^2+x=0\)
=>x(x+1)=0
=>\(\left[{}\begin{matrix}x=0\left(loại\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)

p là số nguyên tố lớn hơn 3
=>p=3k+1 hoặc p=3k+2
TH1: p=3k+1
\(8p+1=8\left(3k+1\right)+1=24k+8+1=24k+9=3\left(8k+3\right)⋮3\)
=>8p+1 không là số nguyên tố
=>Loại
Do đó: p=3k+2
\(4p+1=4\left(3k+2\right)+1=12k+8+1=12k+9=3\left(4k+3\right)⋮3\)
=>4p+1 là hợp số

1) 152 + 37 + 28 + 238 + 163
= (152 + 138) + (163 + 37) + 28
= 290 + 200 + 28
= 390 + 28
= 418
2) 26 x 54 + 54 x 73
= 54 x (26 + 73)
= 54 x 99
= 54 x (100 - 1)
= 54 x 100 - 54
= 5400 - 54
= 5346
3) 23 x 75 + 25 x 23 +180
= 23 x (75 + 25) + 180
= 23 x 100 + 180
= 2300 + 180
= 2480
4) 12 x 79 + 79 x 172 - 79 x 84
= 79 x (12 + 172 - 84)
= 79 x (184 - 84)
= 79 x 100
= 7900
5) 28 x 47 + 72 x 29 + 28 x 43 + 72 x 61
= 28 x (47 + 43) + 72 x (29 + 61)
= 28 x 90+ 72 x 90
= 90 x (28 + 72)
= 90 x 100
= 9000
6) 24 x 40 + 10 x 8 x 4 + 34 x 80
= 12 x 2 x 40 + 10 x 8 x 4 + 34 x 80
= 12 x 80 + 80 x 4 + 34 x 80
= 80 x (12 + 4 + 34)
= 80 x 50
= 4000
7) (2 + 4 + 6 + ... + 2024) x (125125 x 127 - 127127 x 125)
= (2 + 4 + 6 + ... + 2024) x (125 x 1001 x 127 - 127 x 1001 x 125)
= (2 + 4 + 6 + ... + 2024) x 0
= 0
8) (1 + 3 + 5 + ... + 2021) x (13431 x 131 - 14541 x 121)
= (1 + 3 + 5 + ... + 2021) x (111 x 121 x 131 - 111 x 131 x 121)
= (1 + 3 + 5 + ... + 2021) x 0
= 0
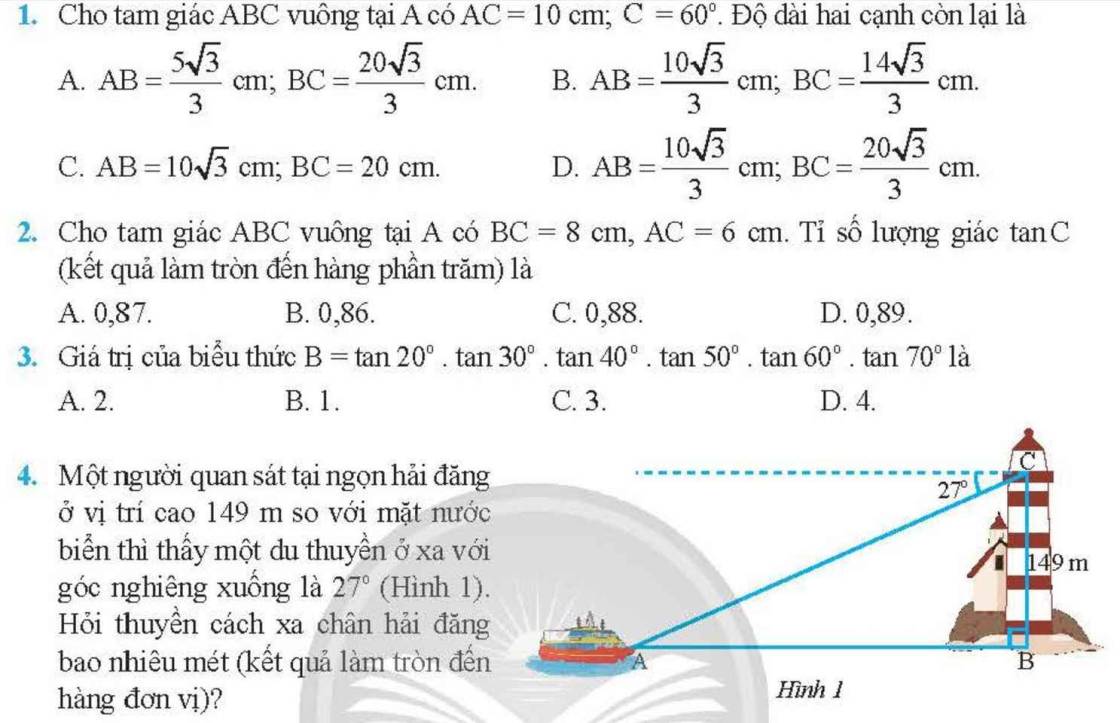


6:
Xét ΔMIN vuông tại I có \(tanN=\dfrac{MI}{NI}\)
=>\(NI=\dfrac{MI}{tanN}=\dfrac{11.5}{tan70}\simeq4,2\left(cm\right)\)
Xét ΔMIP vuông tại I có \(tanP=\dfrac{MI}{IP}\)
=>\(IP=\dfrac{MI}{tanP}=\dfrac{11.5}{tan38}\simeq14,7\left(cm\right)\)
NP=NI+IP=4,2+14,7=18,9(cm)
=>Chọn B
5: Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}\)
=>\(BC=\dfrac{8}{sin30}=16\left(cm\right)\)
=>Chọn D
4:
\(\widehat{BAC}=27^0\)
Xét ΔBAC vuông tại B có \(tanBAC=\dfrac{BC}{BA}\)
=>\(BA=\dfrac{149}{tan27}\simeq292\left(m\right)\)
=>Chọn A