Để chứng minh rằng 2 tia phân giác 2 góc đối đỉnh là 2 tia đối nhau, chúng ta cần sử dụng một số khái niệm và định lý trong hình học. Dưới đây là cách chứng minh:

Giả sử chúng ta có hai tia AB và AC, và chúng phân giác hai góc đối đỉnh, tức là góc BAC và góc CAD. Chúng ta cần chứng minh rằng hai tia AB và AC là hai tia đối nhau.

Để chứng minh điều này, ta sẽ sử dụng Định lý Tia Phân Giác (Bisector Theorem) và Định lý Tia Tiếp Tuyến (Alternate Segment Theorem) như sau:

Bước 1: Vẽ đường thẳng đi qua điểm A và song song với tia BC (đường thẳng đó gọi là đường thẳng d).

Bước 2: Do AB là tia phân giác góc BAC, nên theo Định lý Tia Phân Giác, ta có: AB/BD = AC/CD

Bước 3: Do AC là tia phân giác góc CAD, nên theo Định lý Tia Phân Giác, ta có: AC/CD = AB/BD

Bước 4: Từ Bước 2 và Bước 3, ta có: AB/BD = AC/CD = AB/BD Bước 5: Từ Bước 4, ta suy ra AB = AC.

Vậy, chúng ta đã chứng minh rằng hai tia AB và AC là hai tia đối nhau. Hy vọng cách chứng minh trên giúp bạn hiểu và giải đúng bài tập.

Để chứng minh rằng 2 tia phân giác 2 góc đối đỉnh là 2 tia đối nhau, chúng ta cần sử dụng một số khái niệm và định lý trong hình học. Dưới đây là cách chứng minh:

Giả sử chúng ta có hai tia AB và AC, và chúng phân giác hai góc đối đỉnh, tức là góc BAC và góc CAD. Chúng ta cần chứng minh rằng hai tia AB và AC là hai tia đối nhau.

Để chứng minh điều này, ta sẽ sử dụng Định lý Tia Phân Giác (Bisector Theorem) và Định lý Tia Tiếp Tuyến (Alternate Segment Theorem) như sau:

Bước 1: Vẽ đường thẳng đi qua điểm A và song song với tia BC (đường thẳng đó gọi là đường thẳng d).

Bước 2: Do AB là tia phân giác góc BAC, nên theo Định lý Tia Phân Giác, ta có: AB/BD = AC/CD

Bước 3: Do AC là tia phân giác góc CAD, nên theo Định lý Tia Phân Giác, ta có: AC/CD = AB/BD

Bước 4: Từ Bước 2 và Bước 3, ta có: AB/BD = AC/CD = AB/BD Bước 5: Từ Bước 4, ta suy ra AB = AC.

Vậy, chúng ta đã chứng minh rằng hai tia AB và AC là hai tia đối nhau. Hy vọng cách chứng minh trên giúp bạn hiểu và giải đúng bài tập.

\(x^2-18x+90=x^2-2.x.9+9^2+9=\left(x-9\right)^2+9\\ Vậy:\left(x-9\right)^2+9\ge9\forall x\in R\\ Vậy.GTNN.biểu.thức.là:9.khi.x=9\)

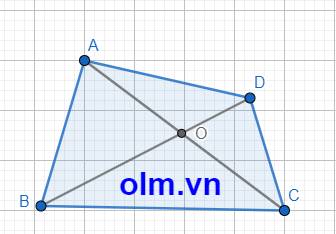
Xét \(\Delta\)AOD ta có: AO + OD > AD (trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)

Xét \(\Delta\) OCD ta có: BO + OC > BC ( trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)

Cộng vế với vế ta có: AO + OD + BO + OC > AD + BC 

                                  (AO + OC) + ( OD + OB > AD + BC

                                   AC+ BD > AD + BC 

Chứng Minh tương tự ta có: AC + BD > AB + CD 

Cho mình xin phép trình bài theo kiểu lớp 8 ạ!

a) Xét ∆ABC vuông tại A có

  BC=CA²+AB²(theo định lí pythagore)

<=>\(BC=\sqrt{AC^2+AB^2}\)

\(\Rightarrow BC=\sqrt{28^2+21^2}\)

\(\Rightarrow BC=35\)

Do AM là trung tuyến với cạnh BC

nên AM=BC:2

\(\Rightarrow AM=\dfrac{35}{2}\)

Mà G là trọng tâm của ∆ABC nên \(AG=\dfrac{2}{3}AM\Leftrightarrow AG=\dfrac{35}{3}\)

b, c đâu bạn

b,Gọi I là giao điểm của BC và ED

Xét ∆AED và ∆ABC có:

+AB=AD(gt)

+\(\widehat{BAC}=\widehat{DAB}\left(=90^o\right)\)

+AC=AE(gt)

\(\Rightarrow\)∆AED=∆ABC(ch-cgv)

\(\Rightarrow\widehat{EDA}=\widehat{ABC}\) (2 góc tương ứng)

Mà \(\widehat{DEA}+\widehat{EDA}=90^o\)( do ∆ADE vuông tại A)

\(\Rightarrow\widehat{CBA}+\widehat{DEA}=90^o\)

\(\Rightarrow\)∆BIE vuông tại I

\(\Rightarrow DE\perp BC\)

Cô làm rồi em nhé:

https://olm.vn/cau-hoi/giup-em-voiii.8161766187032

Số lớn là:

\(42\div3\times11=154\)

Đáp số: \(154\)

a, -0,2; \(\dfrac{1}{1000}\) 

    -0,2 < 0;   \(\dfrac{1}{1000}\)  > 0

    -0,2 < \(\dfrac{1}{1000}\)

b, \(\dfrac{13}{-35}\)  = \(\dfrac{-13.4}{35.4}\) = \(\dfrac{-52}{140}\);    \(\dfrac{-11}{28}\) = \(\dfrac{-11.5}{28.5}\) = \(\dfrac{-55}{140}\)

     vì \(\dfrac{52}{140}\) < \(\dfrac{55}{140}\)

    ⇒ \(\dfrac{-52}{140}\) > \(\dfrac{-55}{140}\) (khi ta nhân cả hai vế của bất đẳng thức với 1 số âm thì dấu của bất đẳng thức đổi chiều.)

Vậy \(\dfrac{13}{-35}\) > \(\dfrac{-11}{28}\) 

c, \(\dfrac{2022}{-2021}\) < - 1 ; \(\dfrac{-1995}{1996}\) > -1

Vậy \(\dfrac{2022}{-2021}\) <  \(\dfrac{-1995}{1996}\) 

d, \(\dfrac{181818}{-131313}\) = \(\dfrac{-181818:10101}{131313:10101}\) = \(\dfrac{-18}{13}\)

vậy \(\dfrac{-18}{13}\)  = \(\dfrac{181818}{-131313}\)

a,b \(\in\) Z, a \(\ne\) b, b > 0 

So sánh: \(\dfrac{a}{b}\) và \(\dfrac{a+2022}{b+2022}\)

  Có hai trường hợp:

+ Nếu a < b ta có:

\(\dfrac{a}{b}\) = 1 - \(\dfrac{b-a}{b}\) ;      \(\dfrac{a+2022}{b+2022}\) = 1 - \(\dfrac{b-a}{b+2022}\) 

Vì \(\dfrac{b-a}{b}\) > \(\dfrac{b-a}{b+2022}\) 

 Vậy : \(\dfrac{a}{b}\) < \(\dfrac{a+2022}{b+2022}\)

+ Nếu a > b ta có 

 \(\dfrac{a}{b}\) = 1 + \(\dfrac{a-b}{b}\);  \(\dfrac{a}{b}\) = 1 + \(\dfrac{a-b}{b+2022}\)

Vì \(\dfrac{a-b}{b}\) > \(\dfrac{a-b}{b+2022}\) 

Vậy \(\dfrac{a}{b}\) > \(\dfrac{a+2022}{b+2022}\) 

a) \(\dfrac{x}{3}=\dfrac{-10}{6}\)

\(x\times6=-10\times3\)

\(x\times6=-30\)

\(x=-5\)

b) \(\dfrac{-8}{x}=\dfrac{-9}{15}\)

\(x\times-9=15\times-8\)

\(x\times-9=-120\)

\(x=\dfrac{40}{3}\)

c) \(\dfrac{2,7}{0,9}=\dfrac{-8}{x}\)

\(x\times2,7=-8\times0,9\)

\(x\times2,7=-7,2\)

\(x=-\dfrac{8}{3}\)

d) \(\dfrac{4}{9}=\dfrac{x}{12}\)

\(x\times9=12\times4\)

\(x\times9=48\)

\(x=\dfrac{48}{9}\)

\(x=\dfrac{16}{3}\)