\(\dfrac{9}{5}< 2;\dfrac{7}{6}< \dfrac{29}{24};3>\dfrac{17}{18}\)

9/5< 2

Vì 10/5=2 mà 9/5<10/5

7/6<29/24

Quy đồng 7/6 và 29/24 ta được 28/24 và 29/24 mà 28/24<29/24

3>17/18

17/18<1 mà 3 > 1

Chúc cậu học tốt, thấy ok thì cho tớ xin một tim nhé!

Lời giải:

Chiều rộng khu đất: $2016:12=168$ (m) 

Tổng chiều dài và chiều rộng khu đất: $102:2=51$ (m) 

Bản thân chiều rộng khu đất còn lớn hơn cả tổng hai chiều, đề có vấn đề bạn xem lại nhé.

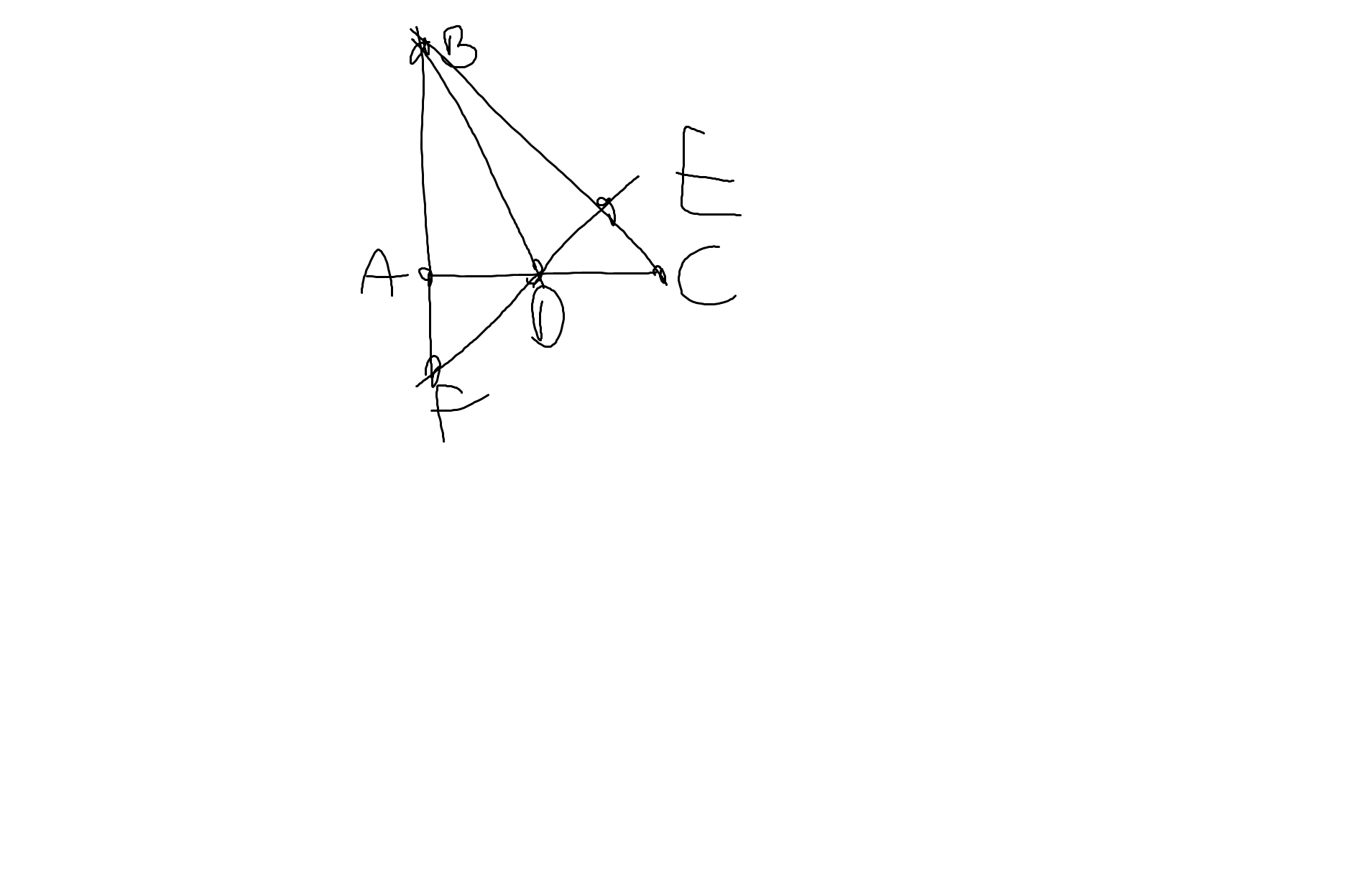
a: Xét ΔBAD và ΔBED có

BA=BE

\(\widehat{ABD}=\widehat{EBD}\)

BD chung

Do đó: ΔBAD=ΔBED
=>DA=DE

b: Ta có: BA=BE

=>B nằm trên đường trung trực của AE(1)

Ta có: DA=DE

=>D nằm trên đường trung trực của AE(2)

Từ (1),(2) suy ra BD là đường trung trực của AE

ΔBAD=ΔBED

=>\(\widehat{BAD}=\widehat{BED}\)

=>\(\widehat{BED}=90^0\)

=>DE\(\perp\)BC tại E

Ta có: ΔDEC vuông tại E

=>DC>DE

mà DE=DA

nên DC>DA

=>AD<DC

c: Ta có: BA+AF=BF

BE+EC=BC

mà BA=BE và BF=BC

nên AF=EC

Xét ΔDAF vuông tại A và ΔDEC vuông tại E có

DA=DE

AF=EC

Do đó: ΔDAF=ΔDEC

=>\(\widehat{ADF}=\widehat{EDC}\)

=>\(\widehat{ADF}+\widehat{ADE}=180^0\)

=>F,D,E thẳng hàng

\(555+123=678\)

555+123=678

Đây là phương trình Pell loại 2 nhé bạn.

\(x^2-5y^2=-1\)    (1)

Xét phương trình liên kết với pt đã cho là \(x^2-5y^2=1\)     (2)

Ta thấy \(\left(9,4\right)\) là nghiệm nguyên dương nhỏ nhất của pt (2)

Xét hệ phương trình: \(\left\{{}\begin{matrix}9=x^2+5y^2\\4=2xy\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^2+5y^2=9\\xy=2\end{matrix}\right.\)   (3). Hệ (3) có nghiệm nguyên dương duy nhất là \(\left(2,1\right)\)

Xét các dãy số nguyên dương \(\left\{x_n\right\},\left\{y_n\right\}\) xác định bởi:

\(\left\{{}\begin{matrix}x_0=2,x_1=38,x_{n+2}=18x_{n+1}-x_n\\y_0=1,y_1=17,y_{n+2}=18y_{n+1}-y_n\end{matrix}\right.\) với \(n\inℕ\)

Khi đó mọi cặp số \(\left(x_n,y_n\right)\) đều là nghiệm của pt đã cho.

VD: Chọn \(n=0\) thì \(\left(x_n,y_n\right)=\left(x_0;y_0\right)=\left(2,1\right)\). Thử lại: \(2^2-5.1^2=-1\) (thỏa mãn) 

 Chọn \(n=1\) thì \(\left(x_n;y_n\right)=\left(x_1;y_1\right)=\left(38;17\right)\). Thử lại:

\(38^2-5.17^2=-1\) (thỏa mãn)

 Dạng tổng quát của pt này là \(x^2-dy^2=-1\)     (1) với \(d\) là số nguyên dương không chính phương. 

 Khi đó xét pt liên kết với (1) là \(x^2-dy^2=1\)    (2). Gọi \(\left(a,b\right)\) là nghiệm nguyên dương nhỏ nhất của (2). 

 Xét hệ pt \(\left\{{}\begin{matrix}a=x^2+dy^2\\b=2xy\end{matrix}\right.\)  (3). Nếu hệ (3) có nghiệm nguyên dương thì (1) cũng có nghiệm nguyên dương. Gọi \(\left(u,v\right)\) là nghiệm nguyên dương duy nhất của (3) thì xét dãy số nguyên dương \(\left\{x_n\right\},\left\{y_n\right\}\) xác định bởi: 

 \(\left\{{}\begin{matrix}x_0=a,x_1=u^3+3duv^2,x_{n+2}=2ax_{n+1}-x_n\\y_0=b,y_1=dv^3+3u^2v,y_{n+2}=2ay_{n+1}-y_n\end{matrix}\right.\) với \(n\inℕ\)

Khi đó \(\left(x_n,y_n\right)\) là tất cả các nghiệm nguyên dương của pt đã cho.

Số chữ số cần dùng để đánh số cho trang có 1 chữ số là:

(9-1+1)x1=9(chữ số)

Số chữ số cần dùng để đánh số cho trang có 2 chữ số là:

(99-10+1)x2=180(chữ số)

SỐ chữ số cần dùng để đánh số cho trang có 3 chữ số là:
(100-100+1)x3=3(chữ số)

Số chữ số cần dùng là:

9+180+3=192(chữ số)

\(2^3.4^3+4^2=\left(2.4\right)^3+4.4\\ =8^3+16\\ =8.8.8+16\\ =512+16=528\)

hoặc:

\(2^3.4^3+4^2\\ =2.2.2.4.4.4+4.4\\ =512+16=528\)

    2³.4³+4^{2
=   2.2.2.4.4.4+4.4
=   512 + 16 = 528
                                                             ~ Chúc bạn họk tốt~}
 

Cả hàng nghìn, trăm, chục và đơn vị đều có 4 cách chọn

Vậy có: 4x4x4x4=256 (số) thỏa mãn yc đề bài

Nếu là số có 4 chữ số khác nhau:

Hàng nghìn có 4 cách chọn

Hàng trăm có 3 cách chọn

Hàng chục có 2 cách chọn

Hàng đơn vị có 1 cách chọn

Vậy có: 4x3x2x1=24 (số) thỏa mãn yc đề bài

Liệt kê các số đó:

1234; 1243; 1324; 1342; 1423; 1432; 2134; 2143; 2314; 2341; 2413; 2431; 3124; 3142; 3214; 3241; 3412; 3421; 4123; 4132; 4213; 4231; 4312; 4321.