chứng minh rằng 2n+1 và 3n+1 là 2 số nguyên tố cùng nhau (với n ko thuộc N)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,-\dfrac{5}{7}+1+\dfrac{30}{-7}\le x\le-\dfrac{1}{6}+\dfrac{1}{3}+\dfrac{5}{6}\\ \dfrac{-5+1.7-30}{7}\le x\le\dfrac{-1+1.2+5}{6}\\ -\dfrac{28}{7}\le x\le\dfrac{6}{6}\\ -4\le x\le1\\ Vậy:x\in\left\{-4;-3;-2;-1;0;1\right\}\)
\(b,\dfrac{-8}{13}+\dfrac{7}{17}+\dfrac{21}{13}\le x\le-\dfrac{9}{14}+3+\dfrac{5}{-14}\\ \left(\dfrac{21}{13}-\dfrac{8}{13}\right)+\dfrac{7}{17}\le x\le\left(-\dfrac{9}{14}-\dfrac{5}{14}\right)+3\\ 1+\dfrac{7}{17}\le x\le-1+3\\ 1\dfrac{7}{17}\le x\le2\\ Vậy:x=2\)

S=1.2+2.3+3.4+...+68.69
⇒ 3S= 1.2.3+2.3.3+3.4.3+...+68.69.3
3S=1.2.3+2.3.(4-1)+3.4.(5-2)+...+68.69.(70-67)
3S=1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+68.69.70-67.68.69
3S=68.69.70
⇒ S=\(\dfrac{68.69.70}{3}\)=328440

a; A = \(\dfrac{3n+1}{2n+3}\) (đk n \(\in\) Z)
A \(\in\) N ⇒ 3n + 1 ⋮ 2n + 3
2.(3n + 1) ⋮ 2n + 3
6n + 2 ⋮ 2n + 3
3(2n + 3) - 7 ⋮ 2n + 3
7 ⋮ 2n + 3
7 = 7 ⇒ Ư(7) = {-7; -1; 1; 7}
Lập bảng ta có:
| 2n + 3 | -7 | -1 | 1 | 7 |
| n | -5 | -2 | -1 | 2 |
| A = \(\dfrac{3n+1}{2n+3}\) | 2 | 5 | -2 (loại) | 1 |
Theo bảng trên ta có: n \(\in\) {-5; -2; 2}
B = \(\dfrac{3n-5}{2n-1}\) (đk n \(\in\) Z)
B \(\in\) N ⇔ 3n - 5 ⋮ 2n - 1
2.(3n - 5) ⋮ 2n - 1
6n - 10 ⋮ 2n - 1
6n - 3 - 7 ⋮ 2n - 1
3.(2n - 1) - 7 ⋮ 2n - 1
7 ⋮ 2n - 1
7 = 7 ⇒ Ư(7) = {-7; - 1; 1; 7}
Lập bảng ta có:
| 2n - 1 | -7 | -1 | 1 | 7 |
| n | -3 | 0 | 1 | 4 |
| B = \(\dfrac{3n-5}{2n-1}\) | 2 | 5 | -2 (loại) | 1 |
Theo bảng trên ta có:
n \(\in\) {-3; 0; 4}

A = 1 - 21 + 22 - 23 +...+298 - 299 + 2100
2A = 2 - 22 + 23 - 24+...+299 - 2100 + 2101
2A + A = 2101 + 1
3A = 2101 + 1
A = \(\dfrac{2^{101}+1}{3}\)

Năm ngoái tuổi của Hùng là:
\(4:\dfrac{2}{5}=10\) (tuổi)
Năm nay tuổi của Hùng là:
\(10+1=11\) (tuổi)
2 năm nữa tuổi của Hùng là:
\(11+2=13\) (tuổi)

a) (x - 3)¹⁰ + (y² - 4)¹⁰ = 0 (1)
Do (x - 3)¹⁰ 0 và (y² - 4)¹⁰ 0 với mọi x, y R
(1) (x - 3)¹⁰ = 0 và (y² - 4)¹⁰ = 0
*) (x - 3)¹⁰ = 0
x - 3 = 0
x = 3
*) (y² - 4)¹⁰ = 0
y² - 4 = 0
y² = 4
y = -2; y = 2
Vậy ta được các cặp (x: y) thỏa mãn:
(3; -2); (3; 2)
b) xy + 5x = 2y + 13
xy + 5x - 2y = 13
(xy + 5x) - 2y = 13
x(y + 5) - 2y - 10 = 13 - 10
x(y + 5) - 2(y + 5) = 3
(x - 2)(y + 5) = 3
*) TH1: x - 2 = -3; y + 5 = -1
+) x - 2 = -3
x = -3 + 2
x = - 1
+) y + 5 = -1
y = -1 - 5
y = -6
*) TH2: x - 2 = -1; y + 5 = -3
+) x - 2 = -1
x = -1 + 2
x = 1
+) y + 5 = -3
y = -3 - 5
y = -8
*) TH3: x - 2 = 1; y + 5 = 3
+) x - 2 = 1
x = 1 + 2
x = 3
+) y + 5 = 3
y = 3 - 5
y = -2
*) TH4: x - 2 = 3; y + 5 = 1
+) x - 2 = 3
x = 3 + 2
x = 5
+) y + 5 = 1
y = 1 - 5
y = -4
Vậy ta tìm được câc cặp giá trị (x; y) thỏa mãn:
(5; -4); (3; -2); (1; -8); (-1; -6)

\(6xy-10x+3y=12\)
\(\Leftrightarrow6xy+3y-10x-5=7\)
\(\Rightarrow3y\left(2x+1\right)-5\left(2x+1\right)=7\)
\(\Leftrightarrow\left(2x+1\right)\left(3y-5\right)=7\)
Ta có bảng:
| 2x+1 | -7 | -1 | 1 | 7 |
| 3y-5 | -1 | -7 | 7 | 1 |
| x | -4 | -1 | 0 | 3 |
| y | 4/3 (loại) | -2/3 (loại) | 4 | 2 |
Vậy \(\left(x;y\right)=\left(0;4\right);\left(3;2\right)\)
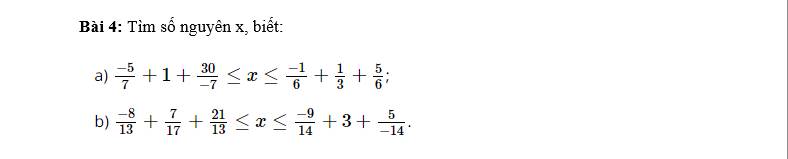

gọi d là UC(2n+1; 3n+1) nên
\(2n+1⋮d\Rightarrow3\left(2n+1\right)=6n+3⋮d\)
\(3n+1⋮d\Rightarrow2\left(3n+1\right)=6n+2⋮d\)
\(\Rightarrow6n+3-\left(6n+2\right)=1⋮d\Rightarrow d=1\)
=> 2n+1 và 3n+1 nguyên tố cùng nhau
Gọi d là ước chung lớn nhất của 2n + 1 và 3n + 1.
Ta có:
Do đó d = ±1
Do đó: ƯCLN (2n + 1; 3n + 1) = 1
Vậy hai số 2n + 1 và 3n + 1 nguyên tố cùng nhau (với n không thuộc N)