Bài 4B:

 \(\widehat{xAB}\) = 180⁰ - 125⁰ = 55⁰

\(\widehat{xAz}\) = \(\widehat{ABY}\) = 125⁰ (vì hai góc đồng vị)

5A. 

\(\widehat{CAB}\) = 180⁰ - 80⁰ = 100⁰

\(\widehat{CAB}\) = \(\widehat{DBZ'}\) = 100⁰ (hai góc đồng vị)

\(\widehat{YBZ'}\) = \(\widehat{ABD}\) = 80⁰

\(x^3:\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}\)

\(\Rightarrow x^3:\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2}\)

\(\Rightarrow x^3=\left(\dfrac{1}{2}\right)^2\cdot\dfrac{1}{2}\)

\(\Rightarrow x^3=\left(\dfrac{1}{2}\right)^3\)

\(\Rightarrow x=\dfrac{1}{2}\)

\(x^3:\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}\Rightarrow x^3=\dfrac{1}{2}.\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}.\left(\dfrac{1}{2}\right)^2=\left(\dfrac{1}{2}\right)^3\)

\(\Rightarrow x=\dfrac{1}{2}\)

Lời giải:

$\sqrt{17}+\sqrt{10}> \sqrt{16}+\sqrt{9}=4+3=7$

\(\sqrt[]{17}+\sqrt[]{10}\Rightarrow\left(\sqrt[]{17}+\sqrt[]{10}\right)^2=17+10+2\sqrt[]{70}=27+2\sqrt[]{70}< 27+2\sqrt[]{100}=47\)

mà \(7^2=49>47\)

\(\Rightarrow\sqrt[]{17}+\sqrt[]{10}< 7\)

Bài 3 :

\(\dfrac{1}{2!}+\dfrac{1}{3!}+\dfrac{1}{4!}+...+\dfrac{1}{2023!}\)

\(\dfrac{1}{2!}=\dfrac{1}{2.1}=1-\dfrac{1}{2}< 1\)

\(\dfrac{1}{3!}=\dfrac{1}{3.2.1}=1-\dfrac{1}{2}-\dfrac{1}{3}< 1\)

\(\dfrac{1}{4!}=\dfrac{1}{4.3.2.1}< \dfrac{1}{3!}< \dfrac{1}{2!}< 1\)

.....

\(\)\(\dfrac{1}{2023!}=\dfrac{1}{2023.2022....2.1}< \dfrac{1}{2022!}< ...< \dfrac{1}{2!}< 1\)

\(\Rightarrow\dfrac{1}{2!}+\dfrac{1}{3!}+\dfrac{1}{4!}+...+\dfrac{1}{2023!}< 1\)

Bạn xem lại đề 2, phần mẫu của N

\(\widehat{MIN}=90^o\) (tính chất 2 đường phân giác cắt nhau tại điểm vuông góc)

A B C M N H E

a/

MN//BC (gt)

\(\Rightarrow\widehat{BMN}=\widehat{BAC}=60^o\) (Góc đông vị)

\(\widehat{BNM}=\widehat{BCA}=60^o\) (góc đồng vị)

\(\widehat{ABC}=60^o\)

\(\Rightarrow\widehat{BMN}=\widehat{BNM}=\widehat{ABC}=60^o\)

=> tg BMN là tg đều => BM = BN

Ta có

AM = AB-BM; CN = BC-BN

Mà AB = BC

=> AM=CN (1)

tg BMN là tg đều nên 3 đường cao cũng đồng thời là 3 đường phân giác; 3 đường trung tuyến => H cũng đồng thời là trọng tâm của tg BMN

Gọi h là đường cao của tg BMN

=> \(HM=HN=\dfrac{2}{3}h\) (2)

\(\widehat{BMH}=\widehat{NMH}=\widehat{MNH}=\widehat{BNH}=\dfrac{60^o}{2}=30^o\)

\(\widehat{AMN}=180^o-\widehat{BMN}=180^o-60^o=120^o\)

\(\widehat{CNM}=180^o-\widehat{BNM}=180^o-60^o=120^o\)

\(\widehat{AMH}=\widehat{AMN}+\widehat{NMH}=120^o+30^o=150^o\)

\(\widehat{CNH}=\widehat{CNM}+\widehat{MNH}=120^o+30^o=150^o\)

\(\Rightarrow\widehat{AMH}=\widehat{CNH}\) (3)

Từ (1) (2) (3) => tg AHM = tg CHN (c.g.c)

b/

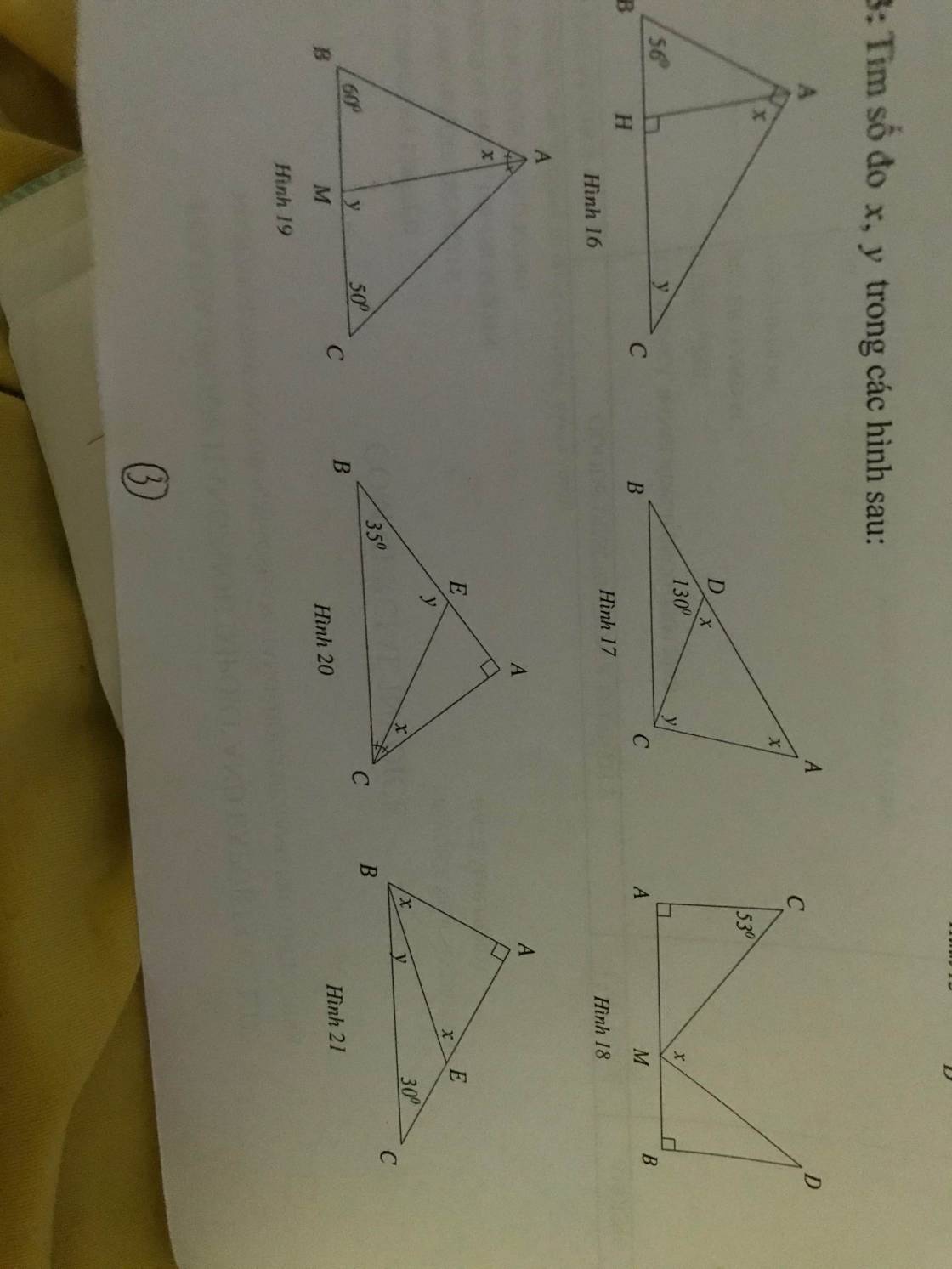
✿ Hình 16:
   △ABC có: ABC+BAC+ \(y\) =180* (đ/lý tổng 3 góc trong 1△)
              T/s 56* + 90* + \(y\) =180* ⇒ \(y\) = 34*
  △△AHC có: \(x\) + \(y\) + AHC=180* (đ/lý tổng 3 góc trong 1△)
             T/s \(x\) + 34*+ 90* =180* ⇒ \(x\) = 56*

Ta đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k\) 

=> \(a=bk\) 

       \(c=dk\) 

Ta có: 

\(\left(\dfrac{a+b}{c+d}\right)^2=\left(\dfrac{bk+b}{dk+d}\right)^2=\left(\dfrac{b\left(k+1\right)}{d\left(k+1\right)}\right)^2=\left(\dfrac{b}{d}\right)^2=\dfrac{b^2}{d^2}\)

\(\dfrac{a^2+b^2}{c^2+d^2}=\dfrac{b^2\times k^2+b^2}{d^2\times k^2+d^2}=\dfrac{b^2\times\left(k^2+1\right)}{d^2\times\left(k^2+1\right)}=\dfrac{b^2}{d^2}\)

=> \(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{a^2+b^2}{c^2+d^2}\) 

=> đpcm

Cảm ơn bạn nha. Mình tick đúng cho bạn rồi đó.

a) Ta có : BD=CE (đề bài)

mà AB=AD+BD; AC=AE+CE; AB=AC (Δ ABC cân tại A)

⇒ AD=AE

⇒ Δ ADE là Δ cân tại A

⇒ Góc ADE = Góc AED

\(\Rightarrow\widehat{DAE}+\widehat{2ADE}=180^O\)

mà \(\widehat{BAC}+\widehat{2ABC}=180^O\) (Δ ABC cân tại A)

\(\Rightarrow\widehat{ADE}=\widehat{ABC}\) ở vị trí đồng vị

Tương tự ta CM \(\widehat{AED}=\widehat{ACB}\) cũng ở vị trí đồng vị

\(\Rightarrow DE//BC\)

b) Xét Δ ABE và Δ ACD ta có :

AB=AC (Δ ABC cân tại A)

Góc A chung

AD=AE (cmt)

⇒ Δ ABE = Δ ACD (cạnh, góc, cạnh)

c) Ta có DE song song BC (cmt)

mà Góc DBC = Góc ECA (Δ ABC cân tại A)

⇒ BDEC là hình thang cân

Xét Δ BID và Δ CIE ta có :

\(\widehat{BDC}=\widehat{DCE}\) (đồng vị)

BD=CE (đề bàI)

BE=CD (BDEC là hình thang cân)

⇒ Δ BID = Δ CIE (cạnh, góc, cạnh)

d) Ta có: AD=AE (cmt)

mà DI=IE (Δ BID = Δ CIE)

⇒ AI là đường trung trực của DE

mà Δ ADE cân tại A (cmt)

⇒ AI là tia phân giác góc BAC

e) Ta có : Δ ABC cân tại A (đề bài)

mà AI là tia phân giác góc BAC (cmt)

⇒ AI là đường cao

⇒ AI vuông góc BC.