\(\left(x+\dfrac{2}{9}\right)^2=\dfrac{4}{81}\\ \left(x+\dfrac{2}{9}\right)^2=\left(\dfrac{2}{9}\right)^2\\ x+\dfrac{2}{9}=\dfrac{2}{9}\\ x=\dfrac{2}{9}-\dfrac{2}{9}\\ x=0\)

Mình bổ sung thêm TH2 nữa. 

\(\left(x+\dfrac{2}{9}\right)^2=\left(-\dfrac{2}{9}\right)^2\\ x+\dfrac{2}{9}=-\dfrac{2}{9}\\ x=-\dfrac{2}{9}-\dfrac{2}{9}\\ x=-\dfrac{4}{9}\)

\(3x-2y=8\\ \left[{}\begin{matrix}3x-2y=8\\3x-2y=8\end{matrix}\right.\\ \left[{}\begin{matrix}3x=2y+8\\2y=3x-8\end{matrix}\right.\\ \left[{}\begin{matrix}\dfrac{3x}{3}=\dfrac{2y+8}{3}\\\dfrac{2y}{2}=\dfrac{3x-8}{2}\end{matrix}\right.\\ \left[{}\begin{matrix}x=\dfrac{2y+8}{3}\\y=\dfrac{3x-8}{2}\end{matrix}\right.\)

Thêm dấu '' \(\Leftrightarrow\) '' mỗi đầu dòng hộ mình nhé.

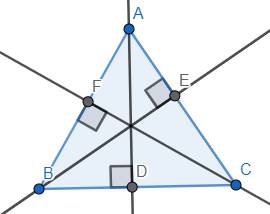
Nhận xét: AD, BE và CF là các đường cao, chúng đồng quy tại một điểm.

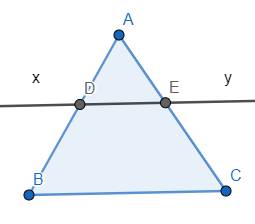
Dễ dàng thấy được \(\widehat{ABC}=\widehat{ADE}\) và \(\widehat{ACB}=\widehat{AED}\) (vì với mỗi cặp thì hai góc của cặp đó là hai góc so le trong)

Vì \(\widehat{ADE}\) và \(\widehat{BDE}\) là hai góc kề bù nên \(\widehat{ADE}+\widehat{BDE}=180^o\)

Mà \(\widehat{ABC}=\widehat{ADE}\) nên \(\widehat{ABC}+\widehat{BDE}=180^o\), suy ra \(\widehat{ABC}\) và \(\widehat{BDE}\) là hai góc bù nhau.

Suy luận tương tự như trên, ta được \(\widehat{ACB}\) và \(\widehat{CED}\) là hai góc bù nhau.

Bạn xem lại đề

\(\left(x-1\right)\left(x-2\right)>0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1< 0\\x-2>0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x< 1\\x>2\end{matrix}\right.\)

Đề yêu cầu gì em nè?

\(x^2+2x< 0\)

\(\Leftrightarrow x\left(x+2\right)< 0\)

\(\Leftrightarrow-2< x< 0\)

Bạn xem lại đề.

Chị mong em xem lại đề bài, ko ổn đâu em

Hình đâu em nhỉ, không có hình thì cô chịu nhé

Để olm.vn  giúp em nhá:

(\(x-5\))²⁰⁰² + (2\(x\) + 1)²⁰⁰⁰ = 0

vì (\(x\) - )²⁰²² ≥ 0 ∀ \(x\) 

    (2\(x\) + 1)²⁰⁰⁰ \(\ge\) 0 ∀ \(x\)

⇒ (\(x\) - 5)²⁰⁰² + (2\(x\) + 1)²⁰⁰⁰ = 0 

   ⇔ \(\left\{{}\begin{matrix}\left(x-5\right)^{2002}=0\\\left(2x+1\right)^{2000}=0\end{matrix}\right.\)

    \(\Rightarrow\) \(\left\{{}\begin{matrix}x-5=0\\2x+1=0\end{matrix}\right.\)

     \(\Rightarrow\) \(\left\{{}\begin{matrix}x=5\\2x=-1\end{matrix}\right.\)

     ⇒   \(\left\{{}\begin{matrix}x=5\\x=-\dfrac{1}{2}\end{matrix}\right.\)

vì - \(\dfrac{1}{2}\) \(\ne\) 5 vậy \(x\in\) \(\varnothing\)

Không thể tìm ''x'' trong bài này.