2:

\(\text{Δ}=\left[-\left(2m-1\right)\right]^2-4\cdot1\cdot\left(m^2-m-2\right)\)

\(=4m^2-4m+1-4m^2+4m+8=9>0\)

=>Phương trình luôn có hai nghiệm phân biệt là:

\(\left[{}\begin{matrix}x=\dfrac{2m-1-\sqrt{9}}{2}=\dfrac{2m-1-3}{2}=m-2\\x=\dfrac{2m-1+3}{2}=\dfrac{2m+2}{2}=m+1\end{matrix}\right.\)

Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m-1\\x_1x_2=\dfrac{c}{a}=m^2-m-2\end{matrix}\right.\)

\(\dfrac{x_1^4+x_1^3+m^2-m-2}{x_1}-\dfrac{x_2^4+x_2^3+m^2-m-2}{x_2}=-7m^2+4m+24\)

=>\(x_1^3+x_1^2+\dfrac{x_1x_2}{x_1}-x_2^3-x_2^2-\dfrac{x_1x_2}{x_2}=-7m^2+4m+24\)

=>\(\left(x_1^3-x_2^3\right)+\left(x_1^2-x_2^2\right)+\left(x_2-x_1\right)=-7m^2+4m+24\)

=>\(\left(x_1-x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)+\left(x_1-x_2\right)\left(x_1+x_2\right)-\left(x_1-x_2\right)=-7m^2+4m+24\)

=>)\(\left(x_1-x_2\right)\left(x_1^2+x_2x_1+x_2^2+x_1+x_2-1\right)=-7m^2+4m+24\)(1)

TH1: \(x_1=m-2;x_2=m+1\)

(1) sẽ tương đương với:

\(\left(m-2-m-1\right)\left[\left(m-2\right)^2+\left(m-2\right)\left(m+1\right)+\left(m+1\right)^2+m-2+m+1-1\right]=-7m^2+4m+24\)

=>\(-3\left[m^2-4m+4+m^2-m-2+m^2+2m+1+2m-2\right]=-7m^2+4m+24\)

=>\(-3\left(3m^2-m+1\right)+7m^2-4m-24=0\)

=>\(-9m^2+3m-3+7m^2-4m-24=0\)

=>\(-2m^2-m-27=0\)

=>\(m\in\varnothing\)

TH2: \(x_1=m+1;x_2=m-2\)

(1) sẽ trở thành:

\(\left(m+1-m+2\right)\left[\left(m+1\right)^2+\left(m+1\right)\left(m-2\right)+\left(m-2\right)^2+2m-1-1\right]=-7m^2+4m+24\)

=>\(3\left(m^2+2m+1+m^2-m-2+m^2-4m+4+2m-2\right)=-7m^2+4m+24\)

=>\(3\left(3m^2-m+1\right)+7m^2-4m-24=0\)

=>\(9m^2-3m+3+7m^2-4m-24=0\)

=>\(16m^2-7m-21=0\)

=>\(m=\dfrac{7\pm\sqrt{1393}}{32}\)

2:

\(\text{Δ}=\left[-\left(2m-1\right)\right]^2-4\cdot1\cdot\left(m^2-m-2\right)\)

\(=4m^2-4m+1-4m^2+4m+8=9>0\)

=>Phương trình luôn có hai nghiệm phân biệt là:

\(\left[{}\begin{matrix}x=\dfrac{2m-1-\sqrt{9}}{2}=\dfrac{2m-1-3}{2}=m-2\\x=\dfrac{2m-1+3}{2}=\dfrac{2m+2}{2}=m+1\end{matrix}\right.\)

Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m-1\\x_1x_2=\dfrac{c}{a}=m^2-m-2\end{matrix}\right.\)

\(\dfrac{x_1^4+x_1^3+m^2-m-2}{x_1}-\dfrac{x_2^4+x_2^3+m^2-m-2}{x_2}=-7m^2+4m+24\)

=>\(x_1^3+x_1^2+\dfrac{x_1x_2}{x_1}-x_2^3-x_2^2-\dfrac{x_1x_2}{x_2}=-7m^2+4m+24\)

=>\(\left(x_1^3-x_2^3\right)+\left(x_1^2-x_2^2\right)+\left(x_2-x_1\right)=-7m^2+4m+24\)

=>\(\left(x_1-x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)+\left(x_1-x_2\right)\left(x_1+x_2\right)-\left(x_1-x_2\right)=-7m^2+4m+24\)

=>)\(\left(x_1-x_2\right)\left(x_1^2+x_2x_1+x_2^2+x_1+x_2-1\right)=-7m^2+4m+24\)(1)

TH1: \(x_1=m-2;x_2=m+1\)

(1) sẽ tương đương với:

\(\left(m-2-m-1\right)\left[\left(m-2\right)^2+\left(m-2\right)\left(m+1\right)+\left(m+1\right)^2+m-2+m+1-1\right]=-7m^2+4m+24\)

=>\(-3\left[m^2-4m+4+m^2-m-2+m^2+2m+1+2m-2\right]=-7m^2+4m+24\)

=>\(-3\left(3m^2-m+1\right)+7m^2-4m-24=0\)

=>\(-9m^2+3m-3+7m^2-4m-24=0\)

=>\(-2m^2-m-27=0\)

=>\(m\in\varnothing\)

TH2: \(x_1=m+1;x_2=m-2\)

(1) sẽ trở thành:

\(\left(m+1-m+2\right)\left[\left(m+1\right)^2+\left(m+1\right)\left(m-2\right)+\left(m-2\right)^2+2m-1-1\right]=-7m^2+4m+24\)

=>\(3\left(m^2+2m+1+m^2-m-2+m^2-4m+4+2m-2\right)=-7m^2+4m+24\)

=>\(3\left(3m^2-m+1\right)+7m^2-4m-24=0\)

=>\(9m^2-3m+3+7m^2-4m-24=0\)

=>\(16m^2-7m-21=0\)

=>\(m=\dfrac{7\pm\sqrt{1393}}{32}\)

Giả sử x+y=0

=>x=-y

\(\left(\sqrt{x^2+3}+x\right)\left(\sqrt{y^2+3}+y\right)\)

\(=\left(\sqrt{\left(-y\right)^2+3}-y\right)\left(\sqrt{y^2+3}+y\right)\)

\(=\left(\sqrt{y^2+3}-y\right)\left(\sqrt{y^2+3}+y\right)\)

\(=y^2+3-y^2=3\)(Đúng với Giả thiết)

=>ĐPCM

minh cam on cau 

Gọi chữ số hàng chục là: a 

Chữ số hàng đơn vị là: b

ĐK: \(1\le a\le9;0\le b\le9\)

Khi đó ta có: \(a-b=5\) (1)

Số đó có dạng: \(\overline{ab}=10a+b\)

Số đó chia cho tổng hai chữ số của nó được thương là 7 và dư 6 nên ta có pt: 

\(\Rightarrow10a+b=7\left(a+b\right)+6\)

\(\Leftrightarrow10a+b=7a+7b+6\)

\(\Leftrightarrow3a-6b=6\Leftrightarrow a-2b=3\left(2\right)\)

Từ (1) và (2) ta có hpt:

\(\left\{{}\begin{matrix}a-b=5\\a-2b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=2\end{matrix}\right.\) (tm)

Vậy số cần tìm là 72 

tham khảo nhé

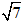
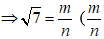
Giả sử  là số hữu tỉ  là phân số tối giản, m; n ∈ Z, m ≠ 0)

Điều này chứng tỏ m2 ⋮ 7 mà 7 là số nguyên tố nên m ⋮ 7

Đặt m = 7k (k ∈ Z), suy ra m2 = (7k)2 = 49k2 (2)

Từ (1) và (2) suy ra: 7n2 = 49k2 ⇒ n2 = 7k2

⇒ n2 ⋮ 7 ⇒ n ⋮ 7 (vì 7 là số nguyên tố)

Do đó cả m và n đều cùng chia hết cho 7, vậy 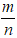 không phải phân số tối giản, mâu thuẫn.

Vậy giả sử sai nên 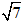 là số vô tỉ (đpcm).

thấy bài mình không

 Ta có \(x+y+xy=3\Leftrightarrow-xy=x+y-3\). Khi đó \(P=\dfrac{3}{x+y}+x+y-3\)

 Đặt \(x+y=t\left(t>0\right)\). Khi đó: \(P=\dfrac{3}{t}+t-3\)

 Lại có  \(xy\le\dfrac{\left(x+y\right)^2}{4}\) \(\Leftrightarrow3=x+y+xy\le\left(x+y\right)+\dfrac{\left(x+y\right)^2}{4}\) \(=t+\dfrac{t^2}{4}\)

 \(\Leftrightarrow t^2+4t\ge12\) \(\Leftrightarrow t\ge2\)

 Khi đó \(P=\dfrac{3}{t}+t-3=\dfrac{3}{t}+\dfrac{3}{4}t+\dfrac{t}{4}-3\) 

\(\ge2\sqrt{\dfrac{3}{t}.\dfrac{3}{4}t}+\dfrac{2}{4}-3\) (chú ý rằng \(t\ge2\)) 

\(=2.\dfrac{3}{2}+\dfrac{1}{2}-3\)

\(=\dfrac{1}{2}\)

Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}t=2\\\dfrac{3}{t}=\dfrac{3}{4}t\end{matrix}\right.\Leftrightarrow t=2\) \(\Leftrightarrow x+y=2\) \(\Rightarrow xy=1\)

\(\Rightarrow x=y=1\)

Vậy \(minP=\dfrac{1}{2}\) khi \(x=y=1\)

Đó là p/s tối giản rồi ạ !

Phân số `-69/68` là phân số tối giản 

Theo mình thì được bạn nhé!

Chắc đc bạn ạ !

Ta có: \(mx+7=6\) (1) (m ≠ 0)

\(\Leftrightarrow mx=-1\)

\(\Leftrightarrow x=\frac{-1}{m}\)

Lại có: \(\frac{x}{2}+m=1\) (2)

\(\Leftrightarrow \frac{x}{2}=1-m\)

\(\Leftrightarrow x=2-2m\)

Để 2 phương trình (1) và (2) có nghiệm bằng nhau thì:

\(\frac{-1}{m}=2-2m\\\Leftrightarrow2m-2-\frac{1}{m}=0\\\Leftrightarrow 2m^2-2m-1=0(\text{vì }m\ne0)\\\Leftrightarrow \left[\begin{array}{} m=\frac{1+\sqrt3}{2}(tmdk)\\ m=\frac{1-\sqrt3}{2}(tmdk) \end{array} \right. \)

$\text{#}Toru$

Ta có pt(1): 

\(mx+7=6\left(m\ne0\right)\)

\(\Leftrightarrow mx=6-7=-1\)

\(\Leftrightarrow x=-\dfrac{1}{m}\)

Pt(2) \(\dfrac{x}{2}+m=1\)

\(\Leftrightarrow\dfrac{x}{2}=1-m\)

\(\Leftrightarrow x=2\left(1-m\right)=2-2m\)

Vì 2 phương trình có nghiệm bằng nhau nên:

\(-\dfrac{1}{m}=2-2m\)

\(\Leftrightarrow-1=m\left(2-2m\right)\)

\(\Leftrightarrow-1=2m-2m^2\)

\(\Leftrightarrow2m^2-2m-1=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1+\sqrt{3}}{2}\\m=\dfrac{1-\sqrt{3}}{2}\end{matrix}\right.\left(tm\right)\)

Vậy: ...

Ta có pt(1): \(mx+7=6\left(m\ne0\right)\)

\(\Leftrightarrow mx=6-7\)

\(\Leftrightarrow mx=-1\)

\(\Leftrightarrow x=-\dfrac{1}{m}\) 

pt(2): \(\dfrac{x}{2+m}=1\left(m\ne-2\right)\)

\(\Leftrightarrow x=1\cdot\left(2+m\right)=m+2\)

Vì 2 pt có 2 nghiệm bằng nhau nên ta có: 

\(-\dfrac{1}{m}=m+2\)

\(\Leftrightarrow-1=m\left(m+2\right)\)

\(\Leftrightarrow-1=m^2+2m\)

\(\Leftrightarrow m^2+2m+1=0\)

\(\Leftrightarrow\left(m+1\right)^2=0\)

\(\Leftrightarrow m+1=0\)

\(\Leftrightarrow m=-1\left(tm\right)\)

Vậy: ...