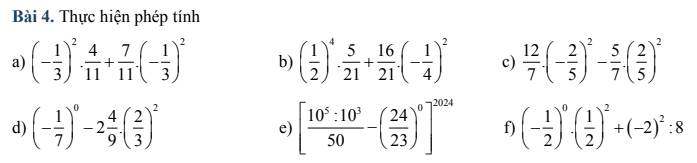
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đề yêu cầu gì thế em?
Tính tổng hay tìm chữ số tận cùng của tổng em nhỉ?

a) \(\left(2x-3\right)^2=16\)
\(\left(2x-3\right)^2=4^2\)
\(2x-3=4\)
\(2x=7\)
\(x=\dfrac{7}{2}=3,5\)
b) \(\left(3x-2\right)^5=-243\)
\(\left(3x-2\right)^5=-3^5\)
\(3x-2=-3\)
\(3x=-1\)
\(3x=-\dfrac{1}{3}\)
c) \(\left(x-7\right)^{x+1}=\left(x-7\right)^{x+11}\)
\(\left(x-7\right)^{x+1}-\left(x-7\right)^{x+11}=0\)
\(\left(x-7\right)^{x+1}\times\left[1-\left(x-7\right)^{10}\right]=0\)
\(\left(x-7\right)^{x+1}=0\) ; \(1-\left(x-7\right)^{10}=0\)
\(x-7=0;\left(x-7\right)^{10}=1\)
\(x=7;\left(x-7=1;x-7=-1\right)\)
\(x=7;x=8;x=6\)
a, (2\(x\) - 3)2 = 16
\(\left[{}\begin{matrix}2x-3=-4\\2x-3=4\end{matrix}\right.\)
\(\left[{}\begin{matrix}2x=-1\\2x=7\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=\dfrac{7}{2}\end{matrix}\right.\)
Vậy \(x\in\){ - \(\dfrac{1}{2}\); \(\dfrac{7}{2}\)}
b, (3\(x\) - 2)5 = -243
( 3\(x\) - 2)5 = (-3)5
3\(x\) - 2 = -3
3 \(x\) = -1
\(x\) = - \(\dfrac{1}{3}\)
Vậy \(x\) = -\(\dfrac{1}{3}\)
c, \(\left(x-7\right)\)\(x+1\) = (\(x-7\))\(x+11\)
(\(x-7\))\(^{x+1}\).( \(\left(x-7\right)^{10}\) - 1 ) = 0
\(\left[{}\begin{matrix}\left(x-7\right)^{x+1}=0\\\left(x-7\right)^{10}=1\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=7\\x-7=-1\\x-7=1\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=7\\x=6\\x=8\end{matrix}\right.\)
Vậy \(x\in\){ 6; 7; 8}

Đề có cho điểm nào cắt điểm nào không ạ hay chỉ có AC//xy ạ?

\(\left(2x+5\right)\left(y-3\right)=22\\ \Rightarrow\left(2x+5\right);\left(y-3\right)\inƯ\left(22\right)=\left\{1;2;11;22\right\}\\ TH1:2x+5=1\Rightarrow x=-2\left(loại\right);\left(y-3\right)=22\Rightarrow y=25\\ TH2:2x+5=2\Rightarrow x=-\dfrac{3}{2}\left(loại\right);\left(y-3\right)=11\Rightarrow y=14\\ TH3:2x+5=11\Rightarrow x=3;\left(y-3\right)=2\Rightarrow y=5\\ TH4:2x+5=22\Rightarrow x=\dfrac{17}{2}\left(loại\right);\left(y-3\right)=1\Rightarrow y=4\\Vậy:\left(x;y\right)=\left(3;5\right)\)

(0,5 )2 .4= ( 0,5 . 2 )2 = 12 = 1
( 0,5)3 . 8 = ( 0,5 . 2 )3 = 13 = 1
(0,5)3 . 32 = ( 0,5 . 2 )3 .22 = 13 .22 = 1.4 = 4
( 0,5)6 . 64 = ( 0,5 . 2 )6 = 16 = 1
5, 0,252 .16 = (0,25.4)2 = 12 = 1
6,(0,25)3 .64 = (0,25 .4 )3 = 13 =1
7,(0,2)2 .25 = ( 0,2 .5 )2 = 12 = 1
8,( 0,2 )3 .125 = ( 0,2 . 5 )3 = 13 = 1

\(a,36-4x^2+20xy-25y^2\\ =36-\left(4x^2-20xy+25y^2\right)\\ =6^2-\left[\left(2x\right)^2-2.2x.5y+\left(5y\right)^2\right]\\ =6^2-\left(2x-5y\right)^2\\ =\left[6-\left(2x-5y\right)\right]\left[6+\left(2x-5y\right)\right]\\ =\left(6-2x+5y\right).\left(6+2x-5y\right)\)
a/
\(=6^2-\left[\left(2x\right)^2-2.2x.5y+\left(5y\right)^2\right]=\)
\(6^2-\left(2x-5y\right)^2=\left[6-\left(2x-5y\right)\right].\left[6+\left(2x-5y\right)\right]\)

\(\left(x-2\right)\left(4x-20\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\4x-20=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\4x=20\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\\ \left(x-5\right)\left(25-5x?\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-5=0\\25-5x=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=5\\5x=25\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=5\\x=5\end{matrix}\right.\\ \left(x-4\right)\left(2x-8\right)\\ \Rightarrow\left[{}\begin{matrix}x-4=0\\2x-8=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=4\\2x=8\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=4\\x=4\end{matrix}\right.\)
a,(x-2)(4x-20)=0
=>x-2=0 hoặc 4x-20=0
=>x=2 hoặc x=5
b,(x-5)(25-5)=0
=>x-5=0 ( vì 25-5 ≠0)
=>x=5
c,(x-4)(2x-8)=0
=>x-4=0 hoặc 2x-8=0
=>x=4

\(A=\dfrac{3}{1^2+2^2}+\dfrac{5}{2^2+3^2}+...+\dfrac{19}{9^2+10^2}\) (sửa \(1^22^2\) thành \(1^2+2^2\))
Ta có : \(\left(1+2\right)^2=1^2+2^2+2.1.2\Rightarrow1^2+2^2< \left(1+2\right)^2\)
\(\Rightarrow1^2+2^2< 3^2=3.3\)
\(\Rightarrow\dfrac{3}{1^2+2^2}< \dfrac{1}{3}< 1\)
Tương tự \(\dfrac{5}{2^2+3^2}< \dfrac{1}{5}< 1\)
\(.....\)
\(\dfrac{9}{9^2+10^2}< \dfrac{1}{19}< 1\)
\(\Rightarrow A=\dfrac{3}{1^2+2^2}+\dfrac{5}{2^2+3^2}+...+\dfrac{19}{9^2+10^2}< 1.9=9< 1\)
\(\Rightarrow dpcm\)

\(a,\left(-\dfrac{1}{3}\right)^2.\dfrac{4}{11}+\dfrac{7}{11}.\left(-\dfrac{1}{3}\right)^2=\left(-\dfrac{1}{3}\right)^2.\left(\dfrac{4}{11}+\dfrac{7}{11}\right)\\ =\dfrac{1}{9}.1=\dfrac{1}{9}\\ b,\left(\dfrac{1}{2}\right)^4.\dfrac{5}{21}+\dfrac{16}{21}.\left(-\dfrac{1}{4}\right)^2\\ =\dfrac{1}{16}.\dfrac{5}{21}+\dfrac{16}{21}.\dfrac{1}{16}\\ =\left(\dfrac{5}{21}+\dfrac{16}{21}\right).\dfrac{1}{16}=1.\dfrac{1}{16}=\dfrac{1}{16}\\ c,\dfrac{12}{7}.\left(-\dfrac{2}{5}\right)^2-\dfrac{5}{7}.\left(\dfrac{2}{5}\right)^2\\ =\left(\dfrac{12}{7}-\dfrac{5}{7}\right).\dfrac{4}{25}\\ =1.\dfrac{4}{25}=\dfrac{4}{25}\)
\(d,\left(-\dfrac{1}{7}\right)^0-2\dfrac{4}{9}.\left(\dfrac{2}{3}\right)^2=1-\dfrac{22}{9}.\dfrac{4}{9}\\ =1-\dfrac{88}{99}=1-\dfrac{8}{9}=\dfrac{1}{9}\\ e,\left[\dfrac{10^5:10^3}{50}-\left(\dfrac{24}{23}\right)^0\right]^{2024}=\left[\dfrac{10^2}{50}-1\right]^{2024}=\left[\dfrac{100}{50}-1\right]^{2024}=\left[2-1\right]^{2024}\\ =1^{2024}=1\\ f,\left(-\dfrac{1}{2}\right)^0.\left(\dfrac{1}{2}\right)^2+\left(-2\right)^2:8=1.\dfrac{1}{4}+-4:8\\ =\dfrac{1}{4}-\dfrac{1}{2}=-\dfrac{1}{4}\)