So sánh phân số \(\dfrac{311}{256}\) và \(\dfrac{199}{203}\)
giúp mik vớiii
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{-49}{211}< \dfrac{13}{1999}\)vì số âm luôn luôn bé hơn số dương.

Ta có : (xy-y^2)+x-y=7
(x-.y).y+(x-y)=7
(x-y).(y+1)=7
Ư(7)={1;7}
Giả sử 1: x-y=1=>x=7
y+1=7=>y=6( tm)
Giả sử 2: x-y=7=>x=7
y+1=1=>y=0
Vậy x= 7 và y=6
x=7 và y=0


Lời giải:
\(E=\frac{\frac{2013}{1}.\frac{2014}{2}.\frac{2015}{3}....\frac{3012}{1000}}{\frac{1001}{1}.\frac{1002}{2}.\frac{1003}{3}....\frac{3012}{2012}}\\ =\frac{2013.2014.2015....3012}{1001.1002.1003....3012}.\frac{1.2.3...2012}{1.2.3..1000}\\ =\frac{1}{1001.1002...2012}.(1001.1002....2012)=1\)

Bài 5:
Muốn làm bài quy đồng mẫu số thì cần tìm BCNN của các mẫu. Với mẫu $a$ và BCNN là $ak$ thì ta nhân cả tử với mẫu với $k$ để quy đồng.
a. \(\frac{1}{4}=\frac{3}{12}; \frac{5}{6}=\frac{10}{12}\)
b. $\frac{-18}{240}=\frac{-18}{240}; \frac{7}{-80}=\frac{-21}{240}$
c. $\frac{-3}{16}=\frac{-9}{48}; \frac{5}{24}=\frac{10}{48}$
d. $\frac{24}{-143}=\frac{-24}{143}; \frac{6}{13}=\frac{-66}{143}$
e. $\frac{-3}{16}=\frac{-9}{48}; \frac{5}{24}=\frac{10}{48}; \frac{-21}{56}=\frac{-3}{8}=\frac{-18}{48}$
f. $\frac{11}{18}=\frac{22}{36}; \frac{-5}{9}=\frac{-20}{36}; \frac{-8}{12}=\frac{-24}{36}$
g.
$\frac{15}{-25}=\frac{-3}{5}=\frac{-9}{15}$
$\frac{-4}{15}=\frac{-4}{15}$
$\frac{1}{3}=\frac{5}{15}$
h.
$\frac{5}{21}=\frac{20}{84}$
$\frac{3}{-28}=\frac{-3}{28}=\frac{-9}{84}$
$\frac{-45}{108}=\frac{-5}{12}=\frac{-35}{84}$

1) \(\left(\dfrac{1}{31}\right)^8=\dfrac{1}{31^8}=\dfrac{1}{\left(31^4\right)^2}=\dfrac{1}{923521^2}\)
\(\left(\dfrac{1}{128}\right)^6=\dfrac{1}{128^6}=\dfrac{1}{\left(128^3\right)^2}=\dfrac{1}{2097152^2}\)
Do \(923521< 2097152\Rightarrow923521^2< 2097152^2\)
\(\Rightarrow\dfrac{1}{923521^2}>\dfrac{1}{2097152^2}\)
\(\Rightarrow\left(\dfrac{1}{31}\right)^8>\left(\dfrac{1}{128}\right)^6\)
2)
Ta có:
\(n+2>n\)
\(\Rightarrow\dfrac{n+2}{n+11}>\dfrac{n}{n+11}\left(1\right)\)
\(n+11< n+13\)
\(\Rightarrow\dfrac{n}{n+11}>\dfrac{n}{n+13}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{n+2}{n+11}>\dfrac{n}{n+13}\)

Xin lỗi chút vì trl ko liên quan:
Nãy h bận chat với bn nên bây h làm chậm nhé!
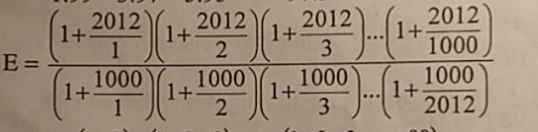

\(\dfrac{311}{256}\) và \(\dfrac{199}{203}\)
Ta dùng cách so sánh 2 phân số với 1:
\(\dfrac{311}{256}>1\) \(;\) \(\dfrac{199}{203}< 1\)
Vậy ta có: \(\dfrac{311}{256}>1>\dfrac{199}{203}\)
Vậy \(\dfrac{311}{256}>\dfrac{199}{203}\)
311/256 > 199/203