a) Ta có \(\widehat{AHK}=\dfrac{sđ\stackrel\frown{AE}+sđ\stackrel\frown{BD}}{2}\) 

và \(\widehat{AKH}=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{AD}}{2}\)

 Mặt khác, do D, E lần lượt là điểm chính giữa của cung AB, AC nên \(sđ\stackrel\frown{AD}=sđ\stackrel\frown{BD};sđ\stackrel\frown{AE}=sđ\stackrel\frown{CE}\). Từ đó \(\Rightarrow\widehat{AHK}=\widehat{AKH}\) hay tam giác AHK cân tại A (đpcm).

 b) Hiển nhiên I là tâm đường tròn nội tiếp tam giác ABC \(\Rightarrow\) AI là tia phân giác của \(\widehat{BAC}\) (hay chính là \(\widehat{HAK}\)). Mà theo câu a), tam giác AHK cân tại A nên AI đồng thời là đường cao của tam giác AHK \(\Rightarrow AI\perp HK\) hay \(AI\perp DE\) (đpcm)

 c) Ta có \(\widehat{CIE}=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{BD}}{2}\)

\(=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{AD}}{2}\) \(=\widehat{CKE}\)  nên tứ giác CEKI nội tiếp 

 \(\Rightarrow\widehat{HKI}=\widehat{DCE}\) \(=\dfrac{sđ\stackrel\frown{DE}}{2}\) 

\(=\dfrac{sđ\stackrel\frown{DA}+sđ\stackrel\frown{AE}}{2}\)  \(=\dfrac{sđ\stackrel\frown{BD}+sđ\stackrel\frown{AE}}{2}\)  \(=\widehat{AHK}\)

Từ đó dễ dàng suy ra KI//AH hay KI//AB (đpcm)

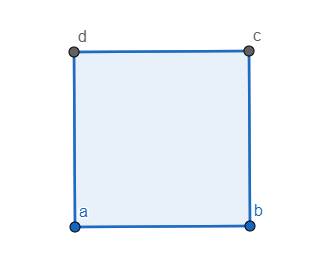
 Xét 1 mặt bất kì của khối lập phương như hình vẽ và gọi 4 số ở đỉnh là a, b, c, d. Khi đó do \(a+b+c,b+c+d,c+d+a,d+a+b\ge10\) nên \(3\left(a+b+c+d\right)\ge40\) \(\Rightarrow a+b+c+d\ge14\)

 Làm tương tự cho 4 mặt còn lại, ta đều được tổng của 4 số trên mỗi mặt đều không nhỏ hơn 14.

 Nhưng trong một mặt, sẽ có mặt có chứa đỉnh mang số 8. Khi đó 3 đỉnh còn lại bắt buộc là 1, 2, 3, mà \(1+2+3< 10\), vô lí. Lập luận tương tự cho trường hợp GTNN là 15, 16, 17. Nếu GTNN là 18, ta chỉ ra 1 trường hợp dấu "=" xảy ra:

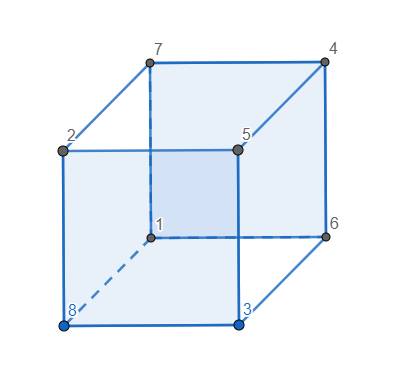
Vậy GTNN của 4 số trong cùng 1 mặt là 18.

a) \(S=5+5^2+...+5^{2006}\)

\(5S=5^2+5^3+...+5^{2007}\)

\(5S-S=5^2+5^3+5^4+...+5^{2007}-5-5^2-5^3-...-5^{2006}\)

\(4S=5^{2007}-5\)

\(S=\dfrac{5^{2007}-5}{4}\)

b) \(S=5+5^2+5^3+...+5^{2006}\)

\(S=\left(5+5^4\right)+\left(5^2+5^5\right)+...+\left(5^{2003}+5^{2006}\right)\)

\(S=5\cdot\left(1+5^3\right)+5^2\cdot\left(1+5^3\right)+...+5^{2003}\cdot\left(1+5^3\right)\)

\(S=\left(1+5^3\right)\cdot\left(5+5^2+...+5^{2003}\right)\)

\(S=126\cdot\left(5+5^2+...+5^{2003}\right)\) ⋮ 126 

2.25 nhân 1

Căn bậc của 2,25 là 1,5 

=>  1,5 x 1,5 = 2,25

Gọi sau ít nhất số ngày ba bạn lại cùng trực là a(ngày,a thuộc N*)

Theo bài ra ta có:

a chia hết cho 5

a chia hết cho 10

a chia hết cho 8

=>a thuộc BCNN(5,10,8)

Ta có:

5=5

10=2x5

8=2^3

=>BCNN(5,10,8)=2^3X5=40

(tiếp câu trên)

=>a=40

Vậy sau 40  ngày ba bạn lại cùng trực nhật

                              Bầu trời chưa đen tối mực

                 Cảnh quang ấm áp , tình thương ngọt bùi 

                              Mặt trời ngáp ngắn ngáp dài

               Hoàng hôn bóng mát, bước chân em về

               Lấy chồng Xa xứ 

 Hoàng hôn đã nhuộm bầu không,

Lục bình tím ngắt mênh mông nỗi buồn.

  Chiều nao ra đứng triền sông,

Ngóng về xứ mẹ hoen tròng lệ rơi!

     Tác giả Thương Hoài olm 

Ta có:

\(A=1+2+2^2+...+2^{2002}\)

\(2A=2+2^2+2^3+...+2^{2003}\)

\(2A-A=\left(2+2^2+2^3+...+2^{2003}\right)-\left(1+2+2^2+....+2^{2002}\right)\)

\(A=2^{2003}-1\)

Mà: \(2^{2003}=2^{2003}\)

\(\Rightarrow2^{2003}-1< 2^{2003}\)

\(\Rightarrow A< B\)

cuối bảng Tuyên ngôn Độc Lập,Bác Hồ khẳng định:''Nước Việt Nam có quyền hưởng tự do và độc lập và sự thật đã thành một nước tự do độc lập.Toàn thể dân tộc Việt Nam quyết đem tất cả tinh thần và lực lượng,tính mạng và của cải để giữ vững quyền tự do độc lập ấy.''

Cuối bản Tuyên ngôn độc lập, Bác Hồ thay mặt nhân dân Việt Nam khẳng định: “Nước Việt Nam có quyền hưởng tự do và độc lập, và sự thật thành một nước tự do, độc lập. Toàn thể dân tộc Việt Nam quyết đem tất cả tinh thần và lực lượng, tính mạng và của cải để giữ vững quyền tự do, độc lập ấy”.

Lời giải:

Đặt $\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk, c=dk$. Khi đó:

$\frac{a}{b}=\frac{bk}{b}=k(1)$

$\frac{a^2+c^2}{b^2+c^2}=\frac{(bk)^2+(dk)^2}{b^2+(dk)^2}=\frac{k^2(b^2+d^2)}{b^2+d^2k^2}(2)$

Từ $(1); (2)$ suy ra đề sai.

Do số học sinh của lớp 6A xếp thành:

Hàng 2 vừa đủ, hàng 3 vừa đủ, hàng 4 vừa đủ, hàng 8 vừa đủ 

Nên số học sinh của lớp 6A phải chia hết cho 2, 3, 4, 8 

⇒ Số học sinh lớp 6A ∈ BC(2, 3, 4, 8) 

Ta có: BCNN(2, 3, 4, 8) = 24 

⇒ Số học sinh lớp 6A ∈ {0; 24; 48; 72; ...} 

Mà số học sinh lớp 6A nằm trong khoảng từ 35 đến 60 

Nên số học sinh lớp 6A là 48 học sinh