Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x^2+1}{3x-13}\)<0
\(\Leftrightarrow\)x\(^2\)+1<0
\(\Leftrightarrow\)x\(^2\)<-1 (vô lí)
Vậy bất phương trình vô nghiệm
\(\dfrac{x^2+1}{3x-13}\)<0 ( x khác 13/3)
mà x2+1>0
=> 3x-13 <0
=> x<13/3

Gọi số học sinh giỏi năm 2018-2019 là \(x\)(học sinh) \(x\inℕ^∗\).
Số học sinh giỏi năm 2019-2020 là \(\left(1+15\%\right)x=1,15x\) (học sinh)
Vì tổng số học sinh giỏi hai năm là \(473\) nên ta có phương trình:
\(x+1,15x=473\)
\(\Leftrightarrow x=220\) (thỏa mãn)
Vậy số học sinh giỏi năm 2019-2020 là \(1,15.220=253\) học sinh.
Gọi số học sinh giỏi năm 2018-2019 là xx(học sinh) x∈N∗x∈ℕ∗.
Số học sinh giỏi năm 2019-2020 là (1+15%)x=1,15x(1+15%)x=1,15x (học sinh)
Vì tổng số học sinh giỏi hai năm là 473473 nên ta có phương trình:
x+1,15x=473x+1,15x=473
⇔x=220⇔x=220 (thỏa mãn)
Vậy số học sinh giỏi năm 2019-2020 là 1,15.220=2531,15.220=253 học sinh.

`Answer:`
1.
Ta có: `8=7+1=x+1`
\(B=x^{15}-8x^{14}+8x^{13}-...-8x^2+8x-5\)
\(=x^{15}-\left(x+1\right).x^{14}+\left(x+1\right).x^{13}-...-\left(x+1\right).x^2+\left(x+1\right).x-5\)
\(=x^{15}-x^{15}-x^{14}+x^{14}+x^{13}-...-x^3-x^2+x^2+x-5\)
\(=x-5\)
\(=7-5=2\)
2.
a. \(VP=a^3+3a^2b+3ab^2+b^3-3a^2b-3ab^2\)
\(=\left(a^3+b^3\right)+\left(3a^2b-3a^2b\right)+\left(3ab^2-3ab^2\right)\)
\(=a^3+b^3=VT\)
b. \(VT=a^3+b^3+c^3-3abc\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right).c+c^2\right]-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2+2ab-ac-bc-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=VP\)

\(3\left(x^2+x\right)^2+2\left(x^2+x\right)^2-1=0\)
Đặt \(\left(x^2+x\right)^2=a\)
pt⇔ \(3a+2a-1=0\)
\(\Leftrightarrow5a=1\)
\(\Leftrightarrow a=\dfrac{1}{5}\)
\(\Rightarrow\left(x^2+x\right)^2=\dfrac{1}{5}\)
\(\Rightarrow\left[{}\begin{matrix}x^2+x=\dfrac{1}{\sqrt{5}}\\x^2+x=-\dfrac{1}{\sqrt{5}}\end{matrix}\right.\)
Đến đây chuyển vế dùng delta là được

tôi có điều muốn tâm sự ai kb zalo với con VŨ PHƯƠNG MAI thì bảo nó rep tin nhắn tui nha hay có ny nên bỏ tui
<=> 3x<1-5
<=> 3x<-4
<=>x<\(\dfrac{-4}{3}\)
Vậy bất phương trình có nghiệm là x<\(\dfrac{-4}{3}\)
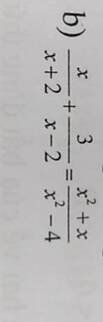
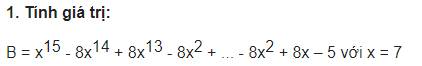
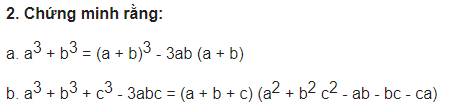
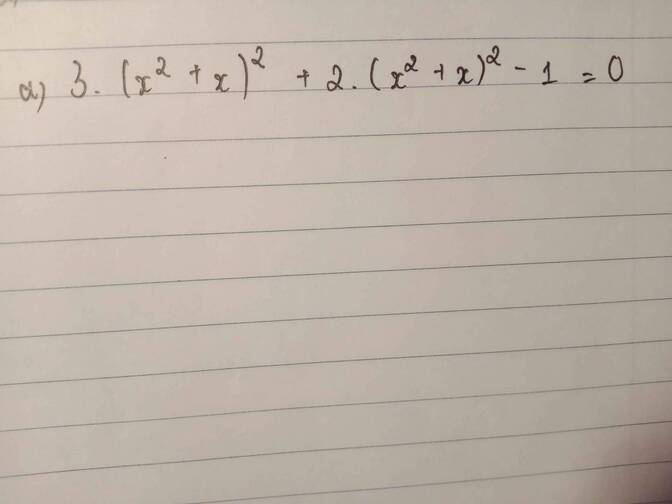
\(P=\left(\dfrac{a^2+2a}{a^3+2a^3+4a+8}+\dfrac{2}{a^2+4}\right)\div\dfrac{a^3-4a}{a^3-2a^2+4a-8}\)
\(=\left[\dfrac{a\left(a+2\right)}{\left(a+2\right)\left(a^2+4\right)}+\dfrac{2}{a^2+4}\right].\dfrac{\left(a-2\right)\left(a^2+4\right)}{a\left(a^2-4\right)}\)
\(=\dfrac{a+2}{a^2+4}.\dfrac{\left(a-2\right)\left(a^2+4\right)}{a.\left(a-2\right)\left(a+2\right)}=\dfrac{1}{a}\)