Ta có: l x+1l lớn hơn hoặc bằng 0, với mọi x

          l 2y -3l lớn hơn hoặc bằng 0, với mọi y

=> l x+1l + l 2y-3l lớn hơn hoặc bằng 0, với mọi x,y

=> l x+1l + l 2y-3l + 5 lớn hơn hoặc bằng 5

=> 1/ lx+1l + l2y-3l + 5 bé hơn hoặc bằng 1/5

=> 20/ lx+1l + l2y-3l+5 bé hơn hoặc bằng 20/5 = 4

Vậy max Q = 4

Dẫu "=" xảy ra <=> x = -1 ; y = 3/2

Chúc bạn học tốt!

Ta có: l x+1l lớn hơn hoặc bằng 0, với mọi x

          l 2y -3l lớn hơn hoặc bằng 0, với mọi y

=> l x+1l + l 2y-3l lớn hơn hoặc bằng 0, với mọi x,y

=> l x+1l + l 2y-3l + 5 lớn hơn hoặc bằng 5

=> 1/ lx+1l + l2y-3l + 5 bé hơn hoặc bằng 1/5

=> 20/ lx+1l + l2y-3l+5 bé hơn hoặc bằng 20/5 = 4

Vậy max Q = 4

Dẫu "=" xảy ra <=> x = -1 ; y = 3/2

a) Ta có: x²\(\ge0,\forall x\) 

=> x² +3/4 \(\ge\dfrac{3}{4}\) , mọi x

Vậy min A = 3/4

Dấu "=" xảy ra <=> x =0

b) ( x- 3/2)² -0,4

Ta có ( x-3/2)² lớn hơn hoặc bằng 0, mọi x

=> ( x-3/2)² - 0,4 lớn hơn hoặc bằng 0 - 0;4 = -0,4

Vậy min B =-0,4

Dấu "=" xảy ra <=> x = 3/2

Chúc bạn học tốt !

bạn cho mik hỏi là min A nghĩa là sao vậy

= -5/9 - 4/9 + 8/15 +7/15

= -1 + 1

= 0

\(\dfrac{-5}{9}\)-\(\left(\dfrac{8}{15}+\dfrac{4}{9}\right)\)+\(\dfrac{7}{15}\)=\(\left(\dfrac{-5}{9}-\dfrac{4}{9}\right)\)-\(\left(\dfrac{8}{15}-\dfrac{7}{15}\right)\)=-1-1/15=-16/15.

17+(-20)+23+(-26)+...+53+(-56)

=-3-3-3-...-3=-3x14=-52.

Bài 2:

a. $x^2=12y^2+1$ lẻ nên $x$ lẻ 

Ta biết một scp khi chia 8 dư $0,1,4$. Mà $x$ lẻ nên $x^2$ chia $8$ dư $1$

$\Rightarrow 12y^2+1\equiv 1\pmod 8$

$\Rightarrow 12y^2\equiv 0\pmod 8$

$\Rightarrow y^2\equiv 0\pmod 2$

$\Rightarrow y$ chẵn. Mà $y$ nguyên tố nên $y=2$.

Khi đó: $x^2=12y^2+1=12.2^2+1=49\Rightarrow x=7$ (tm)

Bài 2:

b.

$x^2=8y+1$ nên $x$ lẻ. Đặt $x=2k+1$ với $k$ tự nhiên.

Khi đó: $8y+1=x^2=(2k+1)^2=4k^2+4k+1$

$\Rightarrow 2y=k(k+1)$

Vì $(k,k+1)=1, k< k+1$ và $y$ nguyên tố nên xảy ra các TH sau:

TH1: $k=2, k+1=y\Rightarrow y=3\Rightarrow x=5$ (tm) 

TH2: $k=1, k+1=2y\Rightarrow y=1$ (vô lý) 

TH3: $k=y, k+1=2\Rightarrow y=1$ (vô lý)

Vậy $(x,y)=(5,3)$ là đáp án duy nhất thỏa mãn.

các thầy cô giúp em với ạ, em cảm ơn nhiều ạ:33

\(-12\cdot\left(x-5\right)+7\cdot\left(3-x\right)=5\\ -12\cdot x+60+21-7x=5\\ x\left(-12-7\right)+\left(60+21\right)=5\\ x\cdot\left(-19\right)+81=5\\ x\left(-19\right)=-76\\ x=4\)

$x+2/4-4/3=4x-1/12+2/3$

$x+1/2-4/3=4x-1/12+2/3$

$x-5/6=4x+7/12$

$-3x=5/6+7/12$

$-3x=17/12$

$x=17/12:(-3)$

$x=-17/36$

\(2x:\left(1+\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+...+\dfrac{1}{1+2+3+...x}\right)=2023\left(1\right)\)

Đặt \(A=\left(1+\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+...+\dfrac{1}{1+2+3+...x}\right)\)

\(\Rightarrow A=\left(1+\dfrac{1}{3}+\dfrac{1}{6}+...+\dfrac{1}{\dfrac{x\left(x+1\right)}{2}}\right)\)

\(\Rightarrow\dfrac{1}{2}A=\left(\dfrac{1}{2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{x\left(x+1\right)}\right)\)

\(\Rightarrow\dfrac{1}{2}A=\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{x}-\dfrac{1}{x+1}\right)\)

\(\Rightarrow\dfrac{1}{2}A=1-\dfrac{1}{x+1}\)

\(\Rightarrow A=2\left(1-\dfrac{1}{x+1}\right)\Rightarrow A=\dfrac{2x}{x+1}\)

\(\left(1\right)\Rightarrow2x:\dfrac{2x}{x+1}=2023\)

\(\Rightarrow2x.\dfrac{x+1}{2x}=2023\left(x\ne0\right)\)

\(\Rightarrow x+1=2023\)

\(\Rightarrow x=2022\)

Cần gấp

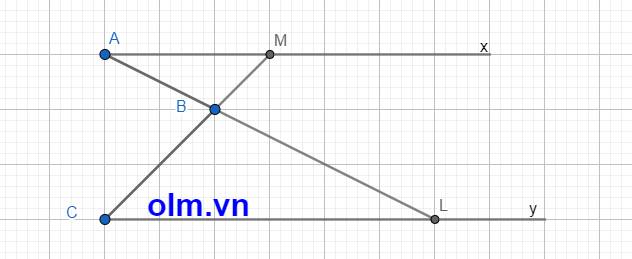
Để olm.vn giúp em, em nhé.

Kẻ AB kéo dài về phía B cắt đường thẳng y tại L

Kéo dài CB vế phía B cắt đường thẳng x tại M

Vì x//y ta có: \(\widehat{MAB}\)  = \(\widehat{BLC}\) ( so le trong)

                    \(\widehat{ABC}\)   =  \(\widehat{BCL}\) + \(\widehat{BLC}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)

                  ⇒ \(\widehat{ABC}\) = \(\widehat{BCL}\) + \(\widehat{MAB}\) (đpcm)

d, -(24 - 87) + (- 87 + 48 - 24)

  = - 24 + 87 - 87 + 48 - 24

= - (24 + 24) + (87 - 87 ) + 48

= -48 + 0 + 48

= 0

e, (2027. 2026²⁰²⁴ - 2026²⁰²⁴) : 2026²⁰²⁵

 =   2026²⁰²⁴.(2027 - 1):2026²⁰²⁵

=   2026²⁰²⁴.2026: 2026²⁰²⁵

= 2026²⁰²⁵:2026²⁰²⁵

= 1