ko bt

\(\left(x-1\right)^3+x^3+\left(x+1\right)^3=\left(x+2\right)^3\)

\(\Leftrightarrow x^3-3x^2+3x-1+x^3+x^3+3x^2+3x+1-x^3-6x^2-12x-8=0\)

\(\Leftrightarrow2x^3-6x^2-6x-8=0\)

\(\Leftrightarrow2.\left(x^3-3x^2-3x-4\right)=0\)

\(\Leftrightarrow x^3-4x^2+x^2-4x+x-4=0\)

\(\Leftrightarrow x^2.\left(x-4\right)+x.\left(x-4\right)+\left(x-4\right)=0\)

\(\Leftrightarrow\left(x-4\right).\left(x^2+x+1\right)=0\)

Mà \(x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)

\(\Rightarrow x-4=0\Leftrightarrow x=4\)

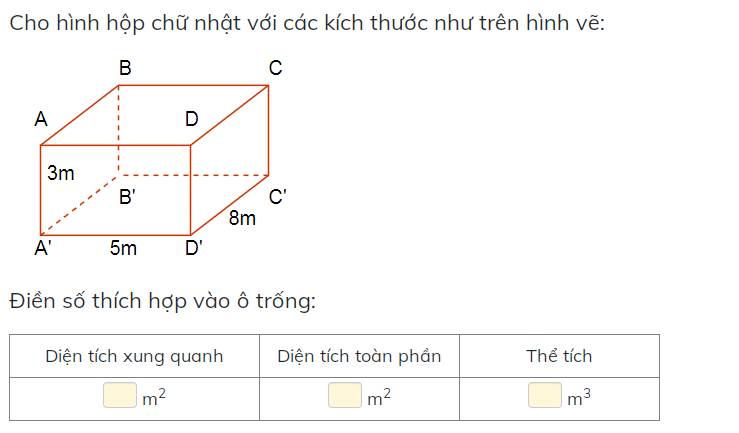
Lời giải:
Diện tích xung quanh: $2(3.5+3.8)=78$ (m²)

Diện tích toàn phần: $78+2.5.8=158$ (m²)

Thể tích: $3\times 5\times 8=120$ (m³)

Diện tích xung quanh là 78 m\(^2\).

Diện tích toàn phần là 158 m\(^2\).

Thể tích là 120 m\(^3\).

Điều kiện: \(x\ne1\)

\(\Leftrightarrow\dfrac{2}{x-1}-1>0\)

\(\Leftrightarrow\dfrac{2-x+1}{x-1}>0\)

\(\Leftrightarrow\dfrac{3-x}{x-1}>0\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}3-x>0\\x-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}3-x< 0\\x-1< 0\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< 3\\x>1\end{matrix}\right.\\\left\{{}\begin{matrix}x>3\\x< 1\end{matrix}\right.\end{matrix}\right.\)

\(\Rightarrow1< x< 3\)

\(\dfrac{4}{x+2}-\dfrac{1}{x}=\dfrac{x^2-2}{x^2+2x}\left(x\ne0;x\ne-2\right)\)

\(\Leftrightarrow\dfrac{4}{x+2}-\dfrac{1}{x}=\dfrac{x^2-2}{x\left(x+2\right)}\)

\(\Leftrightarrow\dfrac{4x-\left(x+2\right)}{x\left(x+2\right)}=\dfrac{x^2-2}{x\left(x+2\right)}\)

\(\Rightarrow4x-\left(x+2\right)=x^2-2\)

\(\Leftrightarrow4x-x-x^2=2-2\)

\(\Leftrightarrow3x-x^2=0\)

\(\Leftrightarrow x\left(3-x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(l\right)\\x=3\left(tm\right)\end{matrix}\right.\)

A B C E D I K

a/Xét tg vuông ABD và tg vuông ACE có \(\widehat{BAC}\) chung

=> tg ABD đồng dạng với tg ACE (g.g.g) 

\(\Rightarrow\dfrac{AE}{AD}=\dfrac{AC}{AB}\Rightarrow AE.AB=AD.AC\)

b/ Xét tứ giác BEDC có E và D cùng nhìn BC dưới 1 góc vuông

=> BEDC là tứ giác nội tiếp đường tròn đường kính BC

\(\Rightarrow\widehat{DEC}=\widehat{DBC}\) (góc nội tiếp cùng chắn cung DC) (1)

Ta có 

\(\widehat{AED}+\widehat{EDC}=\widehat{AEC}=90^o\) (2)

Xét tg vuông BCD có

\(\widehat{ACB}+\widehat{DBC}=90^o\) (3)

Từ (1) (2) (3) \(\Rightarrow\widehat{AED}=\widehat{ACB}\)

c/ Xét tg vuông IKE có KI=KE => tg IKE là tg vuông cân tại K

\(\Rightarrow\widehat{IEK}=\widehat{EIK}=45^o\)

\(\Rightarrow\widehat{IEK}=\widehat{BEK}+\widehat{IEB}=45^o\) (1)

Xét tg vuông BEC có

\(\widehat{BEK}=\widehat{ECB}\) (cùng phụ với \(\widehat{EBC}\) ) (2)

Ta có I và E cùng nhìn MC dưới 1 góc vuông => tứ giác MIEC là tứ giác nội tiếp đường tròn đường kính MC

\(\Rightarrow\widehat{IEB}=\widehat{BCM}\) (góc nội tiếp cùng chắn cung IM) (3)

Từ (1) (2) (3) \(\Rightarrow\widehat{BEK}+\widehat{IEB}=\widehat{ECB}+\widehat{BCM}=\widehat{ECM}=45^o\)

Xét tg vuông EMC

\(\widehat{EMC}=90^o-\widehat{ECM}=90^o-45^o=45^o=\widehat{ECM}\)

=> tg EMC cân tại E => EM=EC