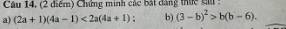
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left|2x+1\right|=3x-2\)đk : x >= 2/3
\(\left[{}\begin{matrix}2x+1=3x-2\\2x+1=2-3x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=\dfrac{1}{5}\left(ktm\right)\end{matrix}\right.\)

\(\dfrac{x\left(x-8\right)+3\left(x+6\right)}{\left(x+6\right)\left(x-8\right)}=\dfrac{-12x+33}{\left(x+6\right)\left(x-8\right)}\left(đk:x\ne-6;8\right)\)
\(x^2-8x+3x+18=-12x+33\)
\(x^2-5x+18+12x-33=0\)
\(x^2+7x+15=0\)
\(\text{∆}=7^2-4.15=-11< 0\)
⇒ pt vô nghiệm
đk : x khác -6 ; 8
\(x^2-8x+3x+18=-12x+33\Leftrightarrow x^2+7x-25=0\)
\(\Leftrightarrow x=\dfrac{-7\pm\sqrt{149}}{2}\)

b) +) |2x-3|=2x-3 khi 2x-3 ≥ 0 ⇔ x ≥ \(\dfrac{3}{2}\)
Khi đó PT b trở thành :
2x-3-x=5
⇔2x-x=5+3
⇔x=8 (tm)
+) |2x-3|=-2x+3 khi 2x-3 < 0 ⇔ x < \(\dfrac{3}{2}\)
Khi đó PT b trở thành :
-2x+3-x=5
⇔-2x-x=5-3
⇔-3x=2
⇔x=\(-\dfrac{2}{3}\) (tm)
vậy tập nghiệm của PT là S={8;\(-\dfrac{2}{3}\) }
a) kiểm tra xem có sai đề không bạn nhé
b) |2x-3|-x=5
|2x-3| =5+x
TH1: 2x-3 > 0 => x>3/2
=> 2x-3=5+x
=> x= 8 <t/m>
TH2 : 2x-3<0 => x<3/2
=> -2x+3=5+x
=> x =\(-\dfrac{3}{2}\)

Gọi chiều rộng ban đầu là \(a\left(a>0\right)\)
\(\Rightarrow\) Chiều rộng sau khi tăng thêm là \(a+20\)
\(\Rightarrow\) Chiều rộng ban đầu là \(170-a\)
\(\Rightarrow\) Chiều dài sau khi giảm đi là \(170-a-30=140-a\)
Nửa chu vi của khu đất là:
\(340:2=170m\)
Diện tích của khu đất ban đầu là \(a\left(170-a\right)=170a-a^2\)
Diện tích của khu đất lúc sau là \(\left(a+20\right)\left(140-a\right)=120a-a^2+2800\)
Do diện tích khu đất lúc sau tăng thêm \(600m^2\) nên ta có phương trình sau:
\(120a-a^2+2800-600=170a-a^2\)
\(\Leftrightarrow50a=2200\Leftrightarrow a=44\)
Vậy kích thước của khu đất là: \(a\left(170-a\right)=44.\left(170-a\right)=44.126=5544m^2\)
a) \(\left(2a+1\right)\left(4a-1\right)< 2a\left(4a+1\right)\)
\(\Leftrightarrow8a^2+4a-2a-1< 8a^2+2a\)
\(\Leftrightarrow8a^2+4a-2a-1-8a^2-2a< 0\)
\(\Leftrightarrow-1< 0\) (Luôn đúng với mọi \(a\))
b) \(\left(3-b\right)^2>b\left(b-6\right)\)
\(\Leftrightarrow9-6b+b^2>b^2-6b\)
\(\Leftrightarrow9-6b+b^2-b^2+6b>0\)
\(\Leftrightarrow9>0\) (Luôn đúng với mọi \(b\))