 Em nhờ các thầy cô giúp em ý thứ 4 ạ. Bài tập toán 9 ạ
Em nhờ các thầy cô giúp em ý thứ 4 ạ. Bài tập toán 9 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số sách ở ngăn thứ nhất lúc đầu là x (cuốn sách; \(x\in\mathbb{N}^*\))
Số sách ở ngăn thứ hai lúc đầu là: \(400-x\) (cuốn sách)
Số sách ở ngăn thứ nhất nếu chuyển đi 80 cuốn sách là: \(x-80\) (cuốn sách)
Số sách ở ngăn thứ hai nếu thêm 80 cuốn sách là: \(400-x+80=480-x\) (cuốn sách)
Vì sau khi chuyển sách, số sách ở ngăn thứ hai gấp 3 lần số sách ở ngăn thứ nhất nên ta có phương trình:
\(480-x=3\left(x-80\right)\)
\(\Leftrightarrow480-x=3x-240\)
\(\Leftrightarrow4x=720\)
\(\Leftrightarrow x=180\left(tm\right)\)
Khi đó, số sách ở ngăn thứ hai lúc đầu là: \(400-180=220\) (cuốn sách)
Vậy: ...

\(\left(x+2\right)\left(32-x+3\right)=x\left(32-x\right)+88\)
\(\left(x+2\right)\left(35-x\right)=-x^2+32x+88\)
\(-x^2+33x+70=-x^2+32x+88\)
\(70-88=32x-33x\)
\(x=18;y=14\)
Câu này mình làm đúng rồi nhưng lần sau mình trình bày đặt x, y ra sao, tại sao lại có biểu thức đó và đầu mỗi dòng mình nên có dấu tương đương nhé.

4. Gọi số chi tiết máy trong tháng thứ nhất mà tổ 1, tổ 2 sản xuất được lần lượt là \(x,y\) (chi tiết máy; \(x,y\in\mathbb{N}^*\))
Vì trong tháng thứ nhất, cả hai tổ sản xuất được 800 chi tiết máy nên ta có phương trình: \(x+y=800\) (1)
Số chi tiết máy tổ 1 sản xuất được trong tháng thứ hai là: \(x\left(100\%+15\%\right)=1,15x\) (chi tiết máy)
Số chi tiết máy tổ 2 sản xuất được trong tháng thứ hai là: \(y\left(100\%+20\%\right)=1,2y\) (chi tiết máy)
Vì trong tháng thứ hai, cả hai tổ đã sản xuất được 945 chi tiết máy nên ta có phương trình: \(1,15x+1,2y=945\) (2)
Từ (1) và (2) ta có hệ: \(\left\{{}\begin{matrix}x+y=800\\1,15x+1,2y=945\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=300\left(tm\right)\\y=500\left(tm\right)\end{matrix}\right.\)
Vậy trong tháng thứ nhất tổ 1 sản xuất được 300 sản phẩm, tổ 2 sản xuất được 500 sản phẩm.
5. Gọi số chiếc áo tổ thứ nhất, tổ thứ hai may được trong một ngày lần lượt là \(x,y\) (chiếc áo; \(x,y\in\mathbb{N}^*\))
Vì mỗi ngày tổ thứ hai may được nhiều hơn tổ thứ nhất 20 chiếc áo nên ta có phương trình: \(y-x=20\) (1)
Số chiếc áo tổ thứ nhất may được trong 7 ngày là: \(7x\) (chiếc)
Số chiếc áo tổ thứ hai may được trong 5 ngày là: \(5y\) (chiếc)
Vì nếu tổ thứ nhất may trong 7 ngày và tổ thứ hai may trong 5 ngày thì cả hai tổ may được 1540 chiếc áo nên ta có phương trình: \(7x+5y=1540\) (2)
Từ (1) và (2) ta có hệ: \(\left\{{}\begin{matrix}y-x=20\\7x+5y=1540\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=120\left(tm\right)\\y=140\left(tm\right)\end{matrix}\right.\)
Vậy trong một ngày tổ thứ nhất may được 120 chiếc áo; tổ thứ hai may được 140 chiếc áo.

Sửa đề: Cho ΔDEF đều
ΔDEF đều
=>\(\widehat{EFH}=60^0\)
=>\(sinEFH=sin60=\dfrac{\sqrt{3}}{2};cosEFH=cos60=\dfrac{1}{2}\)
\(tanEFH=tan60=\sqrt{3};cotEFH=cot60=\dfrac{1}{\sqrt{3}}\)
ΔDEF đều
mà EH là đường cao
nên EH là phân giác của góc DEF
=>\(\widehat{DEH}=30^0\)
=>\(sinDEH=sin30=\dfrac{1}{2};cosDEH=cos30=\dfrac{\sqrt{3}}{2}\)
\(tanDEH=tan30=\dfrac{1}{\sqrt{3}};cotDEH=cot30=\sqrt{3}\)

a) \(A=\left(\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\right)\cdot\dfrac{x-3\sqrt{x}}{x\sqrt{x}+1}\left(x\ne9;x\ne4;x\ge0\right)\)
\(=\left[\dfrac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}\right]\cdot\dfrac{x-3\sqrt{x}}{x\sqrt{x}+1}\)
\(=\left[\dfrac{2\sqrt{x}-9-x+9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}+\dfrac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\right]\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{-x+2\sqrt{x}+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}}{x-\sqrt{x}+1}\)
b) \(x=\sqrt{3+2\sqrt{2}}+\sqrt{11-6\sqrt{2}}+12\)
\(=\sqrt{\left(\sqrt{2}\right)^2+2\cdot\sqrt{2}\cdot1+1^2}+\sqrt{3^2-2\cdot3\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}+12\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}+\sqrt{\left(3-\sqrt{2}\right)^2}+12\)
\(=\sqrt{2}+1+3-\sqrt{2}+12\)
\(=16\)
Thay x=16 vào A ta có:
\(A=\dfrac{\sqrt{16}}{16-\sqrt{16}+1}=\dfrac{4}{16-4+1}=\dfrac{4}{13}\)
c) \(A=\dfrac{\sqrt{x}}{x-\sqrt{x}+1}\Rightarrow\dfrac{1}{A}=\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\)
\(\Rightarrow\dfrac{1}{A}=\dfrac{x}{\sqrt{x}}-\dfrac{\sqrt{x}}{\sqrt{x}}+\dfrac{1}{\sqrt{x}}=\sqrt{x}+\dfrac{1}{\sqrt{x}}-1\)
Vì \(\sqrt{x};\dfrac{1}{\sqrt{x}}>0\) nên áp dụng bđt cô si ta có:
\(\dfrac{1}{A}\ge2\sqrt{\sqrt{x}\cdot\dfrac{1}{\sqrt{x}}}-1=2-1=1\)
\(\Leftrightarrow A\le1\)
Dấu "=" xảy ra khi: \(\sqrt{x}=\dfrac{1}{\sqrt{x}}\Leftrightarrow x=1\)
Vậy: ...

Lời giải:
Áp dụng BĐT AM-GM:
$A=x(1-x^2)=x(1-x)(1+x)=(1+\sqrt{3})x.(2+\sqrt{3})(1-x)(1+x).\frac{1}{(\sqrt{3}+1)(\sqrt{3}+2)}$
$=(x+x\sqrt{3})[2+\sqrt{3}-(2+\sqrt{3})x](1+x).\frac{1}{(\sqrt{3}+1)(\sqrt{3}+2)}$
\(\leq \left[\frac{x+x\sqrt{3}+2+\sqrt{3}-(2+\sqrt{3})x+1+x}{3}\right]^3.\frac{1}{(1+\sqrt{3})(\sqrt{3}+2)}\\ =\frac{(\sqrt{3}+1)^3}{3\sqrt{3}}.\frac{1}{(\sqrt{3}+1)(\sqrt{3}+2)}=\frac{2}{3\sqrt{3}}\)
Vậy $A_{\max}=\frac{2}{3\sqrt{3}}$. Giá trị này đạt tại $x=\frac{1}{\sqrt{3}}$






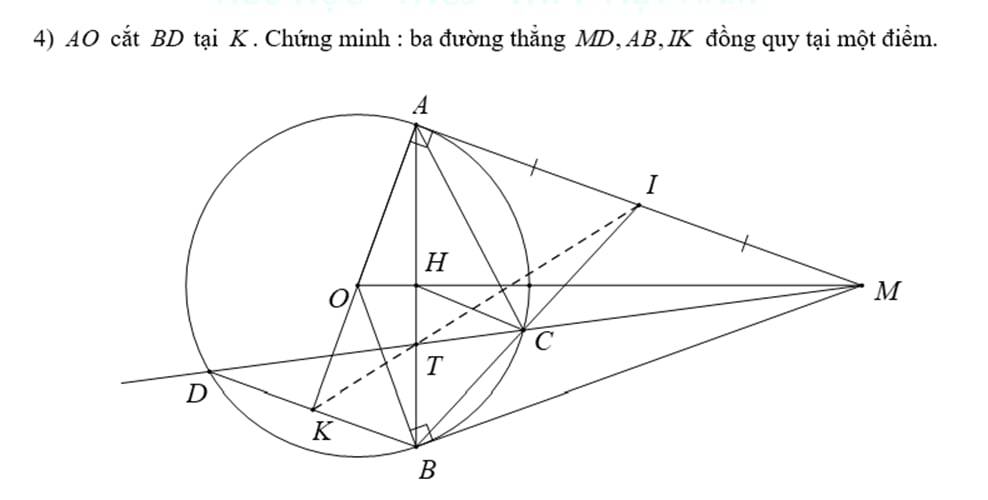
4)
Ta có:
AM // BD (cmt)
AO ⊥ AM (do MA là tiếp tuyến của (O) tại A)
⇒ AO ⊥ BD tại K
⇒ K là trung điểm của BD
Áp dụng định lý Thales đảo vào ∆AMT và ∆TBD, ta có:
⇒ ∆ATI ∽ ∆BTK (c-g-c)
⇒ ∠ATI = ∠BTK
⇒ ∠ATI và ∠BTK đối đỉnh
⇒ I, T, K thẳng hàng
⇒ T ∈ IK
⇒ MD, AB, IK đồng quy tại T