1) Gọi x (nghìn đồng) là giá niêm yết của áo kiểu A (x > 0)

Giá niêm yết áo kiểu B là: 900 - x (nghìn đồng)

Giá sau khi giảm của áo kiểu A: x - x.25% = 0,75x (nghìn đồng)

Giá sau khi giảm của áo kiểu B là:

900 - x - (900 - x).40% = (900 - x).0,6 = 540 - 0,6x (nghìn đồng)

Theo đề bài, ta có phương trình:

0,75x + 540 - 0,6x = 615

0,15x = 615 - 540

0,15x = 75

x = 75 : 0,15

x = 500 (nhận)

Vậy giá niêm yết của áo kiểu A là 500 nghìn đồng, giá niêm yết của áo kiểu B là 900 - 500 = 400 nghìn đồng

2) Diện tích xung quanh của chiếc hộp:

10 . 4 : 2 . 8 = 160 (cm²)

Bài 1:

Gọi chiều dài và chiều rộng mảnh đất lần lượt là $a$ và $b$ (m). ĐK: $a> b>0$

Theo bài ra ta có:

$a+b=100:2=50$

$(a+10)(b-5)=ab$

$\Leftrightarrow -5a+10b-50=0$

$\Leftrightarrow -a+2b=10$

$\Leftrightarrow a=2b-10$

Thay vào điều kiện $a+b=50$ thì:

$2b-10+b=50$

$3b-10=50$

$3b=60$

$b=20$ (m)

$a=50-b=50-20=30$ (m)

Bài 2:

Nửa chu vi hcn: $62:2=31$ (m) 

Chiều dài hcn: $(31+7):2=19$ (m) 

Chiều rộng hcn: $(31-7):2=12$ (m)

Diện tích hcn: $19.12=228$ (m²)

Em nên bình tĩnh, lúc này cần giữ an toàn tính mạng là trên hết. Nếu tên trộm chưa biết em cần tìm chỗ ẩn nấp, chờ tên trộm lấy xong đồ rồi bỏ đi. Nếu bị phát hiện em cần bình tĩnh tìm cơ hội để bỏ chạy và tìm người tới cứu.

a) x = 2 A = (2 - 6)/(2 + 2) = -1

b) B = 6/(x - 2) + x/(x + 2) - 8/(x² - 4)

= [6(x + 2) + x(x - 2) - 8]/[(x - 2)(x + 2)]

= (6x + 12 + x² - 2x - 8)/[(x - 2)(x + 2)]

= (x² + 4x + 4)/[(x - 2)(x + 2)]

= (x + 2)²/[(x - 2)(x + 2)]

= (x + 2)/(x - 2)

c) P = A.B

= (x - 6)/(x + 2) . (x + 2)/(x - 2)

= (x - 6)/(x - 2)

Để P = 2/3 thì

(x - 6)/(x - 2) = 2/3

3(x - 6) = 2(x - 2)

3x - 18 = 2x - 4

3x - 2x = -4 + 18

x = 14

Vậy x = 14 thì P = 2/3

\(4h25p=\dfrac{53}{12}\left(giờ\right)\)

Độ dài quãng đường từ nhà đến tỉnh là:

\(\dfrac{53}{12}\cdot14=\dfrac{371}{6}\left(km\right)\)

Gọi độ dài quãng đường từ Củ Chi đến Vũng Tàu là x(km)

(Điều kiện: x>0)

Thời gian đi là \(\dfrac{x}{40}\left(giờ\right)\)

Thời gian về là \(\dfrac{x}{40+10}=\dfrac{x}{50}\left(giờ\right)\)

Thời gian đi nhiều hơn thời gian về 27p=0,45 giờ nên ta có:

\(\dfrac{x}{40}-\dfrac{x}{50}=0,45\)

=>\(\dfrac{x}{200}=0,45\)

=>\(x=200\cdot0,45=90\left(nhận\right)\)

Vậy: Độ dài quãng đường từ Củ Chi đến Vũng Tàu là 90km

\(A-B=2.2^{n+1}=2^{n+2}\) là 1 lũy thừa của 2 nên ko chia hết cho 5

\(\Rightarrow A;B\) ko thể đồng thời chia hết cho 5

\(\Rightarrow\) Trong 2 số A, B có tối đa 1 số chia hết cho 5

Do \(16\equiv1\left(mod5\right)\) nên:

TH1: \(n=4k\Rightarrow\left\{{}\begin{matrix}2^{2n+1}=2^{8k+1}=2.\left(16\right)^{2k}\\2^{n+1}=2^{4k+1}=2.\left(16\right)^k\end{matrix}\right.\)

Do \(A=2.\left(16\right)^{2k}+2.\left(16\right)^k+1\equiv2+2+1\left(mod5\right)\equiv0\left(mod5\right)\)

\(\Rightarrow A\) chia hết cho 5 (và hiển nhiên, theo cm ban đầu B sẽ ko chia hết cho 5)

TH2: \(n=4k+1\Rightarrow\left\{{}\begin{matrix}2^{2n+1}=2^{8k+3}=8.\left(16\right)^{2k}\\2^{n+1}=2^{4k+2}=4.\left(16\right)^k\end{matrix}\right.\)

\(\Rightarrow B=8\left(16\right)^{2k}-4.\left(16\right)^k+1\equiv8-4+1\left(mod5\right)\equiv0\left(mod5\right)\)

\(\Rightarrow B\) chia hết cho 5

TH3: \(n=4k+2\Rightarrow\left\{{}\begin{matrix}2^{2n+1}=2^{8k+5}=2.\left(16\right)^{2k+1}\\2^{n+1}=2^{4k+3}=8.\left(16\right)^k\end{matrix}\right.\)

\(B=2.\left(16\right)^{2k+1}-8.\left(16\right)^k+1\equiv2-8+1\left(mod5\right)\equiv0\left(mod5\right)\)

\(\Rightarrow B\) chia hết cho 5

TH4: \(n=4k+3\Rightarrow\left\{{}\begin{matrix}2^{2n+1}=2^{8k+7}=8.\left(16\right)^{2k+1}\\2^{n+1}=\left(16\right)^{k+1}\end{matrix}\right.\)

\(\Rightarrow A=8.\left(16\right)^{2k+1}+\left(16\right)^{k+1}+1\equiv8+1+1\left(mod5\right)\equiv0\left(mod5\right)\)

\(\Rightarrow A\) chia hết cho 5

Vậy với mọi số tự nhiên n thì trong 2 số A và B luôn tồn tại 1 và chỉ 1 số chia hết cho 5

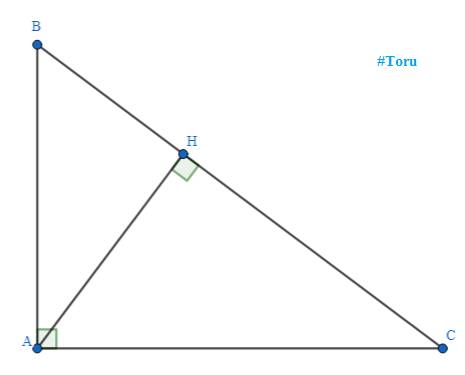
a, Xét \(\Delta HBA\) và \(\Delta ABC\) có:

\(\left\{{}\begin{matrix}\widehat{BHA}=\widehat{BAC}=90^{\circ}\left(AH\bot BC;\Delta ABC\text{ vuông tại }A\right)\\\widehat{ABC}\text{ chung}\end{matrix}\right.\)

\(\Rightarrow \Delta HBA\backsim \Delta ABC(g.g)\)

b, Vì \(\Delta HBA\backsim \Delta ABC(cmt)\Rightarrow \widehat{HAB}=\widehat{ACB}\) (hai góc tương ứng)

hay \(\widehat{HAB}=\widehat{HCA}\) (do \(H\in BC\)>)>

Xét \(\Delta AHB\) và \(\Delta CHA\) có: \(\left\{{}\begin{matrix}\widehat{AHB}=\widehat{CHA}=90^{\circ}\left(AH\bot BC\right)\\\widehat{HAB}=\widehat{HCA}\left(cmt\right)\end{matrix}\right.\)

\(\Rightarrow \Delta AHB\backsim \Delta CHA(g.g)\Rightarrow \dfrac{AH}{CH}=\dfrac{HB}{HA}\) (các cạnh tương ứng)

\(\Rightarrow AH^2=HB\cdot HC\)