Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
hình như đề bị sai rồi
\(\widehat{CAB}=\widehat{ACM}\) không thể là trung điểm BC được
a: Sửa đề: M là trung điểm của BC
Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>AE=AF
=>ΔAEF cân tại A
"Trái tim của chúng ta không chỉ là một cơ quan vật lý, mà còn là trung tâm của tâm hồn và cảm xúc. Nó đập liên tục, mang theo nhịp sống và hy vọng. Nuôi dưỡng trái tim ấm áp không chỉ là việc duy trì sức khỏe vật lý, mà còn là việc chăm sóc tâm hồn.
Khi ta nuôi dưỡng trái tim ấm áp, ta tạo ra một không gian cho tình thương, lòng nhân ái và sự kết nối. Đó là sự khả năng cảm nhận và chia sẻ niềm vui, nỗi buồn, và tình yêu với những người xung quanh. Trái tim ấm áp là nguồn động viên, giúp ta vượt qua khó khăn và thách thức trong cuộc sống.
Hãy dành thời gian để nghe trái tim mình, để cảm nhận những rung động và cảm xúc. Hãy trao đi những nụ cười, những lời chia sẻ, và những hành động nhỏ thể hiện tình thương. Và hãy nhớ rằng, trái tim ấm áp không chỉ là của riêng mình, mà còn là của tất cả mọi người."
a) Xét \(\Delta BAE\) và \(\Delta BDE\) có:
\(\left\{{}\begin{matrix}\widehat{BAE}=\widehat{BDE}=90^{\circ}\left(\Delta ABC\text{ vuông tại }A;DE\perp BC\right)\\BE\text{ chung}\\BA=BD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta BAE=\Delta BDE\left(ch-cgv\right)\) (đpcm)
b) Ta có: \(BD=BA\Rightarrow B\) là điểm nằm trên đường trung trực của AD (1)
Vì \(\Delta BAE=\Delta BDE\left(cmt\right)\Rightarrow AE=DE\) (2 cạnh tương ứng)
\(\Rightarrow E\) là điểm nằm trên đường trung trực của AD (2)
Từ (1) và (2) \(\Rightarrow BE\) là đường trung trực của AD
Mà: \(BE\cap AD=\left\{M\right\}\) nên \(BM\perp AD\)
hay \(BM\) là đường cao của \(\Delta ABD\) (đpcm)
c) Vì \(AE=DE\Rightarrow\Delta ADE\) cân tại E (t/c)
\(\Rightarrow\widehat{A_2}=\widehat{EDA}\) (t/c) (3)
Lại có: \(\begin{cases} AH\perp CD\\ DE\perp CD \end{cases} \Rightarrow AH//DE\)
\(\Rightarrow\widehat{A_1}=\widehat{EDA}\) (2 góc so le trong) (4)
Từ (3) và (4) \(\Rightarrow\widehat{A_1}=\widehat{A_2}\)
Mà tia AD nằm trong \(\widehat{HAC}\)
nên tia AD là tia phân giác của \(\widehat{HAC}\) (đpcm)
d) Xét \(\Delta EBC\) có: \(\left\{{}\begin{matrix}AB\perp EC\left(\Delta ABC\text{ vuông tại }A;E\in AC\right)\\DE\perp BC\left(gt\right)\\CF\perp BE\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow AB,DE,CF\) đồng quy (t/c) (đpcm)
$\text{#}Toru$
a: \(\dfrac{1}{2}< \dfrac{12}{a}< \dfrac{4}{3}\)
=>\(\dfrac{12}{24}< \dfrac{12}{a}< \dfrac{12}{9}\)
=>9<a<24
mà a nguyên
nên \(a\in\left\{10;11;...;23\right\}\)
b: \(\dfrac{7}{4}< \dfrac{a}{8}< 3\)
=>\(\dfrac{14}{8}< \dfrac{a}{8}< \dfrac{24}{8}\)
=>14<a<24
mà a nguyên
nên \(a\in\left\{15;16;...;23\right\}\)
c: \(\dfrac{2}{3}< \dfrac{a-1}{6}< \dfrac{8}{9}\)
=>\(\dfrac{12}{18}< \dfrac{3\left(a-1\right)}{18}< \dfrac{16}{18}\)
=>12<3a-3<16
=>15<3a<19
=>5<a<19/3
mà a nguyên
nên a=6
d: \(\dfrac{12}{9}< \dfrac{4}{a}< \dfrac{8}{3}\)
=>\(\dfrac{8}{6}< \dfrac{8}{2a}< \dfrac{8}{3}\)
=>3<2a<6
mà a nguyên
nên 2a=4
=>a=2
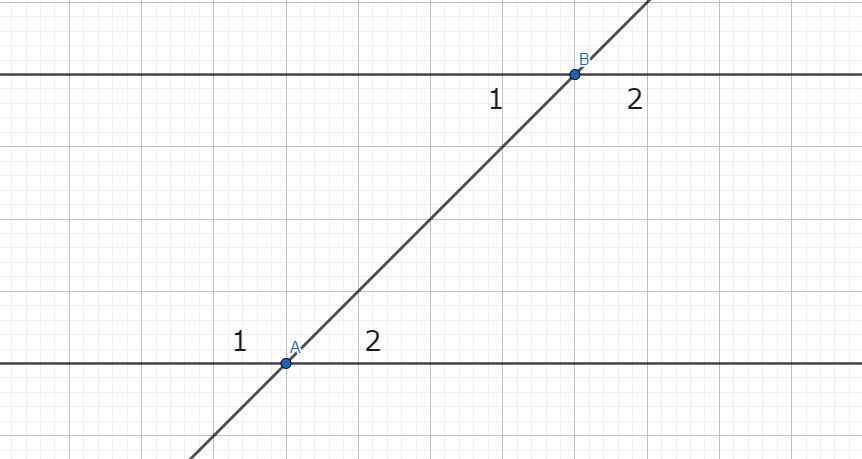Ta có: \(\widehat{A_1}=\widehat{B_2}\) (theo giả thiết)
Mặt khác:
\(\left\{{}\begin{matrix}\widehat{A_1}+\widehat{A_2}=180^o\\\widehat{B_1}+\widehat{B_2}=180^o\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A_1}=180^o-\widehat{A_2}\\\widehat{B_2}=180^o-\widehat{B_1}\end{matrix}\right.\) (hai cặp góc kề bù)
Mà \(\widehat{A_1}=\widehat{B_2}\) nên:
\(\widehat{A_2}=\widehat{B_1}\) Vậy nếu 1 đường thẳng cắt 2 đường thẳng mà trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì các cặp góc so le trong còn lại cũng bằng nhau.
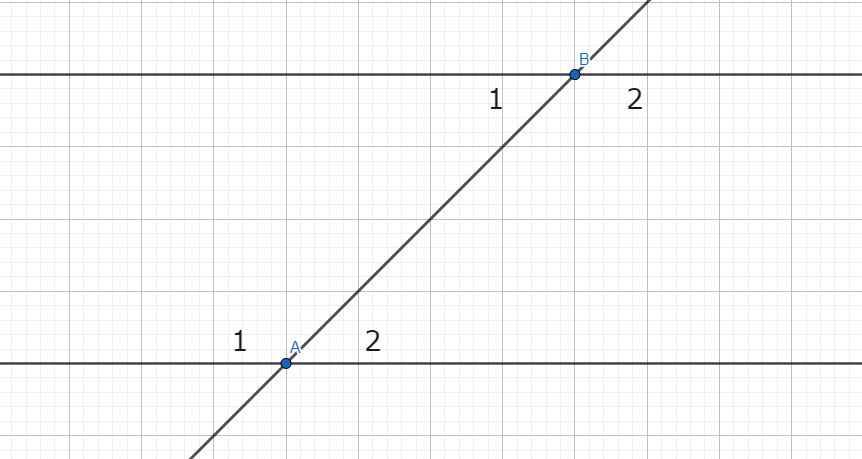Giả sử \(\widehat{A_1}\) và \(\widehat{B_2}\) là cặp góc so le trong đề bài cho.
Ta có: \(\widehat{A_1}=\widehat{B_2}\) (theo giả thiết)
Mặt khác:
\(\left\{{}\begin{matrix}\widehat{A_1}+\widehat{A_2}=180^o\\\widehat{B_1}+\widehat{B_2}=180^o\end{matrix}\right.\)(hai cặp góc kề bù)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A_1}=180^o-\widehat{A_2}\\\widehat{B_2}=180^o-\widehat{B_1}\end{matrix}\right.\)
Mà \(\widehat{A_1}=\widehat{B_2}\) nên:
\(\widehat{A_2}=\widehat{B_1}\) hay cặp góc so le trong còn lại bằng nhau
Vậy nếu 1 đường thẳng cắt 2 đường thẳng mà trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì cặp góc so le trong còn lại cũng bằng nhau.
`#3107.101107`
`1.`
Số hạng của tổng B:
`(99 - 1) \div 1 + 1 = 99` (số hạng)
Giá trị của tổng B:
`(99 + 1) \cdot 99 \div 2 = 4950`
Dấu âm đó là dấu âm của tử thôi bạn. Và vì mẫu số phải đáp ứng điều kiện là `<0` để là một phân số, nên nếu mẫu số có dấu âm sẽ được chuyển lên tử nhé! Nếu cả 2 đều chứa dấu âm thì phân số đó dương.
Ta có công thức luỹ thừa của một số hữu tỉ như sau:
(\(\dfrac{a}{b}\))m = \(\dfrac{a^m}{b^m}\) (a; b; m \(\in\) Z; b ≠ 0)
Áp dụng với ( \(\dfrac{-1}{2}\) )7 ta có a = -1; b = 2; m = 7
Khi đó: (\(\dfrac{-1}{2}\))7 = \(\dfrac{\left(-1\right)^7}{\left(2\right)^7}\) = \(\dfrac{-1}{128}\)
giup em bai nay em cam on
a:
Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>AE=AF
=>ΔAEF cân tại A