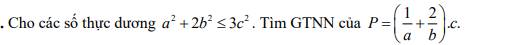
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


gọi số tuổi của Phương hiện tại là a (a ϵ N*)
gọi số tuổi của mẹ hiện tại là b (b ϵ N*)
ta có hiện tại tuổi mẹ gấp 3 lần tuổi Phương
→a=3b (1)
ta có 13 năm nữa tuổi mẹ gấp 2 lần tuổi Phương
→a+13=2(b+13)
→a+13=2b+26
→a=2b+13 (2)
từ (1) và (2) suy ra : 3b=2b+13
→b=13
vậy năm nay Phương 13 tuổi

\(\left(3x-1\right)^2-3\left(x-1\right)\left(x+3\right)\)
\(=9x^2-6x+1-3\left(x^2+2x-3\right)\)
\(=9x^2-6x+1-3x^2-6x+9\)
\(=6x^2-12x+10\)
\(=6\left(x^2-2x+\dfrac{10}{6}\right)\)
\(=6\left(x^2-2x.1+1-1+\dfrac{10}{6}\right)\)
\(=6\left[\left(x-1\right)^2+\dfrac{4}{6}\right]\)
\(=6\left(x-1\right)^2+4>0\forall x\inℝ\)
Vậy bất phương trình luôn đúng.

\(9x^2-6x+1-3\left(x^2+2x-3\right)\)
\(=6x^2-12x+10=6\left(x^2-2x+1-1\right)+10\)
\(\Leftrightarrow6\left(x-1\right)^2+4>0\)(luôn đúng)

\(\left(2x-1\right)\left(2x-3\right)\left(x+1\right)^2=18\)
\(\Leftrightarrow\left(2x-1\right)\left(2x-3\right)\left(2x+2\right)^2=72\) (*)
Đặt \(a=2x+2\)
(*) \(\Leftrightarrow\left(a-3\right)\left(a-5\right).a^2=0\)
\(\Leftrightarrow\left(a^3-5a^2\right)\left(a-3\right)=0\)
\(\Leftrightarrow a^4-8a^3+15a^2=0\)
\(\Leftrightarrow a^4-5a^3-3a^3+15a^2=0\)
\(\Leftrightarrow a^3.\left(a-5\right)-3a^2.\left(a-5\right)=0\)
\(\Leftrightarrow\left(a-5\right)\left(a-3\right).a^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\2x-1=0\\\left(2x+2\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{1}{2}\\x=-1\end{matrix}\right.\)

\(\left(2-3x\right)^2=\dfrac{1}{36}=\left(\dfrac{1}{6}\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}2-3x=\dfrac{1}{6}\\2-3x=-\dfrac{1}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{18}\\x=\dfrac{13}{18}\end{matrix}\right.\)
\(\left[{}\begin{matrix}2-3x=\dfrac{1}{6}\\2-3x=-\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=\dfrac{11}{6}\\3x=\dfrac{13}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{6}:3=\dfrac{11}{18}\\x=\dfrac{13}{6}:3=\dfrac{13}{18}\end{matrix}\right.\)

Áp dụng bất đẳng thức Cauchy Schwartz, ta được:
\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1^2}{a}+\dfrac{2^2}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\)
Áp dụng bất đẳng thức Cauchy Schwartz, ta được:
\(\left(a+2b\right)^2=\left(a.1+\sqrt{2}.\sqrt{2}b\right)^2\le\left(a^2+2b^2\right).3\)
\(\Rightarrow a+2b\le\sqrt{3\left(a^2+2b^2\right)}\le\sqrt{9c^2}=3c\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{2}{b}\ge\dfrac{9}{3c}=\dfrac{3}{c}\)
\(\Rightarrow P\ge\dfrac{3}{c}.c=3\)
Dấu "=" xảy ra khi \(a=b=c=1\)