a: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

=>\(\widehat{BAM}=\widehat{CAM}\)

Xét ΔAHM vuông tại H và ΔAKM vuông tại K có

AM chung

\(\widehat{HAM}=\widehat{KAM}\)

Do đó: ΔAHM=ΔAKM

=>MH=MK

b: Ta có: MH=MK

mà MK<MC(ΔMKC vuông tại K)

nên MH<MC

c: ΔKAM vuông tại K

=>AM là cạnh lớn nhất trong ΔKAM

=>MK<AM

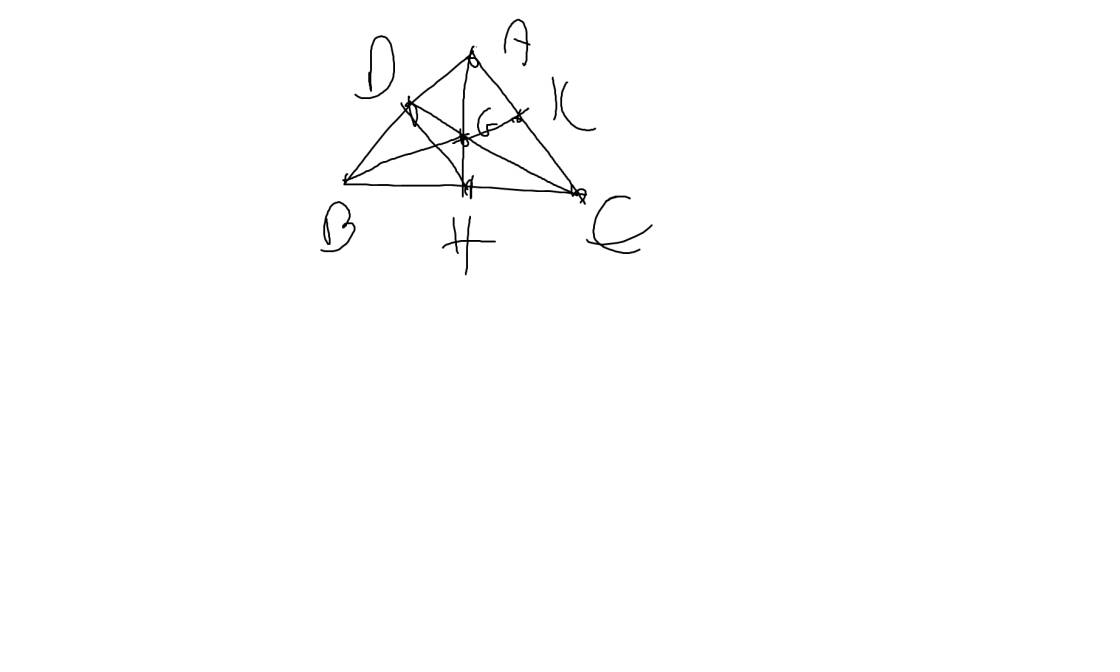
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

=>\(\widehat{HAB}=\widehat{HAC}\)

mà \(\widehat{DHA}=\widehat{HAC}\)(DH//AC)

nên \(\widehat{DHA}=\widehat{DAH}\)

=>ΔDAH cân tại D

b: Ta có: \(\widehat{DHA}+\widehat{DHB}=90^0\)

\(\widehat{DAH}+\widehat{DBH}=90^0\)

mà \(\widehat{DHA}=\widehat{DAH}\)(ΔDAH cân tại D)

nên \(\widehat{DHB}=\widehat{DBH}\)

=>DH=DB

=>DA=DB

=>D là trung điểm của AB

Xét ΔABC có

AH,CD là các đường trung tuyến

AH cắt CD tại G

Do đó: G là trọng tâm của ΔABC

c: Xét ΔABC có

G là trọng tâm

Do đó: BG cắt AC tại trung điểm K của AC

TA có: 

mà AB=AC

nên AD=DB=AK=KC

Xét ΔDBC và ΔKCB có

DB=KC

BC chung

Do đó: ΔDBC=ΔKCB

=>DC=BK

Xét ΔBAC có 

G là trọng tâm

BK là đường trung tuyến

Do đó: 

=>2BK=3BG

Trên tia đối của tia KB, lấy E sao cho KB=KE

Xét ΔKAE và ΔKCB có

KA=KC

(hai góc đối đỉnh)

KE=KB

Do đó: ΔKAE=ΔKCB

=>AE=CB 

AH+3BG=AH+2BK=AH+BE<AB+BE<(AB+AE+AB)=AB+AC+BC

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

=>\(\widehat{HAB}=\widehat{HAC}\)

mà \(\widehat{DHA}=\widehat{HAC}\)(DH//AC)

nên \(\widehat{DHA}=\widehat{DAH}\)

=>ΔDAH cân tại D

b: Ta có: \(\widehat{DHA}+\widehat{DHB}=90^0\)

\(\widehat{DAH}+\widehat{DBH}=90^0\)

mà \(\widehat{DHA}=\widehat{DAH}\)(ΔDAH cân tại D)

nên \(\widehat{DHB}=\widehat{DBH}\)

=>DH=DB

=>DA=DB

=>D là trung điểm của AB

Xét ΔABC có

AH,CD là các đường trung tuyến

AH cắt CD tại G

Do đó: G là trọng tâm của ΔABC

c: Xét ΔABC có

G là trọng tâm

Do đó: BG cắt AC tại trung điểm K của AC

TA có: \(AD=DB=\dfrac{AB}{2}\)

\(AK=KC=\dfrac{AC}{2}\)

mà AB=AC

nên AD=DB=AK=KC

Xét ΔDBC và ΔKCB có

DB=KC

\(\widehat{DBC}=\widehat{KCB}\)

BC chung

Do đó: ΔDBC=ΔKCB

=>DC=BK

Xét ΔBAC có 

G là trọng tâm

BK là đường trung tuyến

Do đó: \(\dfrac{BG}{BK}=\dfrac{2}{3}\)

=>2BK=3BG

Trên tia đối của tia KB, lấy E sao cho KB=KE

Xét ΔKAE và ΔKCB có

KA=KC

\(\widehat{AKE}=\widehat{CKB}\)(hai góc đối đỉnh)

KE=KB

Do đó: ΔKAE=ΔKCB

=>AE=CB 

AH+3BG=AH+2BK=AH+BE<AB+BE<(AB+AE+AB)=AB+AC+BC

a) Góc EAF là góc giữa hai đường trung trực của AB và AC. Do đó, góc EAF sẽ bằng 180o - góc A = 180^o - 100^o = 80^o.

b) Để chứng minh AO là tia phân giác của góc EAF, ta cần chứng minh rằng góc EAO = góc FAO.

Ta biết rằng góc EAO = góc BAO = \(\dfrac{1}{2}\) góc BAC = \(\dfrac{1}{2}\cdot\) 100^o = 50^o (vì AO là đường trung trực của AB).
Tương tự, góc FAO = góc CAO = \(\dfrac{1}{2}\) góc CAB = \(\dfrac{1}{2}\cdot\) 100^o = 50^o (vì AO là đường trung trực của AC).
Vì góc EAO = góc FAO, nên AO là tia phân giác của góc EAF.

hơi sai sai

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có

BE chung

BA=BD

Do đó: ΔBAE=ΔBDE

b: Xét ΔBFC có

FD,CA là các đường cao

FD cắt CA tại E

Do đó: E là trực tâm của ΔBFC

=>BE\(\perp\)FC

mà BE\(\perp\)BG

nên FC//BG

Ai giúp vs

Thể tích bể:

200 . 20 = 4000 (l) = 4 (m³)

Chiều dài của bể:

0,8 . 2 = 1,6 (m)

Chiều cao của bể:

4 : 0,8 : 1,6 = 3,125 (m) ≈ 3,1 (m)

Lời giải:

Chiều dài bể nước: $0,8\times 2=1,6$ (m) 

Thể tích của bể: 

$200\times 20=4000$ (lít)

Đổi $4000$ lít = $4$ m³

Chiều cao của bể:

$4:0,8:1,6=3,1$ (m)

Đề không đầy đủ. Bạn xem lại nhé.

a: Xét ΔABD và ΔAMD có

AB=AM

\(\widehat{BAD}=\widehat{MAD}\)

AD chung

Do đó: ΔABD=ΔAMD

b: Ta có: ΔABD=ΔAMD

=>DB=DM

=>D nằm trên đường trung trực của BM(1)

Ta có: AB=AM

=>A nằm trên đường trung trực của BM(2)

Từ (1),(2) suy ra AD là đường trung trực của BM

=>AD\(\perp\)BM tại I và I là trung điểm của BM

c: Xét ΔKMP và ΔKAB có

KM=KA

\(\widehat{MKP}=\widehat{AKB}\)(hai góc đối đỉnh)

KP=KB

Do đó: ΔKMP=ΔKAB

=>\(\widehat{KMP}=\widehat{KAB}\)

=>MP//AB

a: Xét ΔABD vuông tại A và ΔABE vuông tại A có

AB chung

AD=AE

Do đó: ΔABD=ΔABE

=>BD=BE

BE là phân giác của góc ABC

=>\(\widehat{ABE}=\widehat{CBE}=\dfrac{\widehat{ABC}}{2}=30^0\)

ΔAEB vuông tại A

=>\(\widehat{AEB}+\widehat{ABE}=90^0\)

=>\(\widehat{AEB}+30^0=90^0\)

=>\(\widehat{AEB}=60^0\)

Xét ΔBDE có BD=BE và \(\widehat{BED}=60^0\)

nên ΔBDE đều

b: ΔBAE=ΔBAD

=>\(\widehat{EBA}=\widehat{DBA}=30^0\)

\(\widehat{DBC}=\widehat{DBA}+\widehat{ABC}=30^0+60^0=90^0\)

=>BD\(\perp\)BC

c: ΔEBC cân tại E

mà EK là đường cao

nên K là trung điểm của BC

=>KB=KC

d: Xét ΔBFC có

FK,CA là các đường cao

FK cắt CA tại E

Do đó: E là trực tâm của ΔBFC

=>BE\(\perp\)CF

ΔABC cân tại A

mà AD là đường trung tuyến

nên AD\(\perp\)BC

Xét ΔADB vuông tại D có DE là đường cao

nên \(DE\cdot AB=DA\cdot DB\)

\(\left(DE+AB\right)^2-\left(DA+DB\right)^2\)

\(=DE^2+AB^2+2\cdot DE\cdot AB-DA^2-DB^2-2\cdot DA\cdot DB\)

\(=DE^2+\left(AB^2-AB^2\right)=DE^2>0\)

=>\(\left(DE+AB\right)^2>\left(DA+DB\right)^2\)

=>DE+AB>DA+DB