\(3x+6xy+2y=7\)

\(\Leftrightarrow3x+6xy+1+2y=8\)

\(\Leftrightarrow3x\left(1+2y\right)+\left(1+2y\right)=8\)

\(\Leftrightarrow\left(3x+1\right)\left(1+2y\right)=8\)

Do \(1+2y\) luôn lẻ với y nguyên nên ta chỉ cần xét các cặp ước của 8 mà \(1+2y\) nhận giá trị lẻ là \(-1;1\)

Vậy \(\left(x;y\right)=\left(-3;-1\right)\) là nghiệm duy nhất

\(12+15\times20\)

\(=12+300\)

\(=312\)

\(------\)

\(12\times20-20+38\)

\(=240-20+38\)

\(=220+38\)

\(=258\)

thịnh ngựa

Vẫn tuỳ thuộc vào điểm TBM cả năm em nhé

Gọi số cần tìm là \(abc4\).

Theo bài: \(abc4+2187=4abc\)

\(\Rightarrow10\cdot abc+4+2187=4000+abc\)

\(\Rightarrow9abc=1809\Rightarrow abc=201\)

Vậy số tự nhiên cần tìm là \(2014\)

Gọi số cần tìm là 
�
�
�
4
abc4.

Theo bài: 
�
�
�
4
+
2187
=
4
�
�
�
abc4+2187=4abc

⇒
10
⋅
�
�
�
+
4
+
2187
=
4000
+
�
�
�
⇒10⋅abc+4+2187=4000+abc

⇒
9
�
�
�
=
1809
⇒
�
�
�
=
201
⇒9abc=1809⇒abc=201

Vậy số tự nhiên cần tìm là 
2014
 

a,

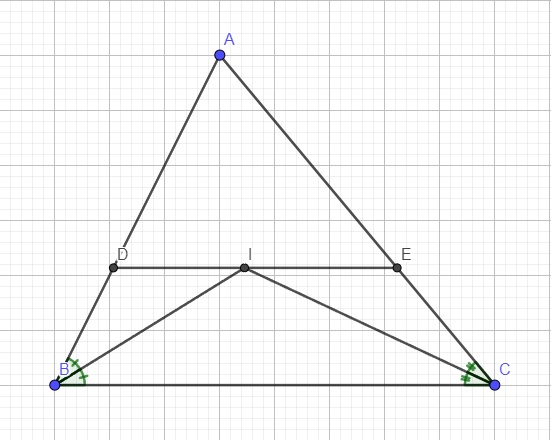
Do \(DE||BC\) (gt) \(\Rightarrow BDEC\) là hình thang

Do \(DE||BC\Rightarrow DI||BC\Rightarrow BDIC\) là hình thang

Do \(DE||BC\Rightarrow IE||BC\Rightarrow BIEC\) là hình thang

b.

Do \(DI||BC\Rightarrow\widehat{CBI}=\widehat{BID}\) (so le trong)

Mà \(\widehat{CBI}=\widehat{DBI}\) (do BI là phân giác góc B)

\(\Rightarrow\widehat{DBI}=\widehat{BID}\)

\(\Rightarrow\Delta BDI\) cân tại D

Tương tự ta có \(\widehat{ICB}=\widehat{CIE}\) (so le trong) và \(\widehat{ICB}=\widehat{ICE}\) (do IC là phân giác góc C)

\(\Rightarrow\widehat{CIE}=\widehat{ICE}\Rightarrow\Delta IEC\) cân tại E

c.

Từ câu b, do \(\Delta BDI\) cân \(\Rightarrow DB=DI\)

Do \(\Delta IEC\) cân \(\Rightarrow IE=CE\)

\(\Rightarrow BD+CE=DI+IE=DE\left(đpcm\right)\)

Gọi số cần tìm là \(x\left(đk:x\inℕ^∗\right)\)(\(x\) nguyên tố):

\(40⋮x\)

\(56⋮x\)

\(x\) nguyên tố

\(\Rightarrow x\inƯC\left(40,56\right)\)

⇒ Ta có:

\(40=2^3.5\)

\(56=2^3.7\)

\(\RightarrowƯCLN\left(40,56\right)=2^3=8\)

\(\RightarrowƯC\left(40,56\right)=Ư\left(8\right)=\left\{1;2;4;8\right\}\)

⇒ Mà x là số nguyên tố ⇒ \(x=2\)

⇒ Vậy số x cần tìm là 2.

Gọi số cần tìm là �(đ�:�∈N∗)x(đk:x∈N∗)($x$ nguyên tố):

$40⋮x$

$56⋮x$

$x$ nguyên tố

$\Rightarrow x\in ƯC\left(40,56\right)$

⇒ Ta có:

40=23.540=23.5

56=23.756=23.7

⇒Ư���(40,56)=23=8⇒ƯCLN(40,56)=23=8

$\Rightarrow ƯC\left(40,56\right)=Ư\left(8\right)=\left\{1;2;4;8\right\}$

⇒ Mà x là số nguyên tố ⇒ $x=2$

⇒ Vậy số x cần tìm là 2.

Ta có: 0,4=2/5

Hiệu số phần bằng nhau: 5-2=3(phần)

Hiệu mẫu số với tử số: 30 + 30 = 60

Mẫu số: 60 : 3 x 5 = 150

Tử số: 150 - 60 = 90

Phân số cần tìm: 90/150

Đ.số:.....

             0,4 = \(\dfrac{2}{5}\)

 Vì chuyển 30 đơn vị từ mẫu số lên tử số thì được phân số mới có giá trị bằng 1 nên mẫu số hơn tử số là 

             30 + 30 = 60

 Ta có sơ đồ: 

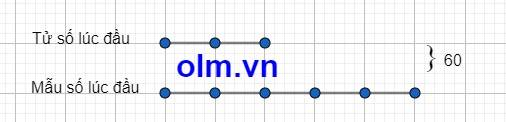
 Theo sơ đồ ta có:

             Tử số ban đầu: 60 : (5 - 2) x 2 = 40 

             Mẫu số ban đầu là:  40 + 60 = 100

             Phân số cần tìm là:  \(\dfrac{40}{100}\)  

Đặt \(n^2-3n=m^2\) với \(m\in N\)

\(\Rightarrow4n^2-12n=4m^2\)

\(\Rightarrow4n^2-12n+9=4m^2+9\)

\(\Rightarrow\left(2n-3\right)^2-\left(2m\right)^2=9\)

\(\Rightarrow\left(2n-3-2m\right)\left(2n-3+2m\right)=9\)

Vậy \(n=\left\{0;3;4\right\}\) là các giá trị thỏa mãn

   (-652) - {(-547) - 352 - [ (-147) - (-735) + (2200 + 65)]}

=  (-652)  + 547 + 352 - 147 - 735 - 2200 - 65

=  - (652 - 352) + (547 - 147) - (735 + 65) - 2200

=  - 300 + 400 - 1000 - 2200

=   100 - (1000 + 2200)

= 100 - 3200

= 3100

(-652) - {(-547) - 352 - [(-147) - (-735) + (2200 + 65)]}

= (-652) - {(-547) - 352 - [(-147) + 735 + 2265]}

= (-652) - {(-547) - 352 - [588 + 2265]}

= (-652) - {(-547) - 352 - 2853}

= (-652) - {(-899) - 2853}

= (-652) - (-3752)

= (-652) + 3752

= 3100

$\iff -4n+3⋮n+1$

$\iff -4n-4+7⋮n+1$

$\iff n+1\in \left\{1;7\right\}$

hay $n\in \left\{0;6\right\}$

$\iff -4n+3⋮n+1$

$\iff -4n-4+7⋮n+1$

$\iff n+1\in \left\{1;7\right\}$

hay $n\in \left\{0;6\right\}$