Ai giúp mình vs. Mình cần gấp!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TL:
Một con mèo vs thằng hói ai dz hơn?
Kết quả: Vé Báo Cáo dz hơn
Chúc bạn được OLM khóa acc
Trả lời cho câu hỏi một con mèo hay một thằng hói ai dz hơn
Dễ.1 thằng khác đời chỉ bị ám ảnh 2 từ ''báo'' và cáo dz hơn.

Thay x = -1 vào hs y = 5x + 3 ta được : \(y=-5+3=-2\)
=> hs trên đi qua A(-1;-2)
Mà y = ( 2m - 3 )x + m - 1 cắt y = 5x + 3 tại A(-1;-2)
<=> -2 = 3 - 2m + m - 1 <=> -m = -4 <=> m = 4

\(4\sqrt{x+1}=x^2-5x+14\)(x \(\ge-1\))
<=> \(-\left(x+1\right)+4\sqrt{x+1}-4=x^2-6x+9\)
<=> \(-\left(\sqrt{x+1}-2\right)^2=\left(x-3\right)^2\)
<=> \(\left(x-3\right)^2+\left(\sqrt{x+1}-2\right)^2=0\)
<=> \(\hept{\begin{cases}x-3=0\\\sqrt{x+1}-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=3\\x+1=4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=3\\x=3\end{cases}}\Leftrightarrow x=3\)(tm)
Vậy x = 3 là nghiệm phương trình
\(4\sqrt{x+1}=x^2-5x+14\)
\(4\sqrt{x+1}-x-5=x^2-6x+9\)
HT
@@@@@@@@@@@@@

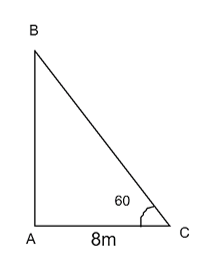
tanˆBCA=ABAC=AB8⇒tan600=AB8⇒AB=8√3(m)≈13,86mtan���^=����=��8⇒tan600=��8⇒��=83(�)≈13,86�
Vậy cây cổ thụ có chiều cao khoảng 13,86 m.

\(\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}\ge1+\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\)
\(\Leftrightarrow\)\(\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}-1-\left(a-b\right)^2-\left(b-c\right)^2-\left(c-a\right)^2\ge0\)
\(\Leftrightarrow\)\(\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}-a-b-c-\left(a-b\right)^2-\left(b-c\right)^2-\left(c-a\right)^2\ge0\)
\(\Leftrightarrow\frac{a^2}{b}-2a+b+\frac{b^2}{c}-2b+c+\frac{c^2}{a}-2c+a-\left(a-b\right)^2-\left(b-c\right)^2-\left(c-a\right)^2\ge0\)
\(\Leftrightarrow\)\(\frac{\left(a-b\right)^2}{b}-\left(a-b\right)^2+\frac{\left(b-c\right)^2}{c}-\left(b-c\right)^2+\frac{\left(c-a\right)^2}{a}-\left(c-a\right)^2\ge0\)
\(\Leftrightarrow\)\(\frac{\left(1-b\right)\left(a-b\right)^2}{b}+\frac{\left(1-c\right)\left(b-c\right)^2}{c}+\frac{\left(1-a\right)\left(c-a\right)^2}{a}\ge0\)(*)
Vậy ta phải chứng minh rằng \(\hept{\begin{cases}1-b\ge0\\1-c\ge0\\1-a\ge0\end{cases}}\)
Thật vậy, vì a,b,c>0 và a+b+c=1 nên ta có\(\hept{\begin{cases}b\le1\\c\le1\\a\le1\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}1-b\ge0\\1-c\ge0\\1-a\ge0\end{cases}}\)\(\Rightarrow\)(*) luôn đúng với a,b,c>0 và a+b+c=1.
Dấu "=" xảy ra \(\Leftrightarrow\)\(a=b=c=\frac{1}{3}\)
Vậy...

TL
ĐK: -4x + 5 ≥ 0 <=> x ≤ 5/4
Khi nào rảnh vào kênh H-EDITOR xem vid nha!!! Thanks!

