số tự nhiên x bé nhất sao cho x > 9,99
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Trong cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOt}< \widehat{xOy}\left(50^0< 120^0\right)\)
nên tia Ot nằm giữa hai tia Ox và Oy
=>\(\widehat{xOt}+\widehat{yOt}=\widehat{xOy}\)
=>\(\widehat{yOt}=120^0-50^0=70^0\)
b: Ta có: \(\widehat{xOy}+\widehat{x'Oy}=180^0\)(hai góc kề bù)
=>\(\widehat{x'Oy}=180^0-120^0=60^0\)
Ta có: \(\widehat{xOt}+\widehat{x'Ot}=180^0\)(hai góc kề bù)
=>\(\widehat{x'Ot}=180^0-50^0=130^0\)

a) ta có: \(B=\frac{n}{n-3}=\frac{n-3+3}{n-3}=\frac{n-3}{n-3}+\frac{3}{n-3}\)
Để B là số nguyên
\(\Rightarrow\frac{3}{n-3}\in z\)
\(\Rightarrow3⋮n-3\Rightarrow n-3\inƯ_{\left(3\right)}=\left(3;-3;1;-1\right)\)
nếu n -3 = 3 => n= 6 (TM)
n- 3 = - 3 => n = 0 (TM)
n -3 = 1 => n = 4 (TM)
n -3 = -1 => n = 2 (TM)
KL: \(n\in\left(6;0;4;2\right)\)
b) đề như z pải ko bn!
ta có: \(C=\frac{3n+5}{n+7}=\frac{3n+21-16}{n+7}=\frac{3.\left(n+7\right)-16}{n+7}=\frac{3.\left(n+7\right)}{n+7}-\frac{16}{n+7}=3-\frac{16}{n+7}\)
Để C là số nguyên
\(\Rightarrow\frac{16}{n+7}\in z\)
\(\Rightarrow16⋮n+7\Rightarrow n+7\inƯ_{\left(16\right)}=\left(16;-16;8;-8;4;-4;2;-2;1;-1\right)\)
rùi bn thay giá trị của n +7 vào để tìm n nhé ! ( thay như phần a đó)
a) ta có: \(B = \frac{n}{n - 3} = \frac{n - 3 + 3}{n - 3} = \frac{n - 3}{n - 3} + \frac{3}{n - 3}\)
Để B là số nguyên
\(\Rightarrow \frac{3}{n - 3} \in z\)
\(\Rightarrow 3 n - 3 \Rightarrow n - 3 \in Ư_{\left(\right. 3 \left.\right)} = \left(\right. 3 ; - 3 ; 1 ; - 1 \left.\right)\)
nếu n -3 = 3 => n= 6 (TM)
n- 3 = - 3 => n = 0 (TM)
n -3 = 1 => n = 4 (TM)
n -3 = -1 => n = 2 (TM)
KL: \(n \in \left(\right. 6 ; 0 ; 4 ; 2 \left.\right)\)
b) đề như z pải ko bn!
ta có: \(C = \frac{3 n + 5}{n + 7} = \frac{3 n + 21 - 16}{n + 7} = \frac{3. \left(\right. n + 7 \left.\right) - 16}{n + 7} = \frac{3. \left(\right. n + 7 \left.\right)}{n + 7} - \frac{16}{n + 7} = 3 - \frac{16}{n + 7}\)
Để C là số nguyên
\(\Rightarrow \frac{16}{n + 7} \in z\)
\(\Rightarrow 16 n + 7 \Rightarrow n + 7 \in Ư_{\left(\right. 16 \left.\right)} = \left(\right. 16 ; - 16 ; 8 ; - 8 ; 4 ; - 4 ; 2 ; - 2 ; 1 ; - 1 \left.\right)\)

\(\dfrac{3}{5}-\dfrac{1}{5}\cdot\left(x-\dfrac{1}{2}\right)=\dfrac{4}{5}\\ \dfrac{1}{5}\cdot\left(x-\dfrac{1}{2}\right)=\dfrac{3}{5}-\dfrac{4}{5}\\ \dfrac{1}{5}\cdot\left(x-\dfrac{1}{2}\right)=-\dfrac{1}{5}\\ x-\dfrac{1}{2}=-\dfrac{1}{5}:\dfrac{1}{5}\\ x-\dfrac{1}{2}=-1\\ x=-1+\dfrac{1}{2}\\ x=-\dfrac{1}{2}\)

\(\dfrac{3}{5}+\dfrac{4}{7}\times\dfrac{14}{6}\)
\(=\dfrac{3}{5}+\dfrac{56}{42}\)
\(=\dfrac{3}{5}+\dfrac{4}{3}=\dfrac{9}{15}+\dfrac{20}{15}=\dfrac{29}{15}\)

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

\(\frac{42}{54}\) = \(\frac{7}{x-1}\) (1 ≠ \(x\in Z\))
\(x-1\) = 7 : \(\frac{42}{54}\)
\(x-1\) = 9
\(x\) = 9 + 1
\(x=10\)
Vậy \(x=10\)
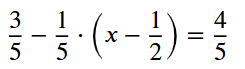


\(x>9,99\) nên \(x\in\left\{10,11,12,...\right\}\)
Mà x bé nhất nên \(x=10\)
10,00000000000..1