Tỉ số giữa số sách ở ngăn trên lúc đầu so với tổng số sách là \(\dfrac{1}{4+1}=\dfrac{1}{5}\)

Tỉ số giữa số sách ở ngăn trên lúc sau so với tổng số sách là \(\dfrac{1}{5+1}=\dfrac{1}{6}\)

Tổng số sách là \(4:\left(\dfrac{1}{5}-\dfrac{1}{6}\right)=4:\dfrac{1}{30}=120\left(quyển\right)\)

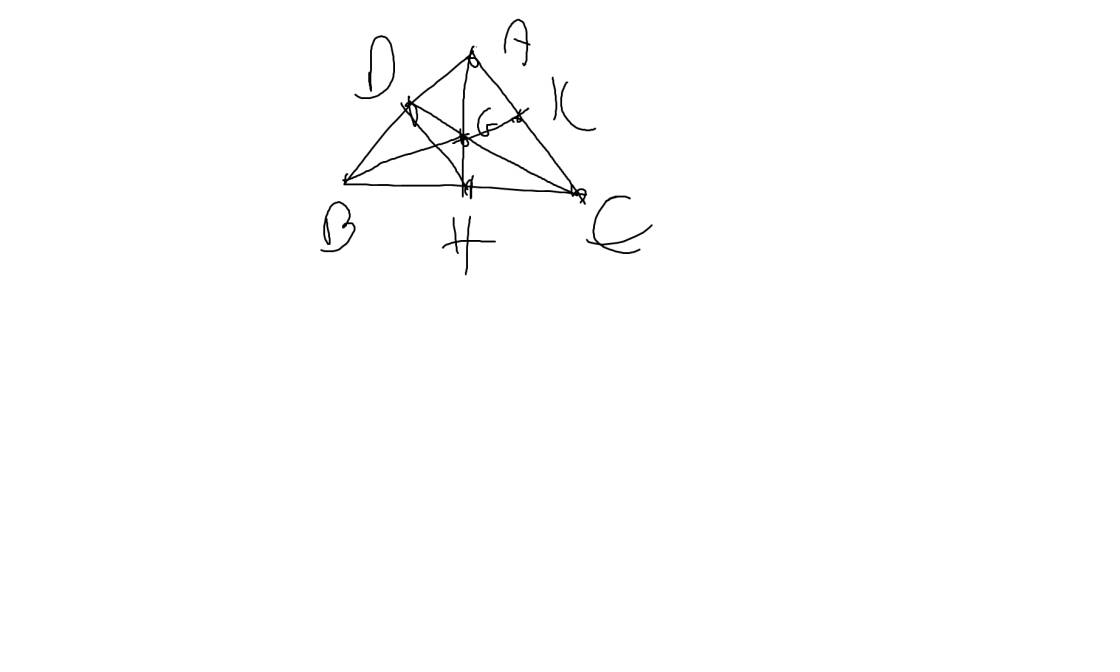
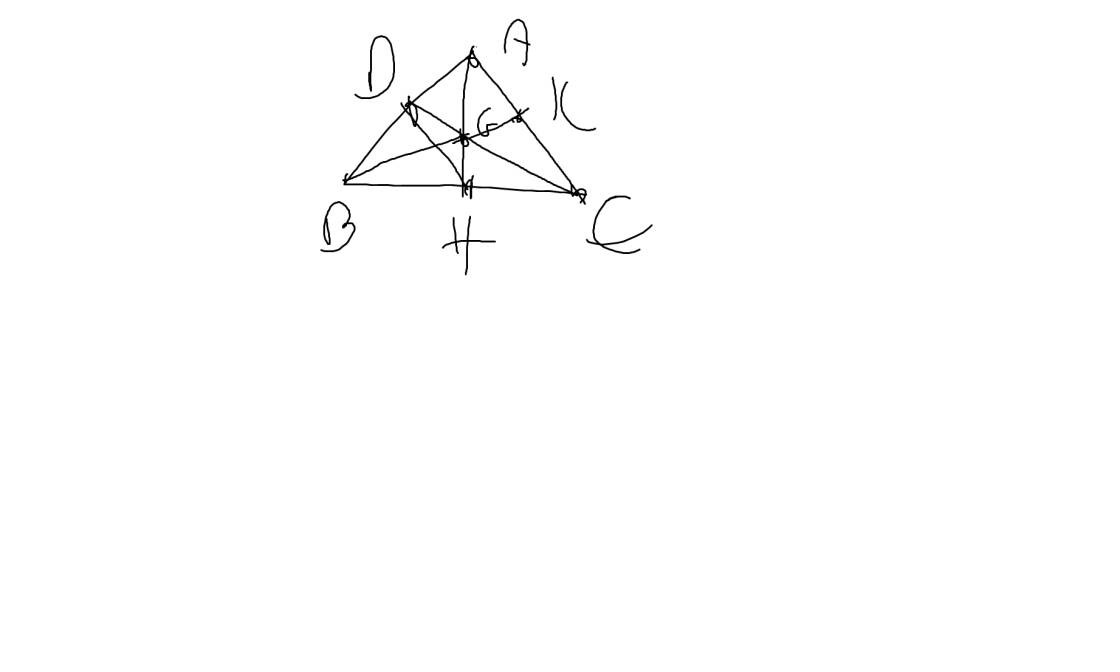
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

=>\(\widehat{HAB}=\widehat{HAC}\)

mà \(\widehat{DHA}=\widehat{HAC}\)(DH//AC)

nên \(\widehat{DHA}=\widehat{DAH}\)

=>ΔDAH cân tại D

b: Ta có: \(\widehat{DHA}+\widehat{DHB}=90^0\)

\(\widehat{DAH}+\widehat{DBH}=90^0\)

mà \(\widehat{DHA}=\widehat{DAH}\)(ΔDAH cân tại D)

nên \(\widehat{DHB}=\widehat{DBH}\)

=>DH=DB

=>DA=DB

=>D là trung điểm của AB

Xét ΔABC có

AH,CD là các đường trung tuyến

AH cắt CD tại G

Do đó: G là trọng tâm của ΔABC

c: Xét ΔABC có

G là trọng tâm

Do đó: BG cắt AC tại trung điểm K của AC

TA có: 

mà AB=AC

nên AD=DB=AK=KC

Xét ΔDBC và ΔKCB có

DB=KC

BC chung

Do đó: ΔDBC=ΔKCB

=>DC=BK

Xét ΔBAC có 

G là trọng tâm

BK là đường trung tuyến

Do đó: 

=>2BK=3BG

Trên tia đối của tia KB, lấy E sao cho KB=KE

Xét ΔKAE và ΔKCB có

KA=KC

(hai góc đối đỉnh)

KE=KB

Do đó: ΔKAE=ΔKCB

=>AE=CB 

AH+3BG=AH+2BK=AH+BE<AB+BE<(AB+AE+AB)=AB+AC+BC

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

=>\(\widehat{HAB}=\widehat{HAC}\)

mà \(\widehat{DHA}=\widehat{HAC}\)(DH//AC)

nên \(\widehat{DHA}=\widehat{DAH}\)

=>ΔDAH cân tại D

b: Ta có: \(\widehat{DHA}+\widehat{DHB}=90^0\)

\(\widehat{DAH}+\widehat{DBH}=90^0\)

mà \(\widehat{DHA}=\widehat{DAH}\)(ΔDAH cân tại D)

nên \(\widehat{DHB}=\widehat{DBH}\)

=>DH=DB

=>DA=DB

=>D là trung điểm của AB

Xét ΔABC có

AH,CD là các đường trung tuyến

AH cắt CD tại G

Do đó: G là trọng tâm của ΔABC

c: Xét ΔABC có

G là trọng tâm

Do đó: BG cắt AC tại trung điểm K của AC

TA có: \(AD=DB=\dfrac{AB}{2}\)

\(AK=KC=\dfrac{AC}{2}\)

mà AB=AC

nên AD=DB=AK=KC

Xét ΔDBC và ΔKCB có

DB=KC

\(\widehat{DBC}=\widehat{KCB}\)

BC chung

Do đó: ΔDBC=ΔKCB

=>DC=BK

Xét ΔBAC có 

G là trọng tâm

BK là đường trung tuyến

Do đó: \(\dfrac{BG}{BK}=\dfrac{2}{3}\)

=>2BK=3BG

Trên tia đối của tia KB, lấy E sao cho KB=KE

Xét ΔKAE và ΔKCB có

KA=KC

\(\widehat{AKE}=\widehat{CKB}\)(hai góc đối đỉnh)

KE=KB

Do đó: ΔKAE=ΔKCB

=>AE=CB 

AH+3BG=AH+2BK=AH+BE<AB+BE<(AB+AE+AB)=AB+AC+BC

C

c

Thuật toán hay giải thuật (tiếng anh là Algorithm) có khá nhiều định nghĩa phức tạp. Bạn có thể đọc ở nhiều nguồn để hiểu thêm về nó. Cá nhân tôi định nghĩa dễ hiểu rằng, thuật toán là “thuật” (phương pháp) để giải quyết 1 bài toán. Nói dễ hiểu hơn, mỗi một bài toán giống như một chiếc hòm chứa đựng kho báu (kết quả, đáp án), và chiếc chìa khoá để mở cái hòm đó chính là “giải thuật”. Nếu dùng sai chìa khoá, bạn vẫn có thể mở được hòm, nhưng mà sẽ mất nhiều thời gian, hoặc mở được hòm thì kho báu ở bên trong bị méo mó, không toàn vẹn. Sử dụng đúng chìa khoá, sẽ giúp bạn lấy được kho báu 1 cách dễ dàng, nhanh chóng. Tất nhiên mỗi chiếc hòm sẽ luôn cần loại chìa khoá khác nhau, giống như một bài toán luôn có những giải thuật xác định. Không có chiếc chìa khoá nào mở được tất cả các hòm, cũng như không có giải thuật nào giải được toàn bộ các bài toán.

BẠN THAM KHẢO DC CÁI NÀO THÌ VIẾT VÀO NHÉ !!!

thứ sáu

Thứ bảy

a) Góc EAF là góc giữa hai đường trung trực của AB và AC. Do đó, góc EAF sẽ bằng 180o - góc A = 180^o - 100^o = 80^o.

b) Để chứng minh AO là tia phân giác của góc EAF, ta cần chứng minh rằng góc EAO = góc FAO.

Ta biết rằng góc EAO = góc BAO = \(\dfrac{1}{2}\) góc BAC = \(\dfrac{1}{2}\cdot\) 100^o = 50^o (vì AO là đường trung trực của AB).
Tương tự, góc FAO = góc CAO = \(\dfrac{1}{2}\) góc CAB = \(\dfrac{1}{2}\cdot\) 100^o = 50^o (vì AO là đường trung trực của AC).
Vì góc EAO = góc FAO, nên AO là tia phân giác của góc EAF.

hơi sai sai