tìm giá trị nhỏ nhất của biểu thức
A= x^2 - 12x+ 30
B= 16x^2 + 40x+ 31
C= x^2- 15x + 60
D= x^2+ 17x + 75
E= 2x^2- 7x + 8
F= 3x^2+ 5x+ 6
K= 3x^2+ y^2+ 2xy = 12x +2040
L= 4x^2 +3y^2 - 4xy + 20y+2072
giúp vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(m^2+n^2=9m+13n-20\Leftrightarrow4m^2+4n^2=36m+52n-80\)
\(\Leftrightarrow\left(4m^2+36m+81\right)+\left(4n^2+52n+169\right)-170=0\)
\(\Leftrightarrow\left(2m+9\right)^2+\left(2n+13\right)^2=170\)
Vì \(\left(2n+13\right)^2\ge0\forall n\in z\)
\(\Rightarrow\left(2m+9\right)^2\le170\)
\(\Rightarrow\left(2m+9\right)^2=\left\{0;1;4;9;16;25;36;49;64;81;100;121;144;169\right\}\)
..... (Thay vào tìm m rồi tiếp tục tìm n. m, n là các số nguyên nên chú ý loại bớt trường hợp)

a) Gọi giao điểm của IM với AB là E; giao điểm của MD với BC là F
Xét \(\Delta BIE\) và \(\Delta BME:\)
BE: cạnh chung
\(\widehat{BEI}=\widehat{BEM}=90^o\)
IE=ME
=> \(\Delta BIE=\Delta BME\left(c-g-c\right)\)
=> BI=BM(1)
Chứng minh tương tự ta được \(\Delta BMF=\Delta BDF\left(c-g-c\right)\) BM=BD(2)
Từ (1) và (2) suy ra BI=BD
b) Vì \(\Delta BIE=\Delta BME\Rightarrow\widehat{IBE}=\widehat{MBE}\)
\(\Delta BMF=\Delta BDF\Rightarrow\widehat{MBF}=\widehat{DBF}\)
\(\Rightarrow\widehat{IBD}=\widehat{IBE}+\widehat{EBM}+\widehat{MBF}+\widehat{FBD}=2\widehat{EBM}+2\widehat{MBF}\)
\(=2\left(\widehat{EBM}+\widehat{MBF}\right)=2.60^o=120^o\)
Vậy \(\widehat{IBD}=120^o\)




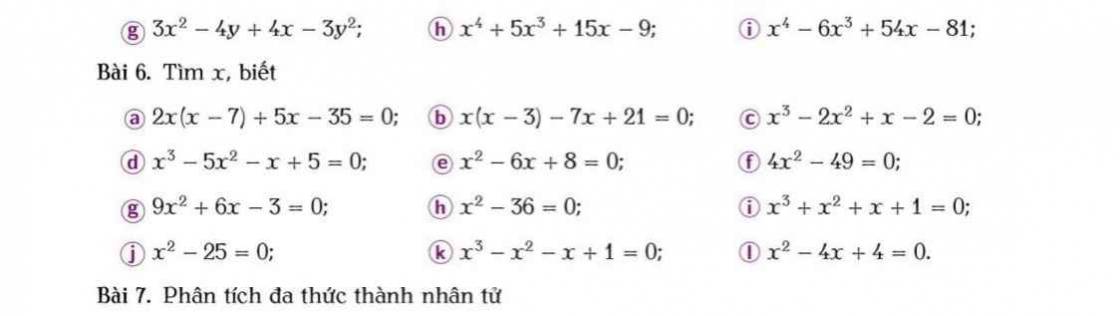
Lần sau bạn có thể tách nhỏ câu để dễ được giúp đỡ hơn nha
*Ta có: \(A=x^2-12x+30=x^2-12x+36-6\)
\(=\left(x-6\right)^2-6\ge-6\forall x\in R\)
Dấu ''='' xảy ra khi \(x=6\)
*Ta có: \(B=16x^2+40x+31=16x^2+40x+25+6\)
\(=\left(4x+5\right)^2+6\ge6\forall x\in R\)
Dấu ''='' xảy ra khi \(x=-\dfrac{5}{4}\)
*Ta có: \(C=x^2-15x+60=x^2-2.\dfrac{15}{2}x+\dfrac{225}{4}+\dfrac{15}{4}\)
\(=\left(x-\dfrac{15}{2}\right)^2+\dfrac{15}{4}\ge\dfrac{15}{4}\forall x\in R\)
Dấu ''='' xảy ra khi \(x=\dfrac{15}{2}\)
*Ta có: \(D=x^2+17x+75=x^2+2.\dfrac{17}{2}x+\dfrac{289}{4}+\dfrac{11}{4}\)
\(=\left(x+\dfrac{17}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\forall x\in R\)
Dấu ''='' xảy ra khi \(x=-\dfrac{17}{2}\)
*Ta có: \(E=2x^2-7x+8=2\left(x^2-\dfrac{7}{2}x+4\right)=2\left(x^2-2.\dfrac{7}{4}+\dfrac{49}{16}+\dfrac{15}{16}\right)\)
\(=2\left(x^2-2.\dfrac{7}{4}+\dfrac{49}{16}\right)+\dfrac{15}{8}=2\left(x-\dfrac{7}{4}\right)^2+\dfrac{15}{8}\ge\dfrac{15}{8}\forall x\in R\)
Dấu ''='' xảy ra khi \(x=\dfrac{7}{4}\)
*Ta có: \(F=3x^2+5x+6=3\left(x^2+\dfrac{5}{3}x+2\right)=3\left(x^2+2.\dfrac{5}{6}x+\dfrac{25}{36}+\dfrac{47}{36}\right)\)
\(=3\left(x+\dfrac{5}{6}\right)^2+\dfrac{47}{12}\ge\dfrac{47}{12}\forall x\in R\)
Dấu ''='' xảy ra khi \(x=-\dfrac{5}{6}\)
*Ta có: \(K=3x^2+y^2+2xy=12x+2040\) (Bạn xem lại đề có phải đánh sai ở chỗ dấu ''='' không nhé, chỗ đấy nếu là dấu cộng hay dấu trừ thì cũng làm theo cách này nha, thay mỗi dấu đi thôi á)
\(=2\left(x^2+6x+9\right)+\left(x^2+2xy+y^2\right)+2022\)
\(=2\left(x+3\right)^2+\left(x+y\right)^2+2022\ge2022\forall x\in R\)
Dấu ''='' xảy ra khi \(\left\{{}\begin{matrix}x+3=0\\x+y=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=3\end{matrix}\right.\)
*Ta có: \(L=4x^2+3y^2-4xy+20y+2072=\left(4x^2-4xy+y^2\right)+2\left(y^2+10y+25\right)+2022\)\(=\left(2x-y\right)^2+2\left(y+5\right)^2+2022\ge2022\forall x\in R\)
Dấu ''='' xảy ra khi \(\left\{{}\begin{matrix}2x-y=0\\y+5=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x=y\\y=-5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{5}{2}\\y=-5\end{matrix}\right.\)